车辆稳定控制技术液压理论模型与动力学模型解析

在稳控系统仿真平台的研究中，稳控系统液压制动系统模型是重点和难点之一，这里所指的稳控系统制动系统是包括HCU、主缸、轮缸、制动管路等在内的整套制动系统。由于受制动系统的零部件之间的间隙、制动元件的弹性以及摩擦等许多不确定性因素的影响，制动压力-力矩响应表现出死区、饱和、满环等非线性动态特性。整个制动系统的响应由准静态部分和瞬态部分构成。瞬态特性是指HCU的间歇式压力调节使制动管路压力产生急剧变化的特性，制动管路内制动液的流动状态、制动器的刚度特性等对制动器的瞬态特性具有重要的影响，动态特性的存在使制动力矩的建立滞后于制动压力。制动器的准静态特性是指在制动过程中，制动器摩擦系数随车轮转速、温度等变化而缓慢变化的特性。摩擦系数的变化造成制动压力与制动力矩间的非线性关系。动力学模型可以分为理论模型、半经验模型和经验模型等，液压制动系统包括制动主缸、HCU、制动管路和制动轮缸。驾驶人所施加的踏板力传递到制动主缸的活塞上，推动前、后缸两个活塞向前运动，将制动液压入制动管路。制动液通过HCU后，流经同制动硬管和制动软管组成的制动管路，进入制动轮缸。

HCU由增压阀、减压阀、蓄能器、回流泵和阻尼器组成，增压阀为常开阀，减压阀为常闭阀，每个制动轮缸都由一套独立的增、减压阀对自身的制动压力进行调节。稳控系统通过对电磁线圈施加控制信号来控制增压阀和减压阀的通断，以实现增压、保压和减压的防抱死控制过程：在增压阶段，增、减压阀上均无控制信号，增压阀打开，减压阀关闭，由制动主轴过来的制动液不能进入减压回路，而是通过增压阀阀口进入相应的制动管路，并经过制动软管进入制动轮缸，使制动压力不断升高。在保压阶段，只对增压阀施加电信号使其关闭，这样便切断了制动轮缸与制动主缸之间的联系，使其内部压力保持不变。在减压阶段，对增、减压阀同时施加电信号，增压阀关闭，减压阀打开，各制动轮缸与减压回路相连通，轮缸中的制动液便通过减压阀阀口进入弹簧活塞式蓄能器，实现制动压力的降低。蓄能器中的制动液会在回油泵的作用下随制动踏板的抬起排回制动主缸；如果稳控系统制动还未结束，制动液会在回油泵和增压阀之间聚积成一高压区域，等增压阀打开时再次进入轮缸。在回油泵和制动主缸之间，阻尼器起降低液压脉动和噪声的作用。

HCU模型包括增压阀、减压阀、阻尼器、蓄能器、回油泵几个部分。节流器模型在稳控系统液压制动系统中应用非常广泛，各组增压阀均有各自的节流器，各组减压阀在各自的隔磁管上均开有节流孔；阻尼器其本质也是一个节流器。因此HCU中的增压阀、减压阀和阻尼器均用节流器的动力学模型表示。在节流器的动力学模型中，输入量为制动液压力，输出为通过节流器的制动液流量。计算表达式如式（2-18）表示。

式中 Q——制动液流量；

C_q——流量系数；

ρ——制动液密度；

Δp——模型两端压力差；

A——节流孔截面积。

考虑到模型计算的精度，流量系数C_q不应当为一个恒定的值，引入式（2-19）和式（2-20）。

式中 D_h——阀直径；

λ——制动液流动雷诺数；

χ——节流孔湿周长度；

η——制动液动力黏度。

流量系数C_q的表达式如式（2-21）。

式中 C_qmax——最大流量系数；

λ_c——层流变紊流的临界雷诺数。

节流器动力学模型，如式（2-22）。

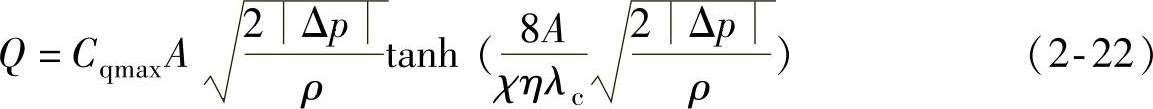
模型中考虑了流量系数的非恒定性，当Δp较小时，流量Q基本与Δp成正比，随着Δp的增大，流量系数很快接近于C_qmax，流量Q与√|Δp|成正比。这样，改变节流器的孔径即可得到不同的流量特性。HCU中的低压蓄能器为弹簧活塞式液压蓄能器。由于活塞的质量很轻，故建模时不考虑活塞惯性。HCU蓄能器模型输入量为制动液流量，输出量为制动液压力。模型的示意图如图2-23所示，S为活塞的最大行程，x为活塞瞬时的位置。

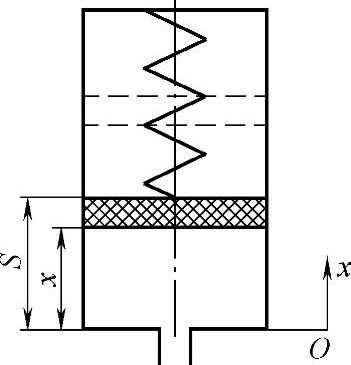
图2-23 蓄能器模型

由弹簧和活塞位置关系，可得：

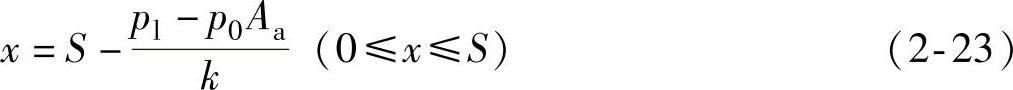
式中 p_l——活塞在最大行程时的弹簧力；

p₀——蓄能器内制动液压力；

A_a——活塞面积；

k——弹簧刚度。

式（2-33）两边对时间t求微分，结果如式（2-24）。

由于蓄能器为液容性元件，其考虑到活塞位移的基本方程如式（2-25）。

式中 K_y——制动液体积弹性模量；

V_a——蓄能器内制动液体积；

q₀——端口流量。

蓄能器动力学模型为

回油泵的动力学模型主要为包括柱塞式回油泵和驱动回油泵的稳控系统电动机，采用理想的液压泵模型，忽略机械损失和制动液泄漏，则回油泵排量如式（2-27）所示。

式中 V_b——回油泵排量；

D_b——柱塞直径；

e——电动机偏心轮偏心距。

泵的输出流量如式（2-28）。

式中 q_b——回油泵输出流量；

S_m——电动机的平均转速。

以上为HCU的动力学模型。以下对制动系统的其他部分进行建模，主要包括制动管路、主缸、轮缸等部分。

制动管路模型包括制动硬管和制动软管，二者都会有由于管壁摩擦所产生的制动液沿程压力损失；对于制动软管，其管壁的弹性变形对压力的影响也要考虑。

制动管路的沿程压力损失动力学模型如式（2-29）。

式中 Δp_g——管路沿程压力损失；

ξ——沿程阻力系数；

L_g——管路长度；

D_g——管路内径；

v——制动液在管路中的平均流速。

由于制动液在制动管路中的流动已经得到了充分的发展，其流动模式为层流，雷诺数λ约为100。则沿程阻力系数ξ在制动硬管中为75/λ，在制动软管中为80/λ。

制动软管属于液容性元件，其管路的体积弹性模量如式（2-30）。

式中 K_g——管路体积模量；

E_g——管路材料弹性模量；

δ——管壁厚度。

综合考虑制动液和软管的体积弹性模量，其等效体积弹性模量K_z如式（2-31）。

由液容性元件的基本方程可得到考虑制动软管弹性变形时的动力学模型，如式（2-32）。

式中 p_g——管路内制动液压力；

V_g——管路内制动液体积；

q_g——制动液流量。

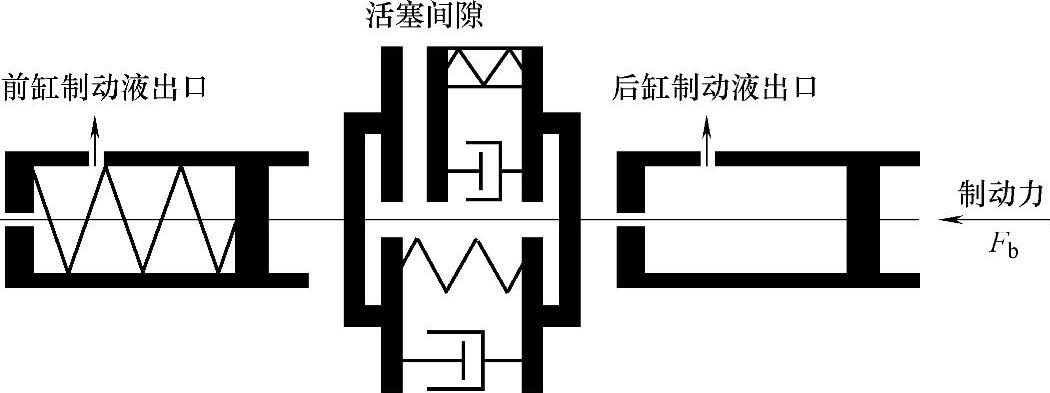
模型依据当前车辆常采用的双腔式主缸建模，考虑了其内部两个活塞的惯性、两活塞间的间隙及弹簧阻尼连接。模型示意图如图2-24所示。

(www.xing528.com)

图2-24 主缸模型

后缸活塞和前缸活塞的运动方程分别如式（2-33）和式（2-34）。

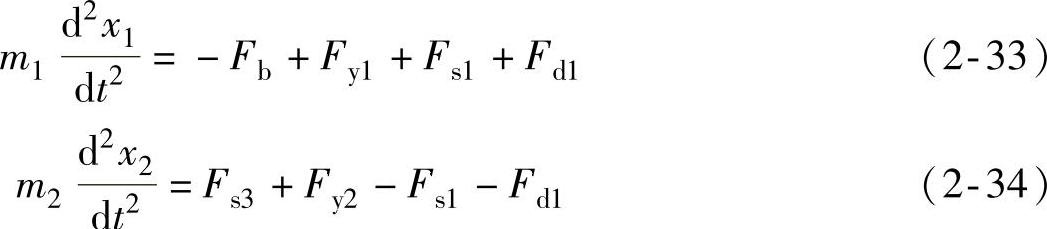
式中 m₁——后缸活塞质量；

m₂——前缸活塞质量；

x₁——后缸活塞位移；

x₂——前缸活塞位移；

F_y1——后缸制动液压力；

F_y2——前缸制动液压力；

F_s1——无间隙连接弹簧力；

F_d1——无间隙连接阻尼力；

F_s3——前缸内弹簧力。

无间隙连接的弹簧力和阻尼力分别如式（2-35）和式（2-36）。

F_s1=（x₁^-x2+G1）k₁ （2-35）

式中 k₁——无间隙连接的弹簧刚度；

f₁——无间隙连接的阻尼系数；

G₁——无间隙连接的弹簧预紧量。后缸和前缸的制动液流量分别如式（2-37）和式（2-38）。

式中 A₁——后缸活塞有效面积；

A₂——前缸活塞有效面积。

在间隙消除之后，主缸的动力学模型与间隙消除之前类似，只是要将有间隙连接的弹簧力和阻尼力再列入模型即可，如式（2-39）和式（2-40）。

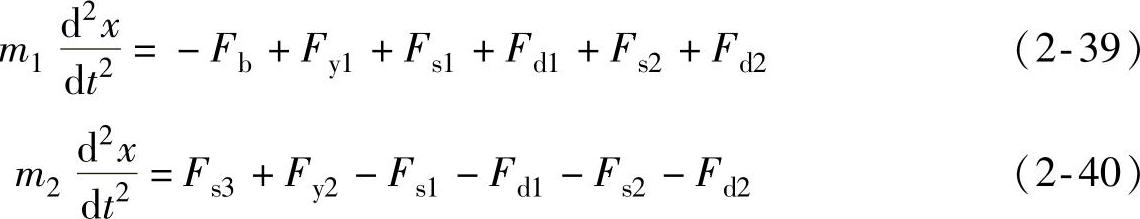
式中 F_s2——有间隙连接的弹簧力；

F_d2——有间隙连接的阻尼力。

F_s2=（x₁-x₂-d）k₂ （2-41）

式中 k₂——有间隙连接的弹簧刚度；

f₂——有间隙连接的阻尼系数；

d——活塞间隙。

制动轮缸模型取盘式制动器，考虑了钳体的惯性、钳体和制动盘之间间隙和接触后的弹簧阻尼等效模型。输入量为制动压力，输出量为制动力，模型如图2-25所示。

制动钳体先要克服回位弹簧的阻力来消除钳体与制动盘之间的间隙，间隙消除后，还要额外克服钳体和制动盘直接接触所产生的等效弹簧阻尼影响，制动钳体运动方程为

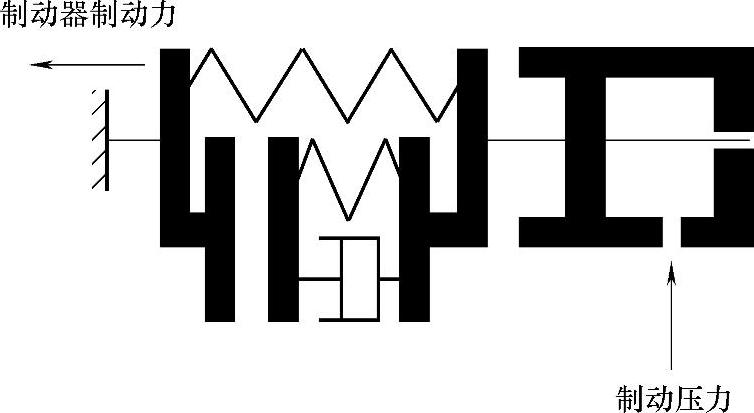
图2-25 轮缸模型

式中 m_q——钳体质量；

x_q——钳体位移；

F_z——制动压力；

F_sq1——弹簧刚度。

回位弹簧力为

式中 k_q1——回位弹簧刚度；

G_q1——回位弹簧预紧量。

间隙消除之后，轮缸的制动力矩为

式中 _μ——制动片摩擦系数；

r_d——制动盘有效摩擦半径。

磁感应强度矢量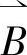在阀体和工作气隙处最强。同样可得到磁场强度的分布，磁场强度在气隙处远远大于其他部分。还得到了线圈外的电流分布情况，该电流是感生电流，其方向与线圈电流相反。麦克斯韦张量法将力计算转化为一个面积分：

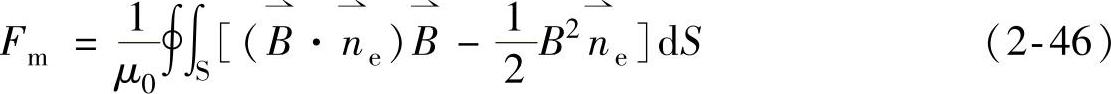
式中 S——气隙中包围器件的任意闭合曲面；

——曲面的单位法向矢量。

此法计算的电磁力在很大程度上取决于有限元网孔的划分密度和闭合曲面的选择，从而限制了计算精度。磁场中贮能增量等于机械能与电能增量的总和，磁场的贮能及伴随贮能计算式分别为

低速运动时用伴随贮能计算磁场力：

计算表明，用以上两种方法计算动铁受力有一定差别。表2-3是阀全开时，用麦克斯韦张量法和能量法（虚功法）计算结果对照。虚功法是更精确的方法，下文电磁力用虚功法计算。

表2-3 麦克斯韦张量法与虚功法计算动铁磁力（单位：N）

阀芯电磁力随气隙减小而增大，对阀芯位置非常敏感（图2-26）。通过插值法，确定电磁力的表达式为

上述电磁阀有限元模型可以研究除材料磁滞效应以外的各种因素对电磁阀性能的影响，包括结构、材料和电流加载方式等。这里仅讨论非工作气隙、材料磁特性等对电磁力的影响。图2-27所示是电磁阀全开状态（左图）和全闭状态（右图），不同非工作气隙的F_m—I曲线族。电磁力随气隙厚度增大而减小，但不如对主工作气隙敏感。这是由于主工作气隙的截面相对较小，更容易形成磁感应强度的“瓶颈”。

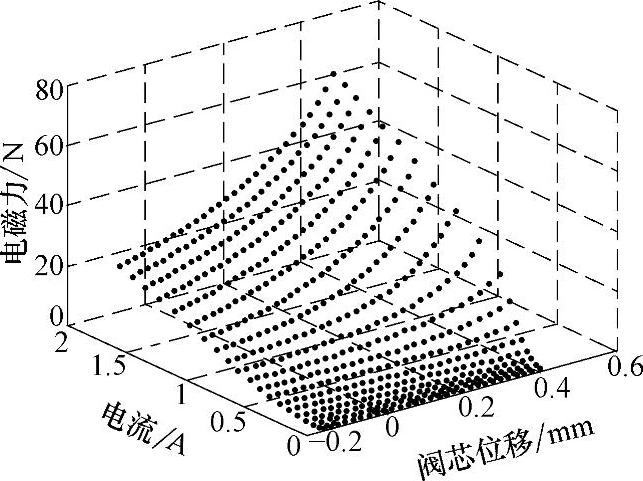
图2-26 动铁电磁力

材料的磁特性，如初始磁导率、最大磁导率、饱和磁感应强度等，对电磁阀性能影响显著。图2-28和图2-29分别显示了两种不同的电磁材料下的电磁力和电感。图中的上下两组曲线分别是阀关闭和开启时的情形。图中实线对应退火处理后的碳素钢16，虚线对应的是碳素钢55。

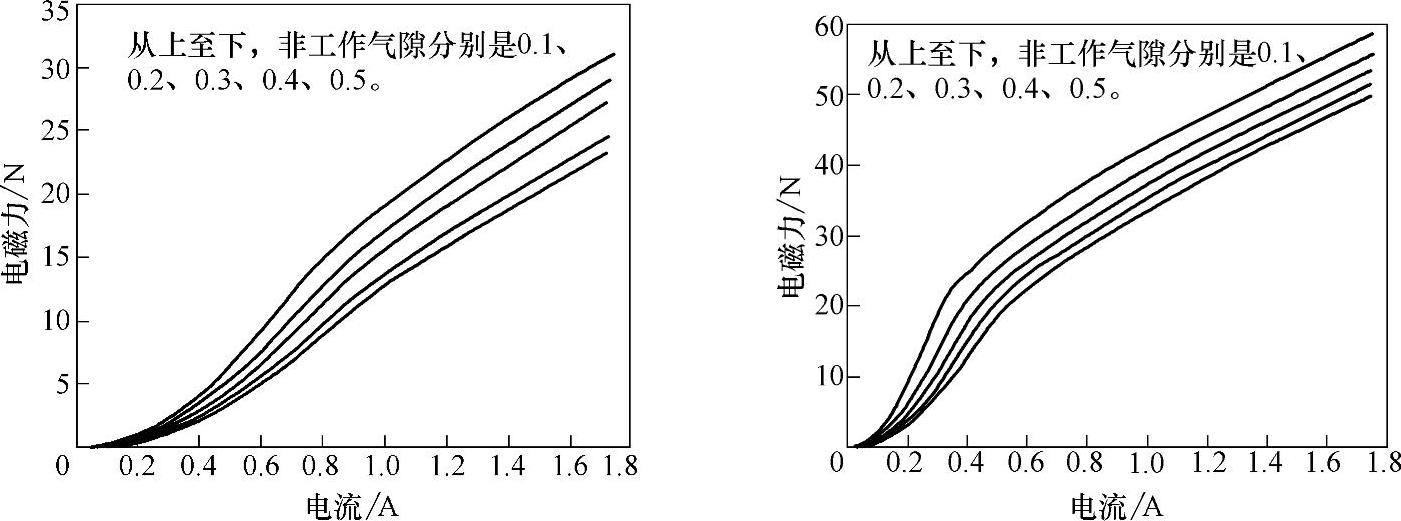
图2-27 非工作气隙对电磁力的影响

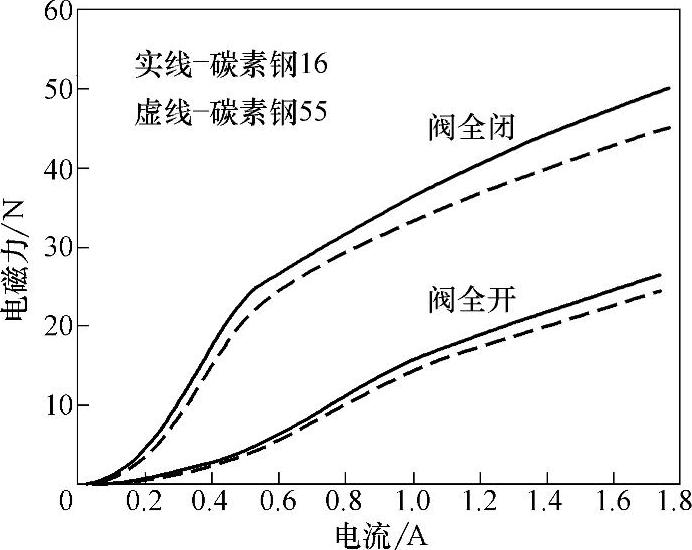
图2-28 磁特性对电磁力的影响

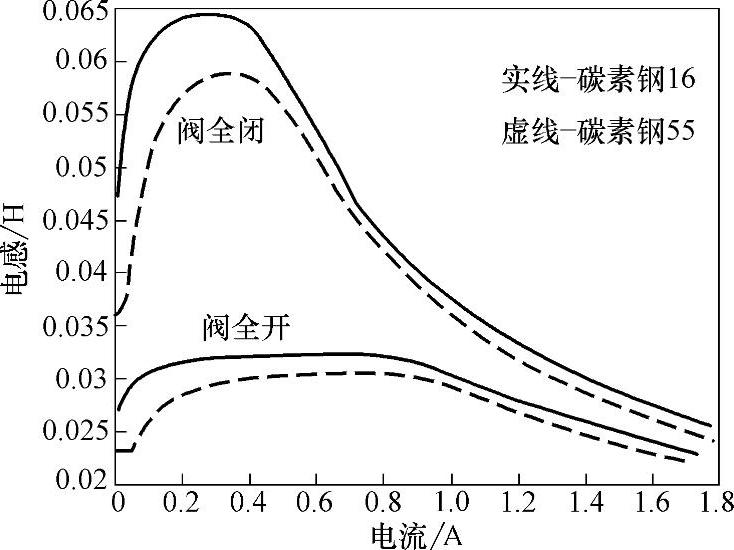
图2-29 磁特性对电感的影响

增压阀和减压阀的节流孔径和阀芯几何形状及位置对稳控系统的压力调节性能有显著影响。本节以增压阀为例，用有限元法建立了流场的牛顿流体层流模型，得到阀口的压力-流量特性，并建立阀芯作用力与阀芯位置和流量的关系。