电磁系统必须具有良好的电磁、流场和机械响应特性。同时，电磁阀要有可靠的防泄漏性能。图2-17所示是电磁阀的结构模型图，图2-18所示为电磁阀工作范围内不同线圈电流和不同阀芯开度状态下，阀芯所受的电磁力。可以看出，电磁力随着阀芯开度的增大（动铁和定铁间距的减小）和电流的增大而增大，并且随着阀芯开度的增大，电磁力相对电流的增长越来越快。
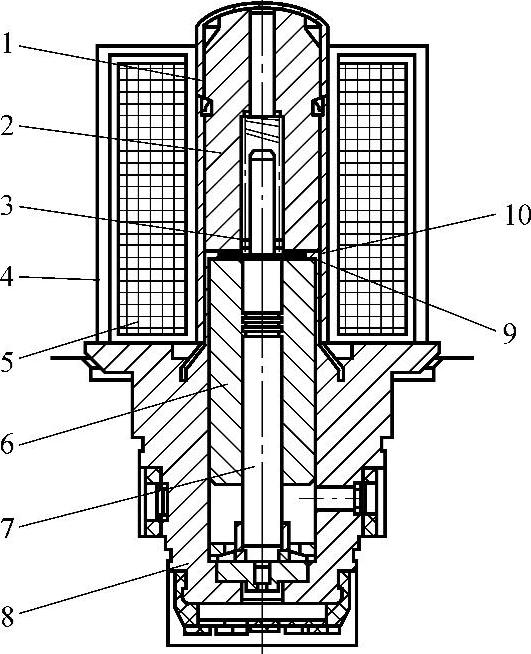
图2-17 电磁阀的结构模型
1—隔磁管 2—定铁 3—回位弹簧 4—线圈扼铁 5—线圈 6—动铁 7—推杆 8—阀体 9—隔磁片 10—工作气隙
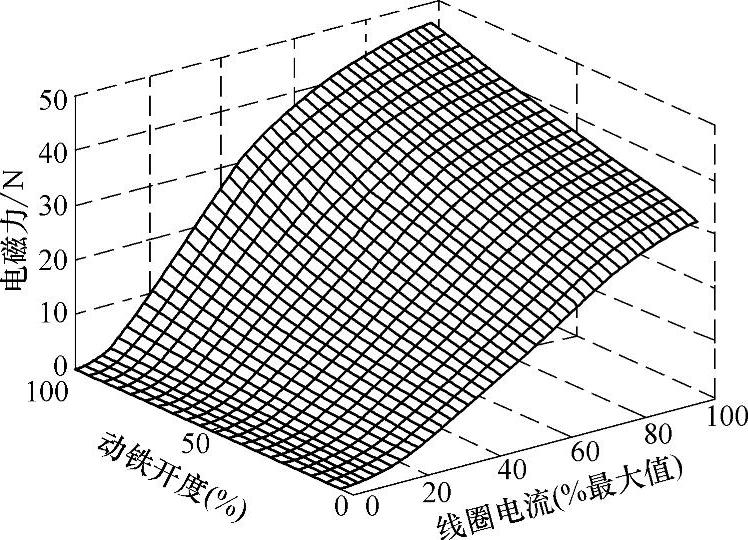
图2-18 电磁力-线圈电流-阀芯开度图
采用轴对称模型，主自由度为矢量磁势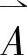
。认为隔磁材料的顶杆与隔磁管具有与空气一致的磁特性，为施加麦克斯韦电磁力标志，假定与动铁直接接触的不是隔磁的顶杆，而是空气。用B-H非线性曲线表征磁性材料的磁特性。磁场建立的时间常数远远小于机械运动的时间常数，因此不考虑阀芯运动与磁场的耦合问题。采用图2-19所示的四边形和三角形平面单元。非工作气隙和工作气隙处磁势降很大，加密其网格。
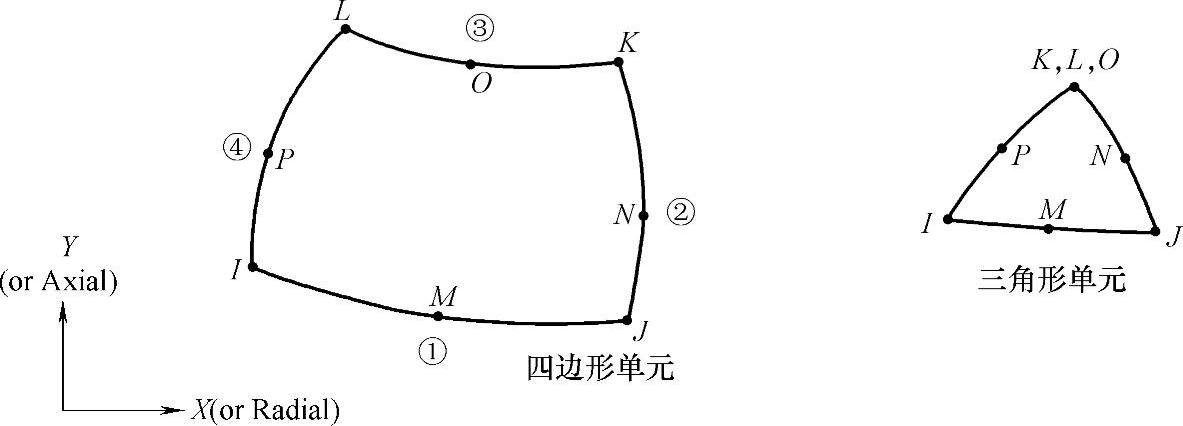
图2-19 单元的形状、结点位置与自由度
电磁场的边界条件可分为三类：狄里克利边界条件（式2-16）、诺依曼边界条件（式2-17）和两者的组合。
(www.xing528.com)
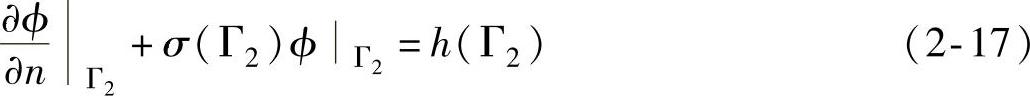
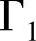和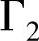
是两类边界；g（
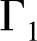），σ（
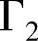），h（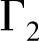
）是位置的一般函数。狄里克利边界条件表示势函数在边界上是定值，而诺依曼边界条件常表达几何和激励源的对称性。磁感应强度在边界上强制地与边界平行。为了处理远场模型时减少单元数目，设立一种特殊的单元类型——远场单元。其实质是一种狄里克利边界条件。图2-20所示包含了轭铁上端部分空气的模型，而图2-21所示为无周边空气模型。尽管轭铁上端的部分空气中确实存在磁场分布，但计算表明这种差别对结果不敏感。为减少计算量，采用的是图2-21所示的模型及边界条件。
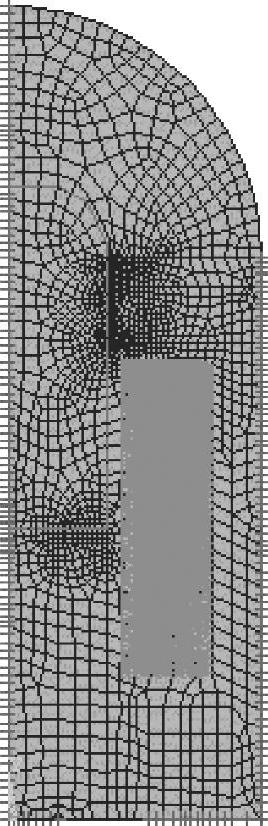
图2-20 含部分周边空气模型
图2-21 无周边空气模型
对于一定的动铁位置x，给电磁线圈加斜坡电压载荷。在前一个载荷步结果的基础上，加以电压载荷增量，重新进行分析。这种方式保存了前一步的涡流密度结果，从而实现涡流损失的时间积分。在求解前耦合线圈电流自由度，后处理程序根据线圈节点上的电流密度求得总电流。每个电压载荷步对应不同的线圈电流，分析整个加载过程，可以建立电磁力Fm和电感L等与线圈电流i的关系。改变动铁的位置x，重复用上述方法进行分析，得到动铁在整个行程中的特性。
磁力线图形象地描述了磁场的分布，阶跃地撤去电压后磁力线分布如图2-22所示。在撤去电压载荷后，导磁体内部的磁场比表面衰减得慢。磁场在导磁体的表面与内部不同快慢的变化率与导体内感生电流有关。图2-22显示，动铁中心磁力线很少。如果钻去动铁中部的部分材料，在不影响磁场下减少动铁质量，从而缩短电磁阀响应时间，减小阀芯落座冲击。
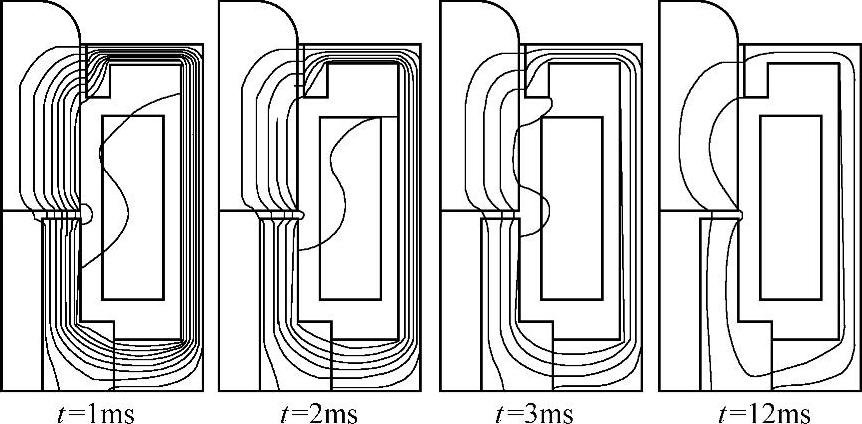
图2-22 磁力线分布图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
