稳控系统仿真平台模型及技术要点

车辆作为典型的机电系统，其模型是研究该系统的有效工具。为了对车辆稳控系统进行分析，搭建稳控系统仿真平台可为控制算法评价、调试、标定匹配和性能分析等提供良好的环境。稳控系统仿真平台是稳控系统控制方法和算法的基础，仿真平台由驾驶人模型、车辆动力学模型、轮胎模型、路面模型、制动系统模型、ECU模型和HCU模型等组成。图2-7所示为稳控系统仿真平台示意图。

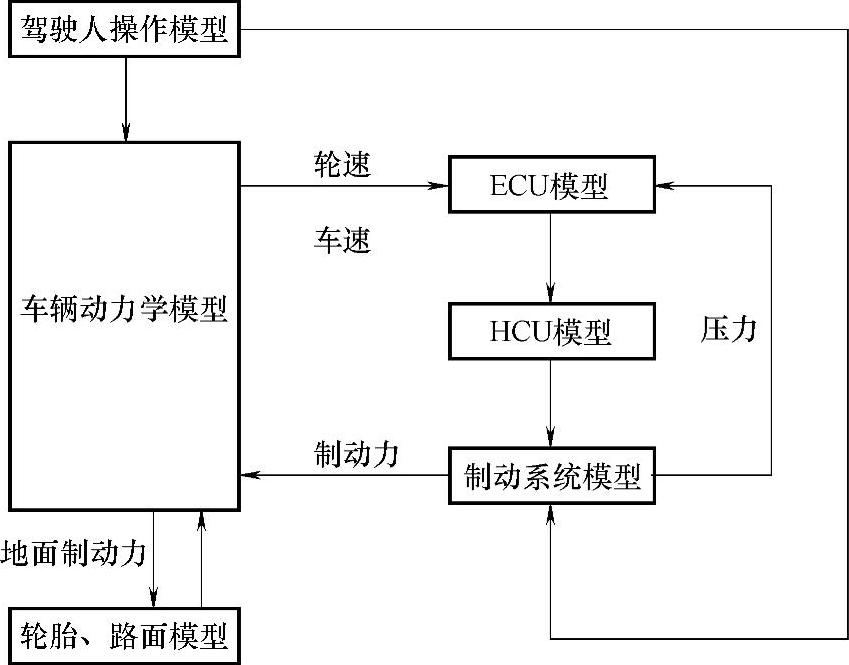
图2-7 稳控系统仿真平台模型

在仿真平台中，驾驶人操作模型优先级最高，车辆的运行状态响应驾驶人的操作意图，根据驾驶人操作可以仿真不同的稳控系统制动工况。车辆的运动依赖于轮胎所受的力，如纵向力和侧向力等，轮胎、路面模型是车辆运动的基础，稳控系统仿真中的各种路面附着工况，如高附着路面制动、低附着路面制动、对接路面制动以及对开路面制动等，就是依靠轮胎、路面模型的合理设计来完成的。车辆动力学模型是研究稳控系统的载体，车辆动力学模型根据驾驶人操作、稳控系统控制的制动压力、地面的纵向力/侧向力等计算车辆的状态，如车身状态、车轮状态等。ECU模型可以用不同的控制方法来实现，如逻辑门限值方法、PID控制方法、模糊控制方法等，从而可以对控制方法和控制算法进行研究；在HCU模型和制动系统模型上可以进行制动压力动态特性的分析。以上各部分模型各自独立又相互关联，组合在一起构成了稳控系统仿真平台。为适用不同的稳控系统仿真目的，本章分别建立了2自由度和7自由度车辆动力学模型，如图2-8、图2-9所示。车辆动力学模型是典型的连续时间系统，可以用微分方程来描述。2自由度车辆动力学模型也称为1/4车辆制动模型或单轮模型，共有2个自由度，即沿X方向的平动和车轮的转动。

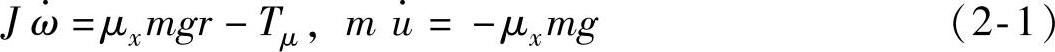
式中 m——车辆质量；

J——车轮转动惯量；

ω——车轮加速度；

μ_x——地面附着系数；

r——车轮半径；

T_μ——制动力矩；

u——车速。

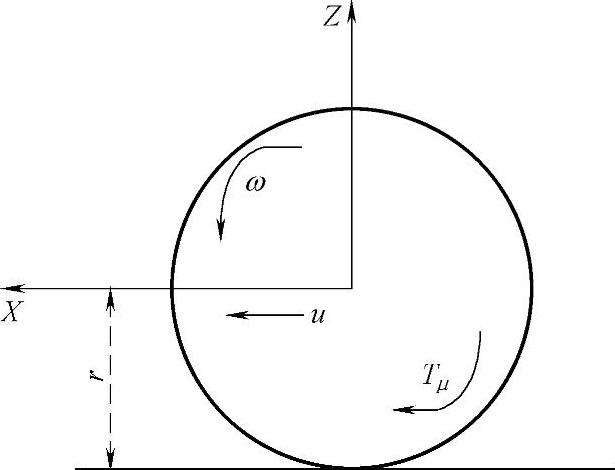
图2-8 2自由度汽车模型

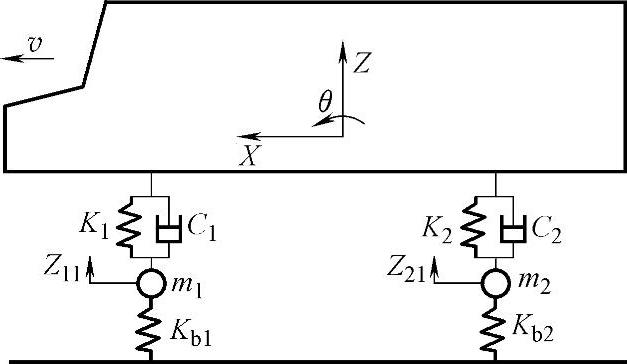
图2-9 7自由度汽车模型

1/4车辆制动模型只考虑了车辆的平动和车轮的转动，是研究稳控系统最简单的模型，它可以反映最基本的受力、运动和滑移率的关系，可以对控制方法进行原理的分析和设计。

采用2自由度车辆模型，考虑到大侧向加速度时的非线性，系统状态参量及观测量为

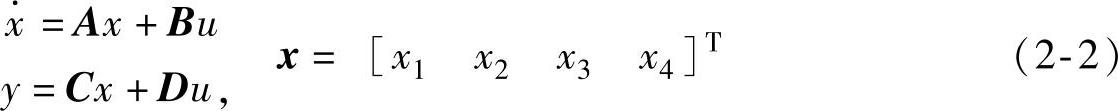
式中，x为系统状态参量，u为输入量，y为观测量，A为状态矩阵，B为控制矩阵，C为输出矩阵，D为传递矩阵。

7自由度车辆动力学模型，也可称为1/2车辆制动力模型或双轮模型。其包括7个自由度：整车的前进方向运动自由度X，垂直运动自由度Z和俯仰运动自由度θ；前轮垂直运动自由度Z₁₁和旋转运动自由度ω₁₁；后轮垂直运动自由度Z₂₁和旋转运动自由度ω₂₁。

运动方程为

整车前进方向运动方程

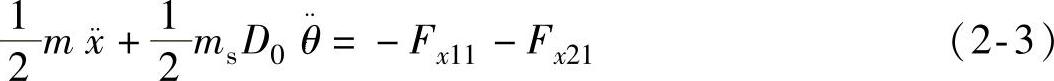(www.xing528.com)

车身垂直方向运动方程

车身俯仰运动方程

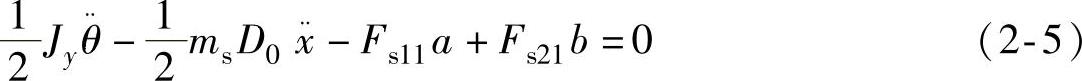
前轮垂直运动方程

后轮垂直运动方程

前轮旋转运动方程

后轮旋转运动方程

轮胎的纵向力

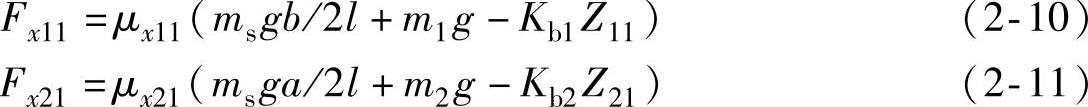
悬架所受的力

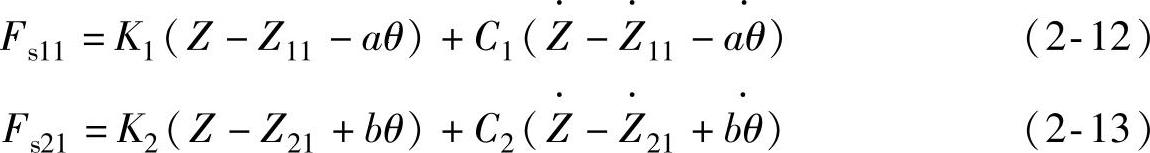
7自由度的1/2车辆制动模型可用于直线制动过程中稳控系统的控制仿真，它考虑了汽车制动过程中的载荷在前后轮上的转移，比单轮模型更加符合实际工况。相关参数说明见表2-1。

表2-17 自由度车辆动力学模型参数说明

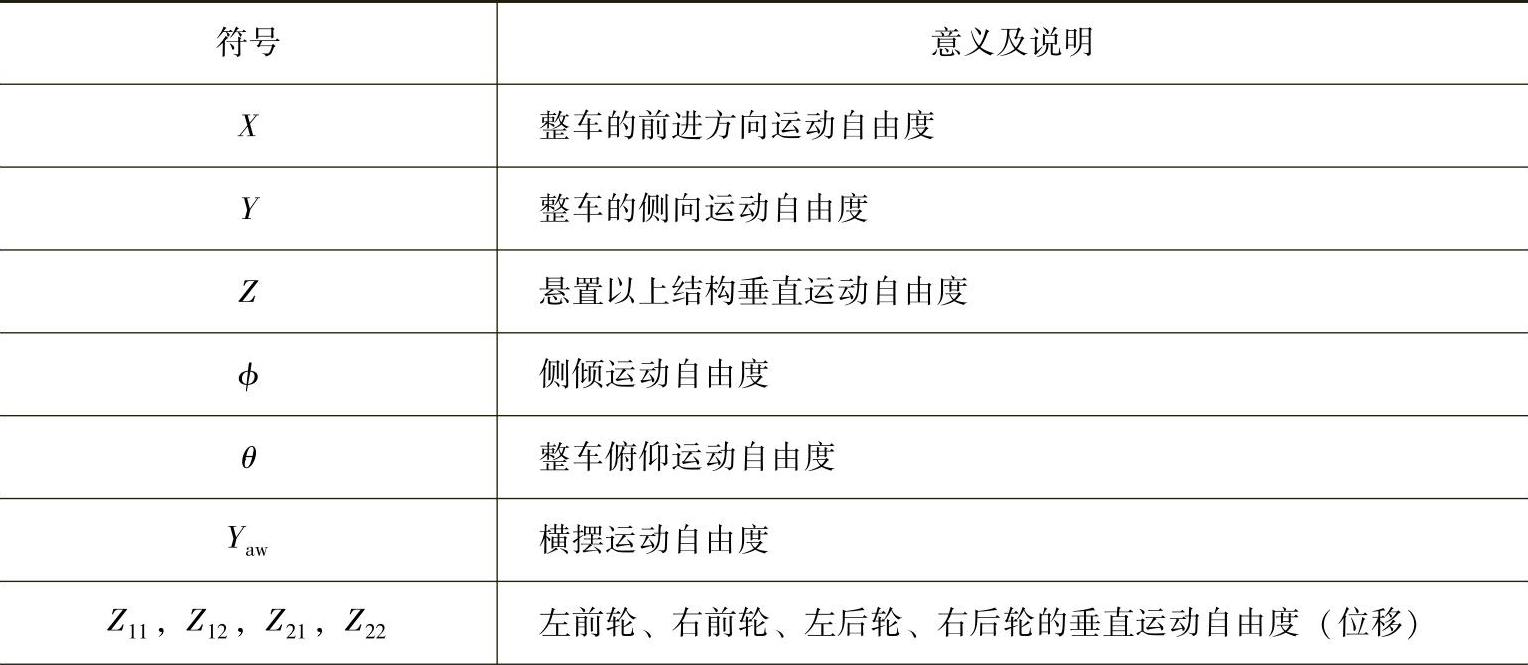
（续）

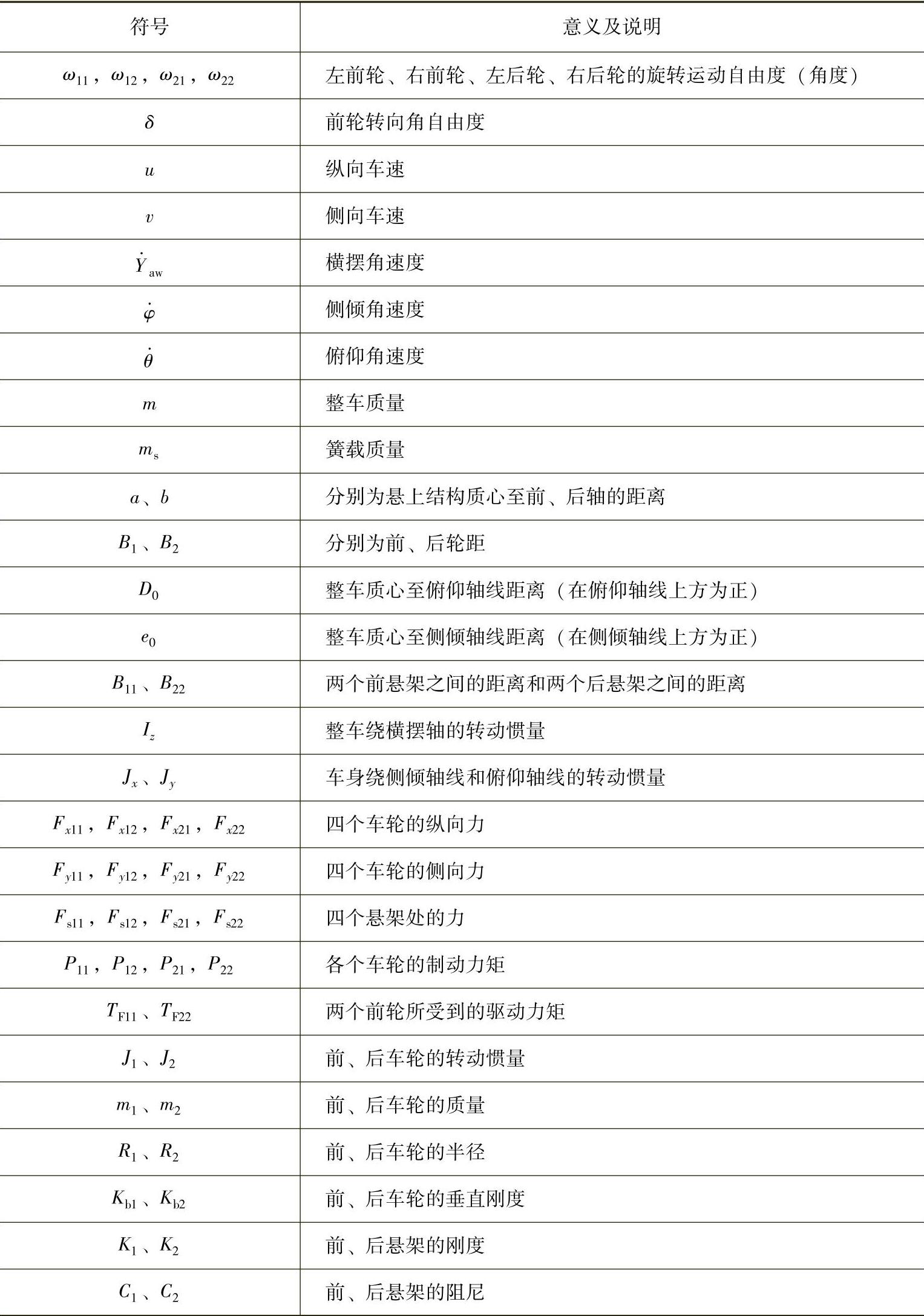
轮胎纵侧向力F_x11，F_x12，F_x21，F_x22、Fy11，Fy12，Fy21，Fy22，需要利用轮胎模型进行计算，转向角自由度的方程需要根据实际仿真情况给出，如阶跃输入、正弦输入或实车测试值输入等。