GNSS测量技术：坐标系统转换简介

1. 空间直角坐标与大地坐标间的转换

将同一坐标参照系下大地坐标(B，L，H，)转换为空间直角坐标系(X，Y，Z)的公式为:

图2.2 WGS-84坐标系

式中: N为卯酉圈的半径; a为参考椭球的长半轴; b为参考椭球的短半轴; e为参考椭球的第一偏心率; f为参考椭球的扁率并且

将同一坐标系参照下的空间直角坐标系( X，Y，Z) 转换为大地坐标(B，L，H)的公式为:

需要指出的是，在采用式(2.5)进行空间直角坐标到大地坐标的转换过程中，由于计算大地纬度B时，需要用到大地高H，而计算大地高H时，又需要用到大地纬度B，因此，无法直接由空间直角坐标，而须采用迭代计算的方法。具体计算时，可先使用(2.6)求出B的初值:

然后，利用该初值使用式(2.5)和式(2.4)来求出H、N的值，再利用所求出的H和N的初值使用式(2.5)再次求定B值。如此反复，直至所求定的B、H、N收敛为止。

也可采用如下直接算法将空间直角坐标转换为空间大地坐标:

式中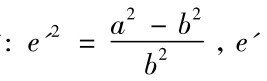为参考椭球的第二偏心率;(www.xing528.com)

2. 不同空间直角坐标间的转换

当两个空间直角坐标系的坐标换算既有旋转又有平移时，则存在三个平移参数和三个旋转参数，再顾及两个坐标系尺度不尽一致，从而还有一个尺度变化参数(见图2.3)，共计有七个参数相应的坐标变换公式为:

式中ΔX0，ΔY0，ΔZ0三个平移参数; εX，εY，εZ为三个旋转参数，m为尺度变化参数，上式为两个不同空间直角坐标之间的转换模型(布尔莎模型)，其中含有7个转换参数，为了求得7个转换参数，至少需要3个公共点，当多于3个公共点时，可按最小二乘法求得7个参数的最或是值。

图2.3 转换参数

3. 坐标与地方坐标系之间的转换

GNSS所获得的坐标是WGS-84坐标系的大地坐标，而我们常用的坐标系统为54系、80系和地方坐标系，因此需要将WGS-84坐标系的大地坐标转换为我们常用的平面直角坐标。其转换步骤如图2.4所示。当测区不大时，可以采用三参数法(认为三个旋转角为0，尺度变化为0)，当测区较大或要求精度高时采用7参数法即布尔莎模型。

图2.4 转换流程图