钢混凝土组合梁|钢结构工程常用图表手册

1）在进行组合梁截面承载能力验算时，跨中及中间支座处混凝土翼板的有效宽度b_e（图2-56）应按下式计算：

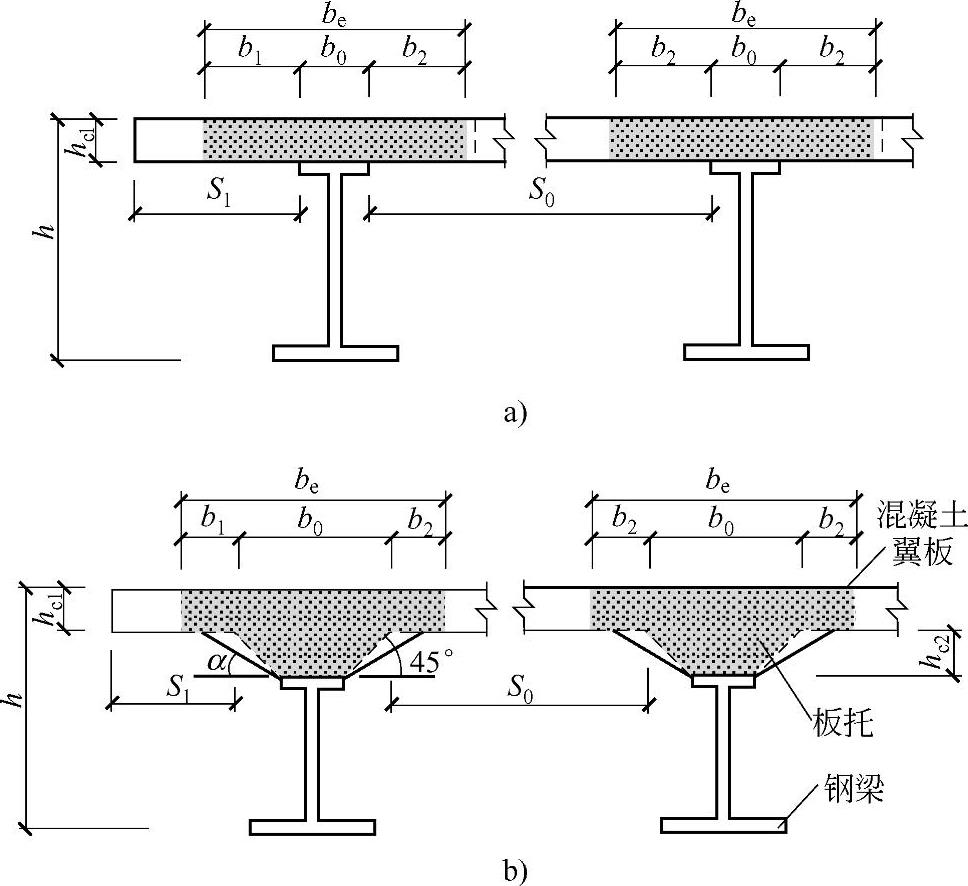
图2-56 混凝土翼板的计算宽度

a）不设板托的组合梁 b）设板托的组合梁

b_e=b₀+b₁+b₂ （2-148）

式中 b₀——板托顶部的宽度：当板托倾角α<45°时，应按α=45°计算；当无板托时，则取钢梁上翼缘的宽度；当混凝土板和钢梁不直接接触（如之间有压型钢板分隔）时，取栓钉的横向间距，仅有一列栓钉时取0；

b₁、b₂——梁外侧和内侧的翼板计算宽度，各取梁等效跨径l_e的1/8。此外，b₁不应超过翼板实际外伸宽度S₁；b2不应超过相邻钢梁上翼缘或板托间净跨S₀的1/2；

l_e——等效跨径。对于简支组合梁，取为简支组合梁的跨度l。对于连续组合梁，中间跨正弯矩区取为0.6l，边跨正弯矩区取为0.8l，支座负弯矩区取为相邻两跨跨度之和的0.2倍。

2）完全抗剪连接组合梁的抗弯强度应按下列规定计算：

① 正弯矩作用区段

a.塑性中和轴在混凝土翼板内（图2-57），即Af≤b_eh_c1f_c时：

M≤b_exf_cy （2-149）

式中 M——正弯矩设计值；

x——混凝土翼板受压区高度，按式（2-150）计算：

x=Af/（b_ef_c） （2-150）

A——钢梁的截面面积；

y——钢梁截面应力的合力至混凝土受压区截面应力的合力间的距离；

f_c——混凝土抗压强度设计值。

b.塑性中和轴在钢梁截面内（图2-58），即Af>b_eh_c1f_c时：

M≤b_eh_c1f_cy₁+A_cfy₂ （2-151）

式中 A_c——钢梁受压区截面面积，按式（2-152）计算：

A_c=0.5（A-b_eh_c1f_c/f） （2-152）

y₁——钢梁受拉区截面形心至混凝土翼板受压区截面形心的距离；

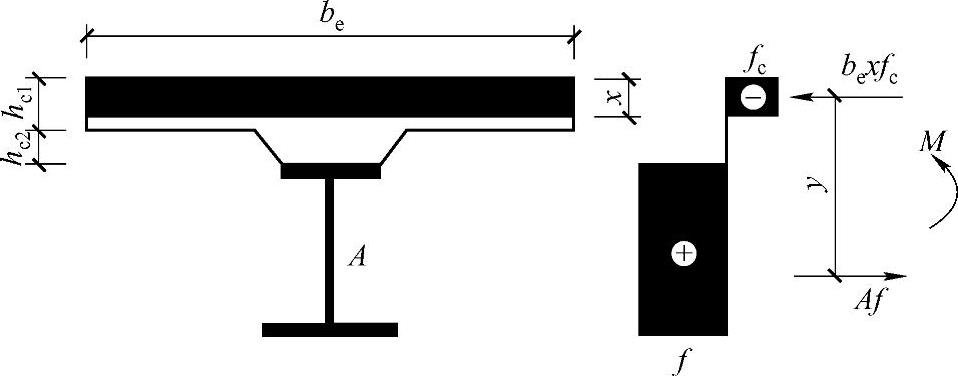
图2-57 塑性中和轴在混凝土翼板内时的组合梁截面及应力图形

y₂——钢梁受拉区截面形心至钢梁受压区截面形心的距离。

② 负弯矩作用区段（图2-59）

M′≤M_s+A_stf_st（y₃+y₄/2）

（2-153）

M_s=（S₁+S₂）f （2-154）

式中 M′——负弯矩设计值；

S₁、S₂——钢梁塑性中和轴（平分钢梁截面积的轴线）以上和以下截面对该轴的面积矩；

图2-58 塑性中和轴在钢梁内时的组合梁截面及应力图形

A_st——负弯矩混凝土翼板有效宽度范围内的纵向钢筋截面面积；

f_st——钢筋抗拉强度设计值；

y₃——纵向钢筋截面形心至组合梁塑性中和轴的距离，根据截面轴力平衡式（2-155）求出钢梁受压区面积A_c，取钢梁拉压区交界处位置为组合梁塑性中和轴位置：

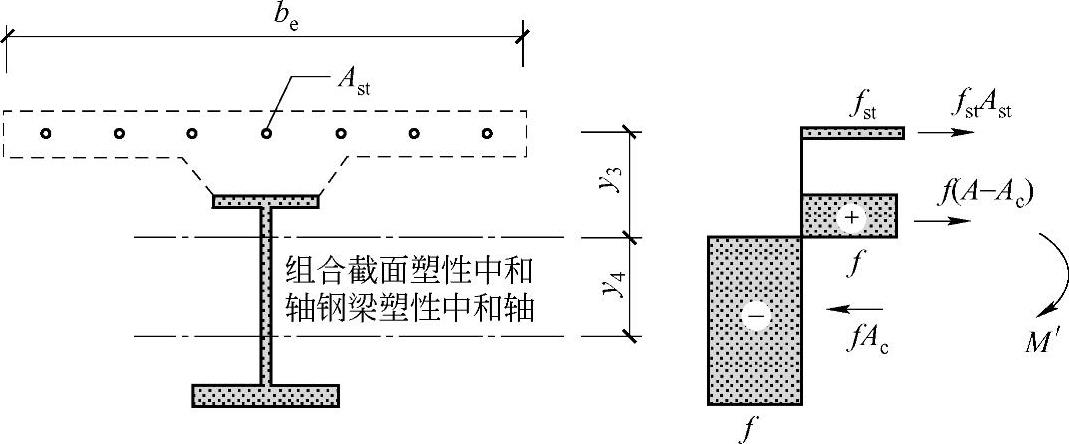
图2-59 负弯矩作用时组合梁截面及应力图形

f_stA_st+f（A-A_c）=fA_c （2-155）

y₄——组合梁塑性中和轴至钢梁塑性中和轴的距离。当组合梁塑性中和轴在钢梁腹板内时，取y₄=A_stf_st/（2t_wf），当该中和轴在钢梁翼缘内时，可取y₄等于钢梁塑性中和轴至腹板上边缘的距离。

3）部分抗剪连接组合梁在正弯矩区段的抗弯强度宜按下列公式计算（图2-60）：

x=n_rN_v^c/（b_ef_e） （2-156）

M_u，r=nrN^c_vy₁+0.5（Af-n_rN^c_v）y₂ （2-157）

式中 M_u，r——部分抗剪连接时组合梁截面正弯矩抗弯承载力；

n_r——部分抗剪连接时最大正弯矩验算截面到最近零弯矩点之间的抗剪连接件数目；

N^c_v——每个抗剪连接件的纵向抗剪承载力，按4）的有关公式计算。

y₁、y₂——如图2-60所示，可按公式（2-158）所示的轴力平衡关系式确定受压钢梁的面积A_c，进而确定组合梁塑性中和轴的位置：

图2-60 部分抗剪连接组合梁计算简图

A_c=（Af-n_rN^c_v）/（2f） （2-158）

计算部分抗剪连接组合梁在负弯矩作用区段的抗弯强度时，仍按公式（2-153）计算，但A_stf_st应取n_rN^c_v和A_stf_st两者中的较小值，n_r取为最大负弯矩验算截面到最近零弯矩点之间的抗剪连接件数目。

4）组合梁的抗剪连接件宜采用圆柱头焊钉，也可采用槽钢或有可靠依据的其他类型连接件（图2-61）。单个抗剪连接件的抗剪承载力设计值由下列公式确定：

图2-61 连接件的外形(www.xing528.com)

a）圆柱头焊钉连接件 b）槽钢连接件

① 圆柱头焊钉连接件

式中 E_c——混凝土的弹性模量；

A_s——圆柱头焊钉钉杆截面面积；

f_u——圆柱头焊钉极限抗拉强度设计值，需满足《电弧螺柱焊用圆柱头焊钉》（GB/T 10433—2002）的要求。

② 槽钢连接件

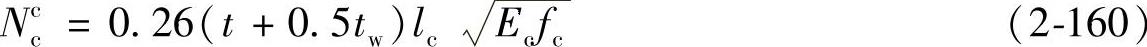
式中 t——槽钢翼缘的平均厚度；

t_w——槽钢腹板的厚度；

l_c——槽钢的长度。

槽钢连接件通过肢尖肢背两条通长角焊缝与钢梁连接，角焊缝按承受该连接件的抗剪承载力设计值N_v^c进行计算。

5）对于用压型钢板混凝土组合板作翼板的组合梁（图2-62），其焊钉连接件的抗剪承载力设计值应分别按以下两种情况予以降低：

图2-62 用压型钢板作混凝土翼板底模的组合梁

a）肋与钢梁平行的组合梁截面 b）肋与钢梁垂直的组合梁截面 c）压型钢板作底模的楼板剖面

① 当压型钢板肋平行于钢梁布置（图2-62a），b_w/h_e<1.5时，按公式（2-159）算得的N^c_v应乘以折减系数β_v后取用。β_v值按下式计算：

式中 b_w——混凝土凸肋的平均宽度，当肋的上部宽度小于下部宽度时（图2-62c），改取上部宽度；

h_e——混凝土凸肋高度；

h_d——焊钉高度。

② 当压型钢板肋垂直于钢梁布置时（图2-62b），焊钉连接件承载力设计值的折减系数按下式计算：

式中 n₀——在梁某截面处一个肋中布置的焊钉数，当多于3个时，按3个计算。

6）当采用柔性抗剪连接件时，抗剪连接件的计算应以弯矩绝对值最大点及支座为界限，划分为若干个区段（图2-63），逐段进行布置。每个剪跨区段内钢梁与混凝土上翼板交界面的纵向剪力V_s按下列公式确定：

图2-63 连续梁剪跨区划分图

① 正弯矩最大点到边支座区段，即m₁区段，V_s取Af和b_eh_c1f_c中的较小者。

② 正弯矩最大点到中支座（负弯矩最大点）区段，即m₂和m₃区段：

V_s=min{Af，b_eh_c1f_c}+A_stf_st （2-163）

按照完全抗剪连接设计时，每个剪跨区段内需要的连接件总数n_f，按下式计算：

n_f=V_s/N_f^c （2-164）

部分抗剪连接组合梁，其连接件的实配个数不得少于n_f的50%。

按公式（2-164）算得的连接件数量，可在对应的剪跨区段内均匀布置。当在此剪跨区段内有较大集中荷载作用时，应将连接件个数n_f按剪力图面积比例分配后再各自均匀布置。

7）组合梁板托及翼缘板纵向抗剪承载力验算时，应分别验算图2-64所示的纵向受剪界面a-a、b-b、c-c及d-d。

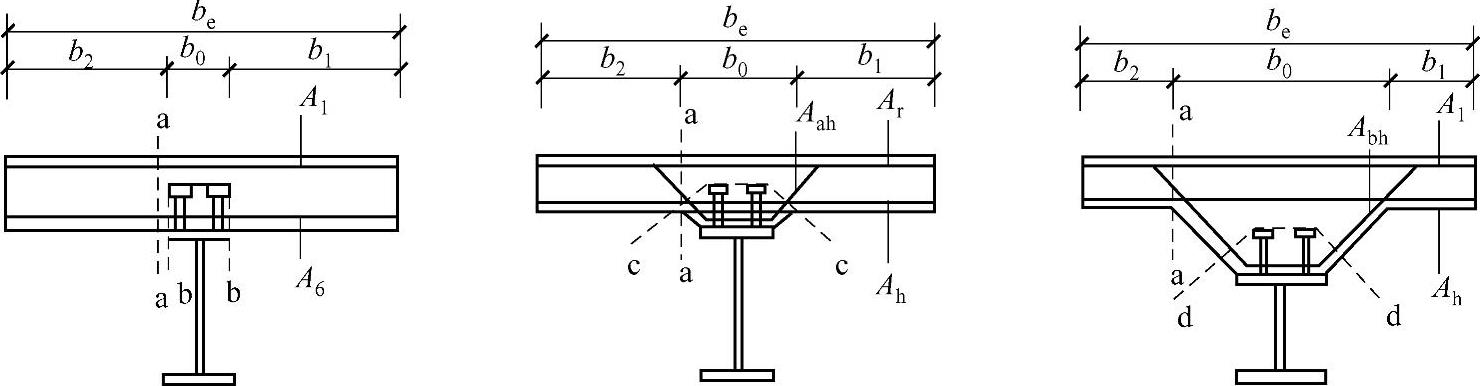
图2-64 混凝土板纵向受剪界面

图中 A₁——混凝土板顶部附近单位长度内钢筋面积的总和（mm²/mm），包括混凝土板内抗弯和构造钢筋；

A_h、A_bh——分别为混凝土板底部、承托底部单位长度内钢筋面积的总和（mm²/mm）。

8）组合梁承托及翼缘板界面纵向受剪承载力计算应符合下列规定：

v_l，1≤v_lu，1 （2-165）

式中 v_lu，1——单位纵向长度内界面抗剪承载力（N/mm），取式（2-166）和式（2-167）的较小值：

v_lu，1=0.7f_tb_f+0.8A_ef_r （2-166）

v_lu，1=0.25b_ff_c （2-167）

f_t——混凝土抗拉强度设计值（N/mm²）；

b_f——受剪界面的横向长度，按图2-64中所示的a-a、b-b、c-c及d-d连线在抗剪连接件以外的最短长度取值（mm）；

A_e——单位长度上横向钢筋的截面面积（mm²/mm），按图2-64和表2-40取值；

f_r——横向钢筋的强度设计值（N/mm²）。

表2-40 单位长度上横向钢筋的截面面积Ae

9）组合梁边梁混凝土翼板的构造应满足图2-65的要求。有托板时，伸出长度不宜小于h_c2；无板托时，应同时满足伸出钢梁中心线不小于150mm、伸出钢梁翼缘边不小于50mm的要求。

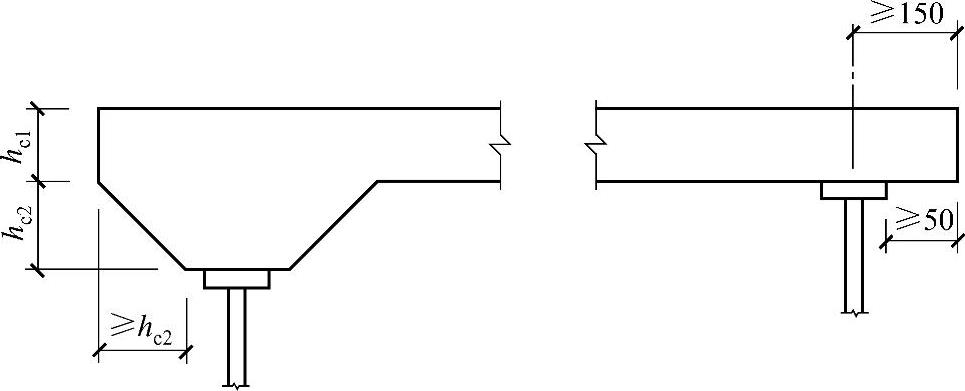
图2-65 边梁构造图