1)弯矩作用在两个主平面内的拉弯构件和压弯构件(圆管截面除外),其截面强度应按下列规定计算:

弯矩作用在两个主平面内的圆形截面拉弯构件和压弯构件,其截面强度应按下列规定计算:

式中 γx、γy——与截面模量相应的截面塑性发展系数,应按表2-25采用;
γm——对于实腹圆形截面取1.2,圆管截面取1.15;
An——圆管净截面面积;
Wn——圆管净截面模量。
表2-25 截面塑性发展系数γx、γy值
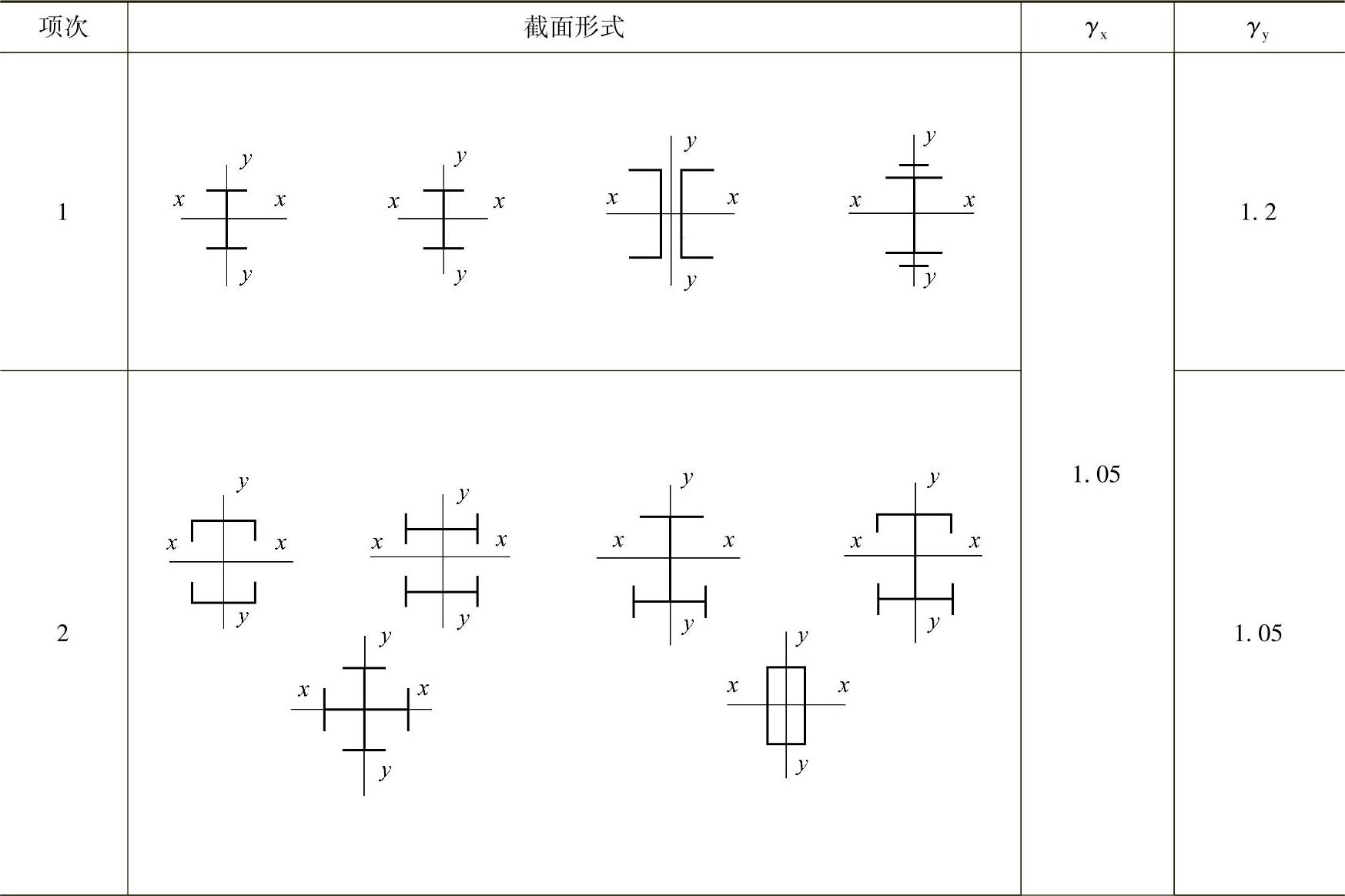
(续)
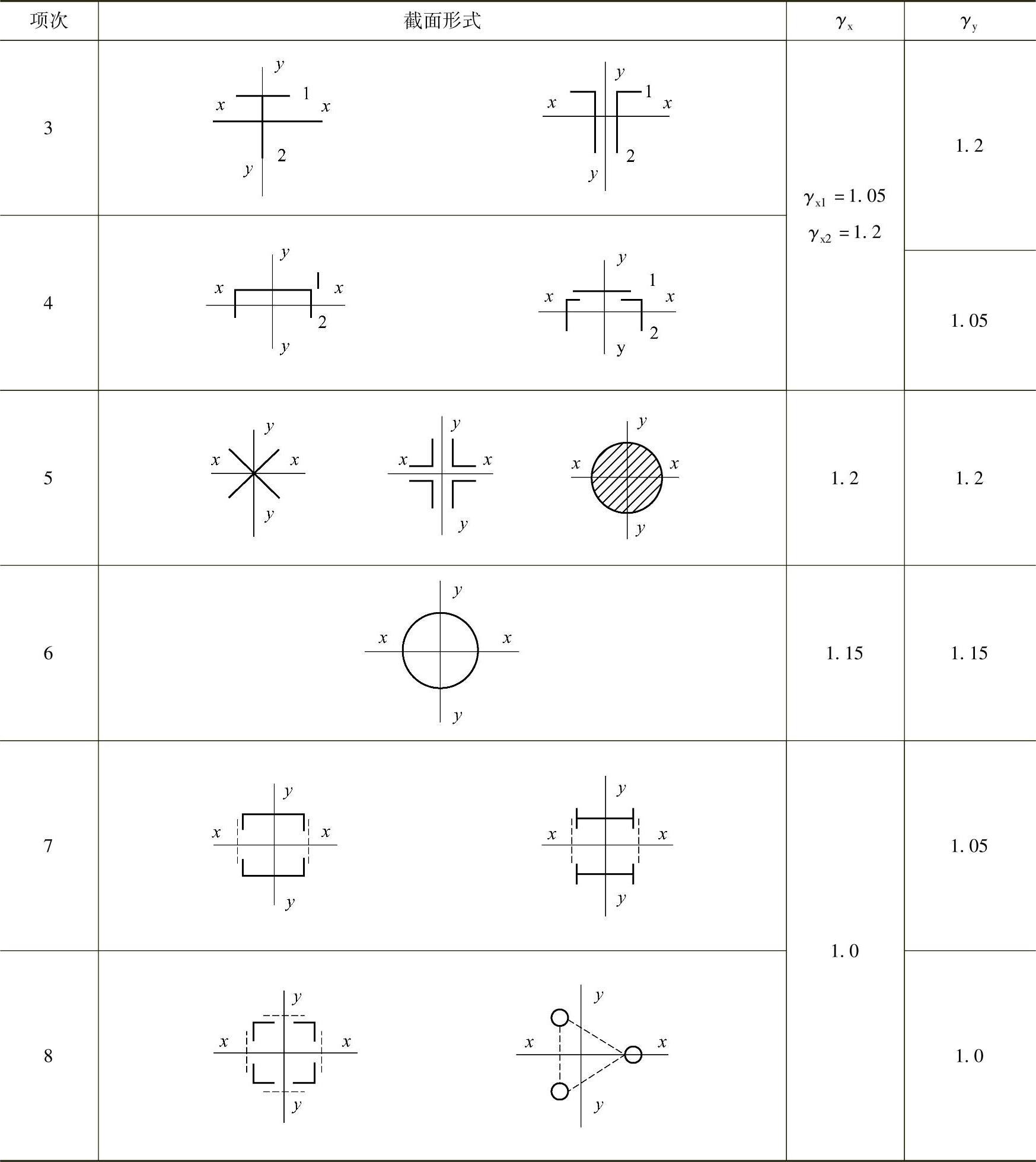
当压弯构件受压翼缘的自由外伸宽度与其厚度之比大于13εk而不超过15εk时应取γx=1.0。
需要验算疲劳强度的拉弯、压弯构件,宜取γx=γy=γm=1.0
2)弯矩作用在两个主平面内的双肢格构式压弯构件,其稳定性应按下列规定计算:
① 按整体计算:
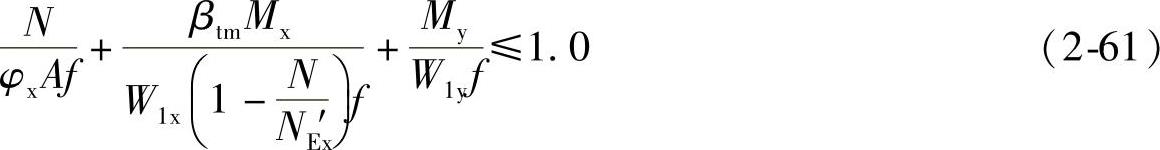
式中 W1y——在My作用下,对较大受压纤维的毛截面模量。
② 按分肢计算:
在N和Mx作用下,将分肢作为桁架弦杆计算其轴心力,My按公式(2-62)和公式(2-63)分配给两分肢(图2-13),然后按《钢结构设计规范》2013年征求意见稿)第8.2.1条的规定计算分肢稳定性。
分肢1:
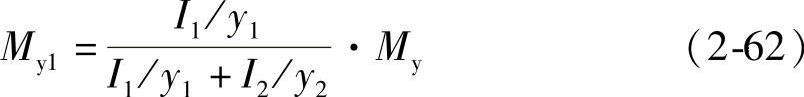
分肢2:

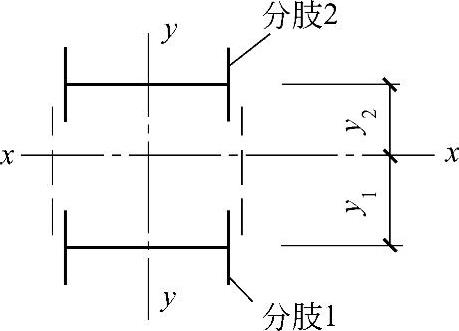
图2-13 格构式构件截面
式中 I1、I2——分肢1、分肢2对y轴的惯性矩;
y1、y2——My作用的主轴平面至分肢1、分肢2轴线的距离。
3)单层厂房框架下端刚性固定的带牛腿等截面柱在框架平面内的计算长度应按下列公式确定:

式中 h1、h——分别为柱在牛腿表面以下的高度和柱总高度(图2-14);
R——与柱连接的斜梁线刚度之和与柱线刚度之比,按式(2-65)计算:

αR——和比值R有关的系数,应按下列方法计算:
当R<0.2时
αR=1.5-2.5R (2-66)
当R≥0.2时
αR=1.0 (2-67)
αN——考虑压力变化的系数,应按下列方法计算:
当γ>0.2时
αN=1.0 (2-68)
当γ≤0.2时

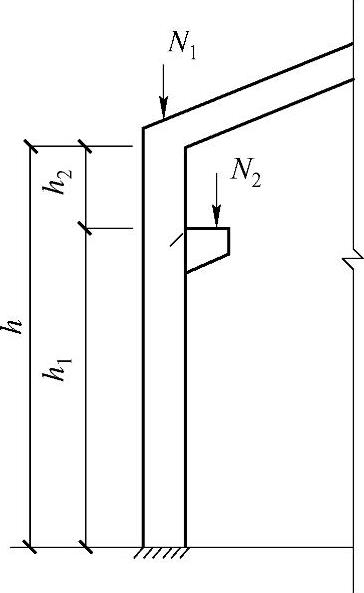
图2-14 单层厂房框架示意
γ——柱上下段压力比。
4)单层厂房框架下端刚性固定的阶形柱,在框架平面内的计算长度应按下列规定确定:
① 单阶柱
a.下段柱的计算长度系数μ2:当柱上端与横梁铰接时,应按表2-26的数值乘以表2-27的折减系数;当柱上端与横梁刚接时,应按表2-28的数值乘以表2-27的折减系数。
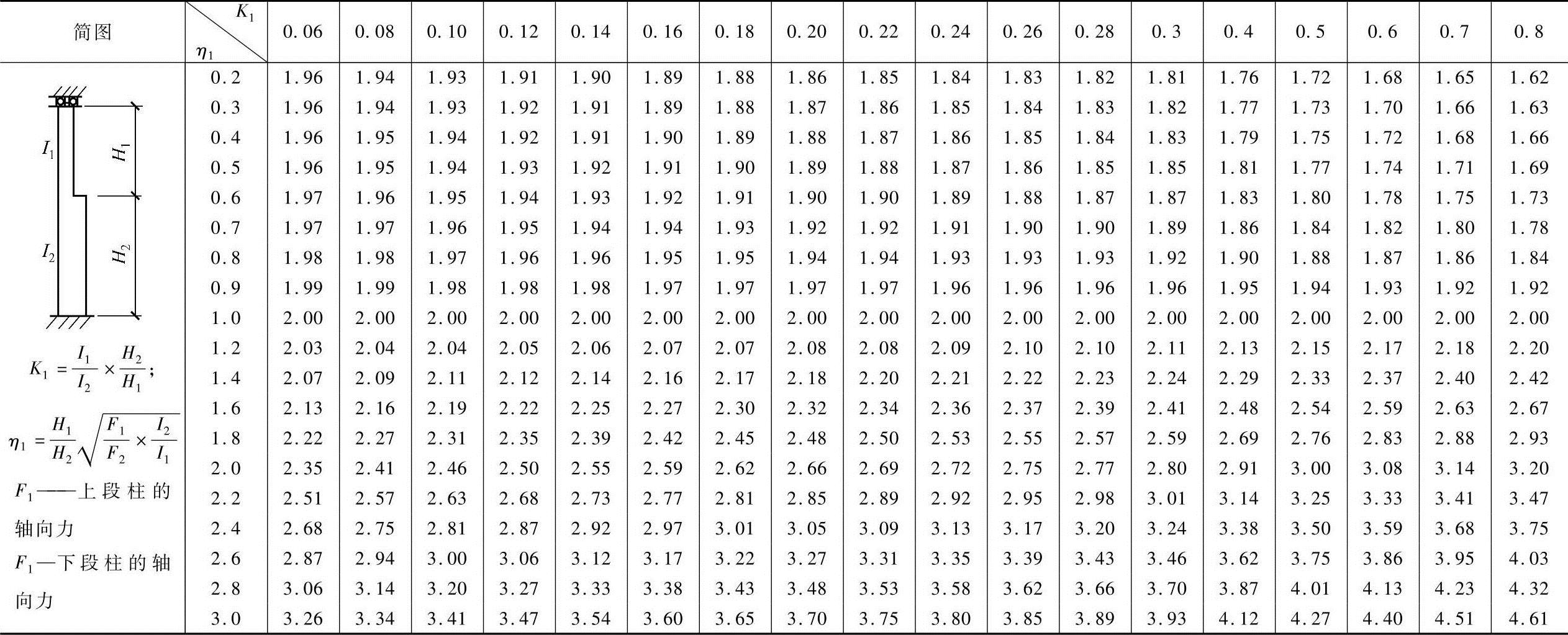
表2-26 柱上端为自由的单阶柱下段的计算长度系数μ2
注:表中的计算长度系数μ值按下式计算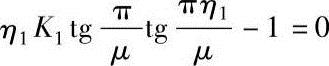
表2-27 单层厂房阶形柱计算长度的折减系数(https://www.xing528.com)

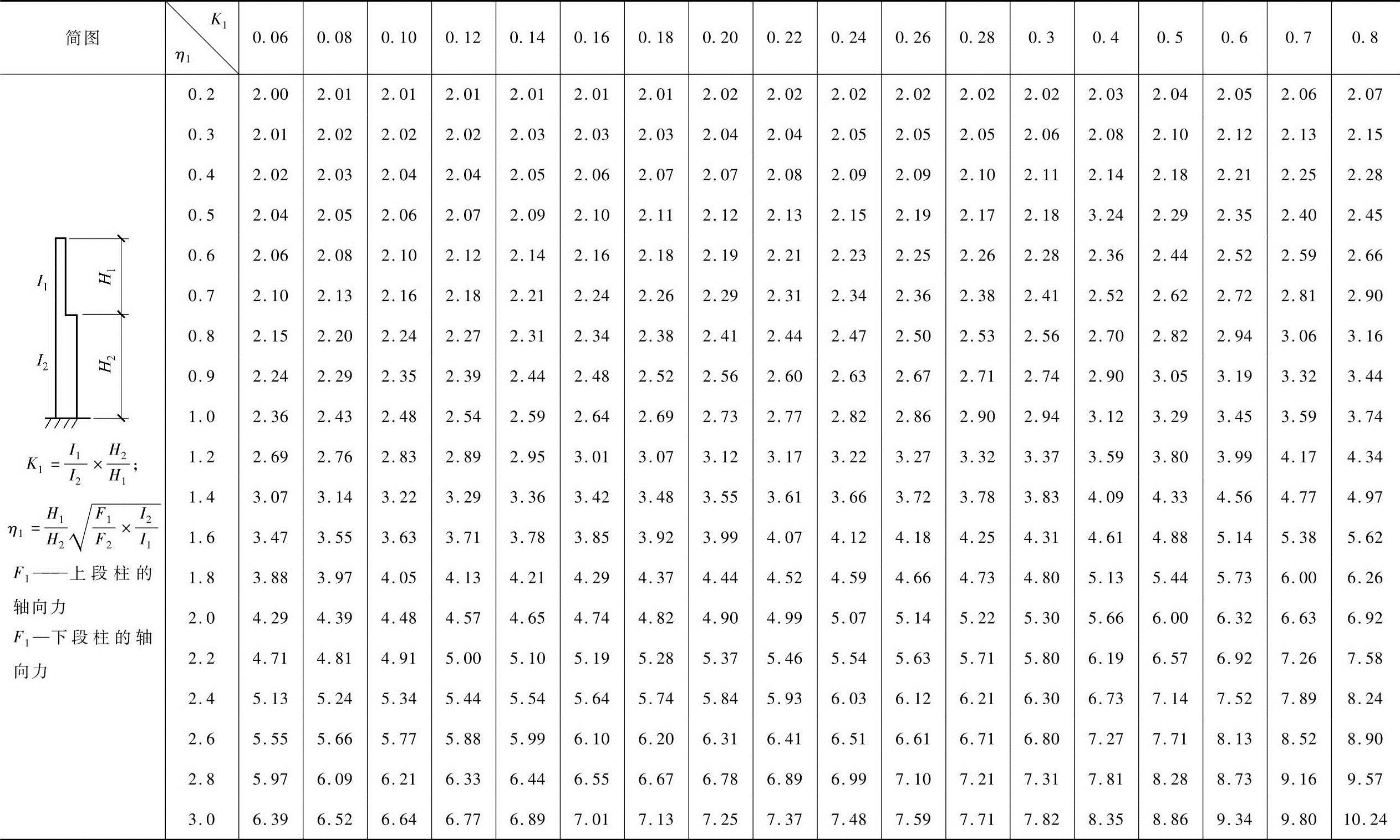
表2-28 柱上端可移动但不转动的单阶柱下段的计算长度系数μ2
注:表中的计算长度系数μ值按下式算得: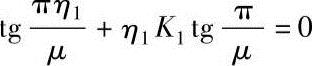
b.当柱上端与实腹梁刚接时,下段柱的计算长度系数μ2,应按下列公式计算的系数μ21乘以表2-27的折减系数。
当Kb<0.2时按下式计算,同时不大于按柱上端与横梁铰接计算时得到的μ2值。

当Kb≥0.2时按下式计算,但不小于按柱上端与横梁刚接计算时得到的μ2值。

式中 μ20——柱上端与横梁铰接时(即Kb=0时)单阶柱下段柱的计算长度系数;
μ2∞——柱上端与横梁刚接时(即Kb=∞时)单阶柱下段柱的计算长度系数;
η1——参数,按表2-26或表2-28中公式计算;
Kb——横梁线刚度与上段柱线刚度的比值,按式(2-72)计算:

K1——阶形柱上段柱线刚度与下段柱线刚度的比值,按式(2-73)计算:

Ib、lb——实腹钢梁的惯性矩和跨度;
I1、H1——阶形柱上段柱的惯性矩和柱高;
I2、H2——阶形柱下段柱的惯性矩和柱高。
c.上段柱的计算长度系数μ1,应按下式计算:

② 双阶柱
a.下段柱的计算长度系数μ3:当柱上端与横梁铰接时,等于按表2-29(柱上端为自由的双阶柱)的数值乘以表2-27的折减系数;当柱上端与横梁刚接时,等于按表2-30(柱上端可移动但不转动的双阶柱)的数值乘以表2-27的折减系数。
b.上段柱和中段柱的计算长度系数μ1和μ2,应按下列公式计算:

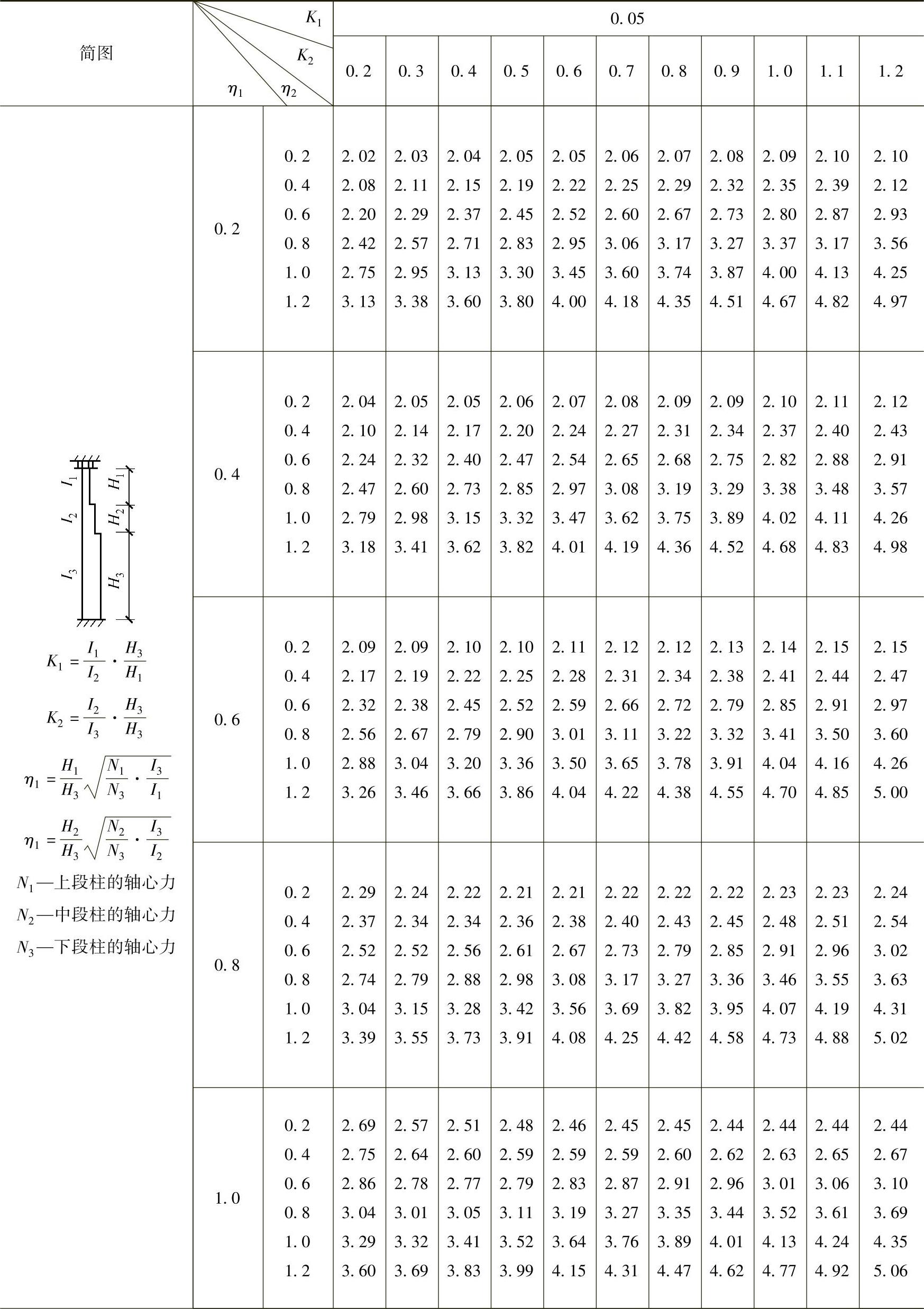
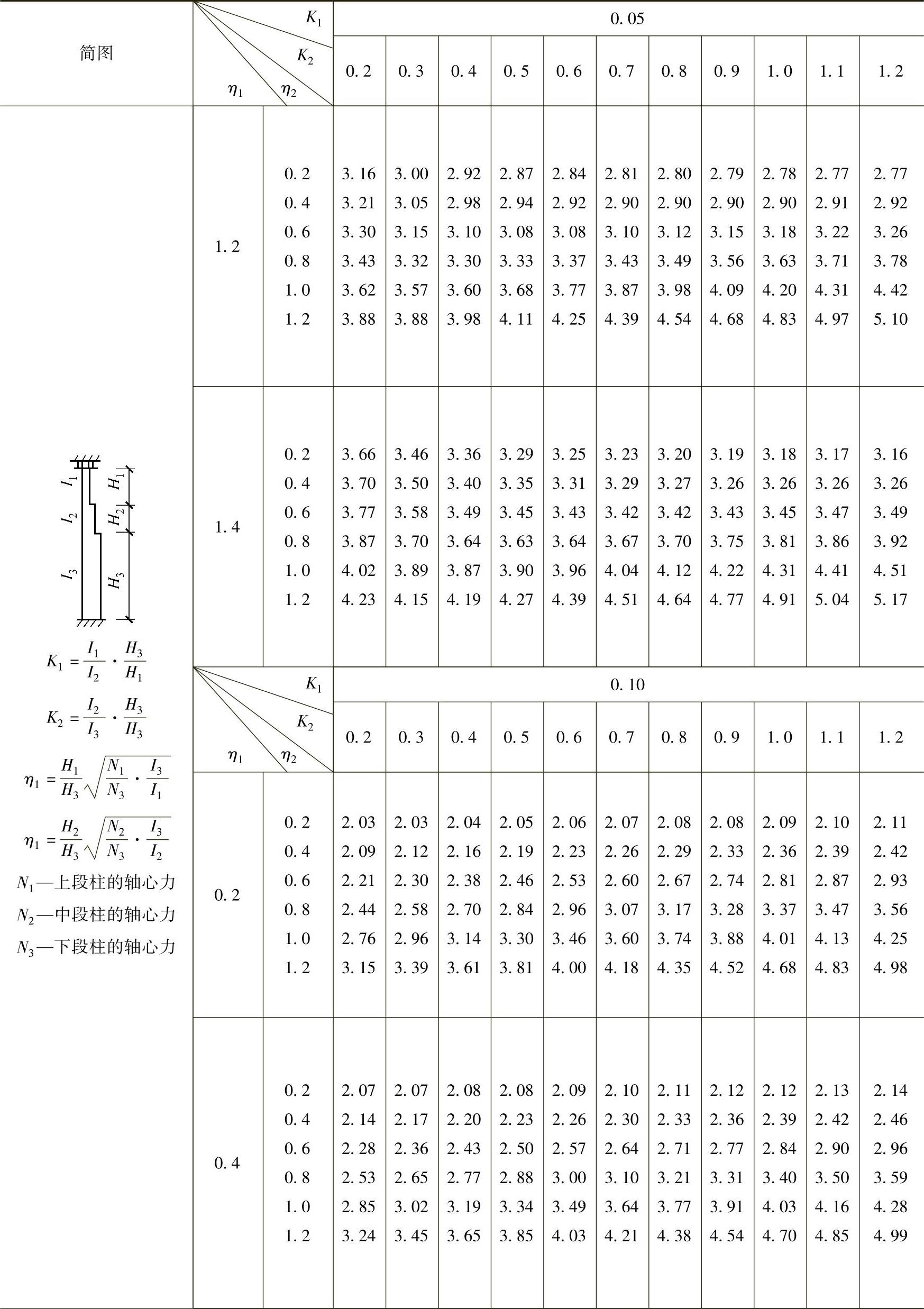
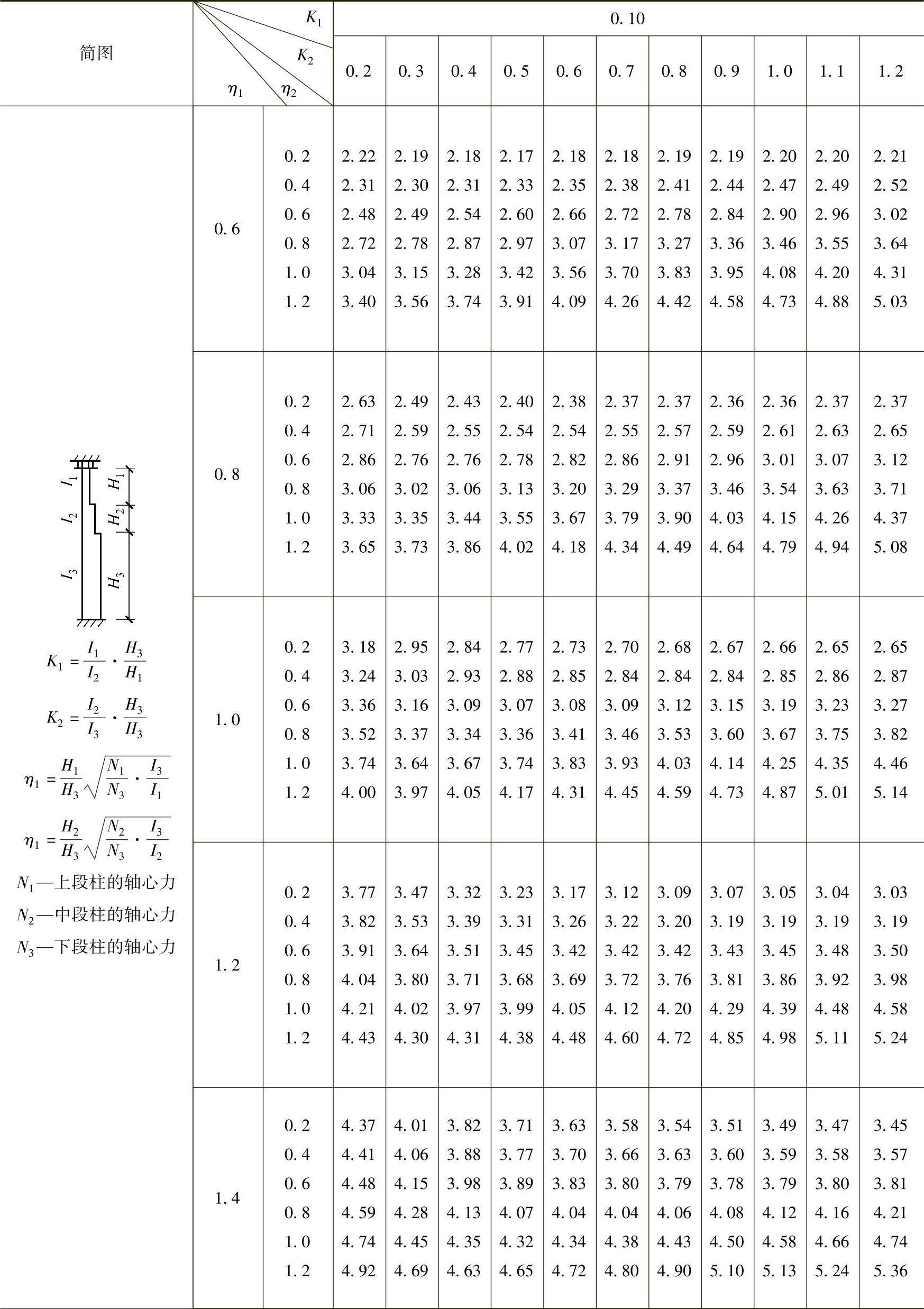
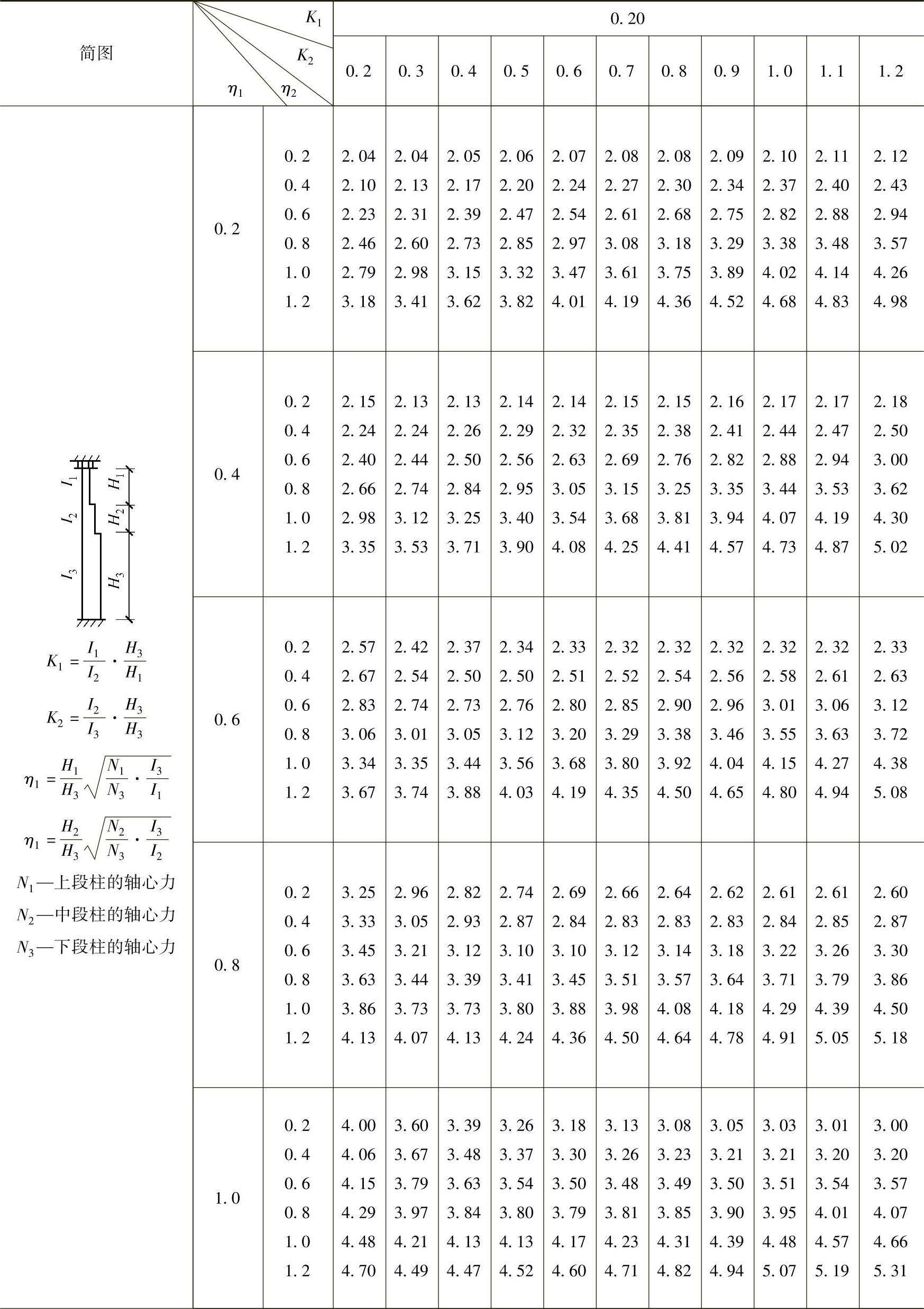
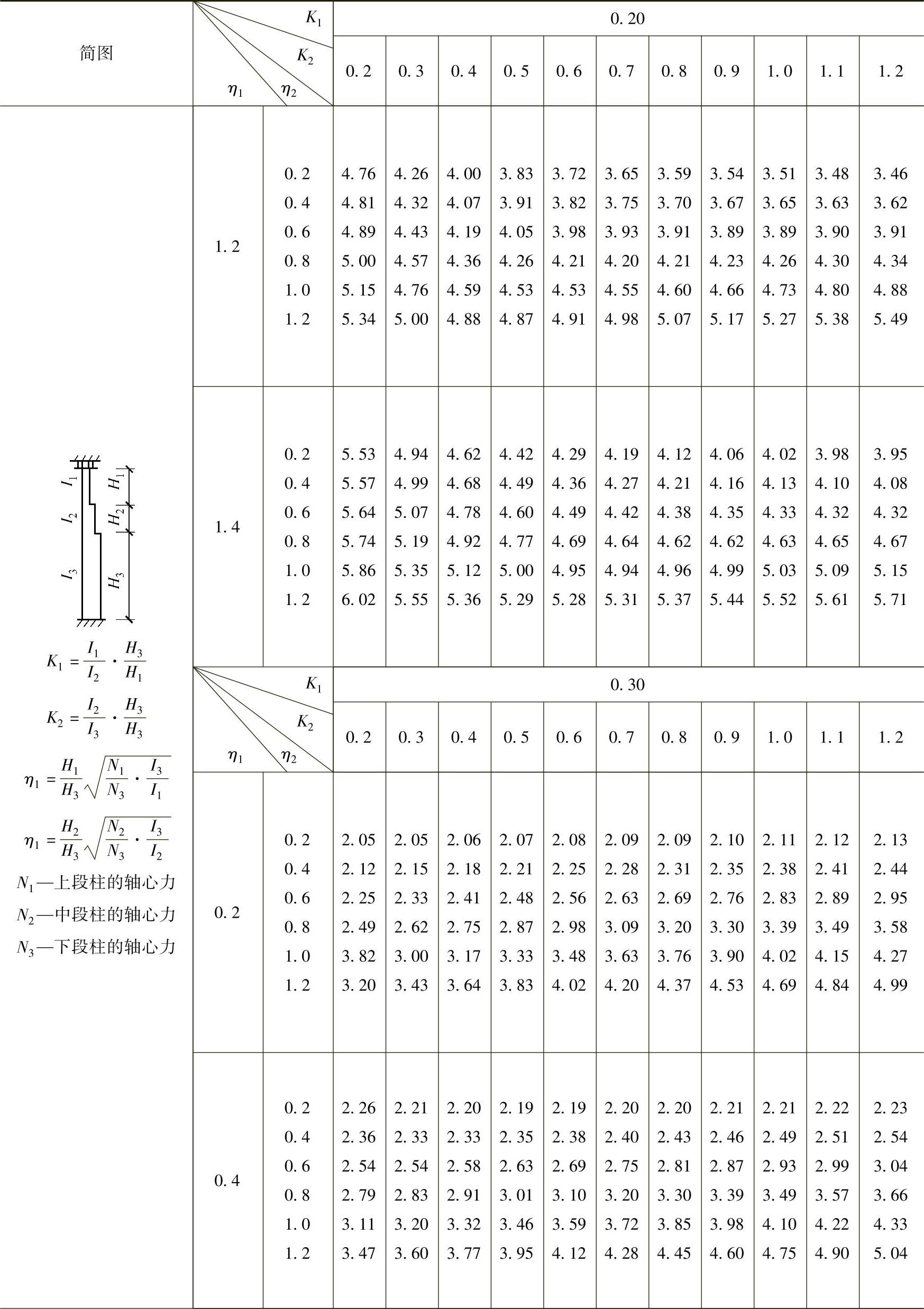
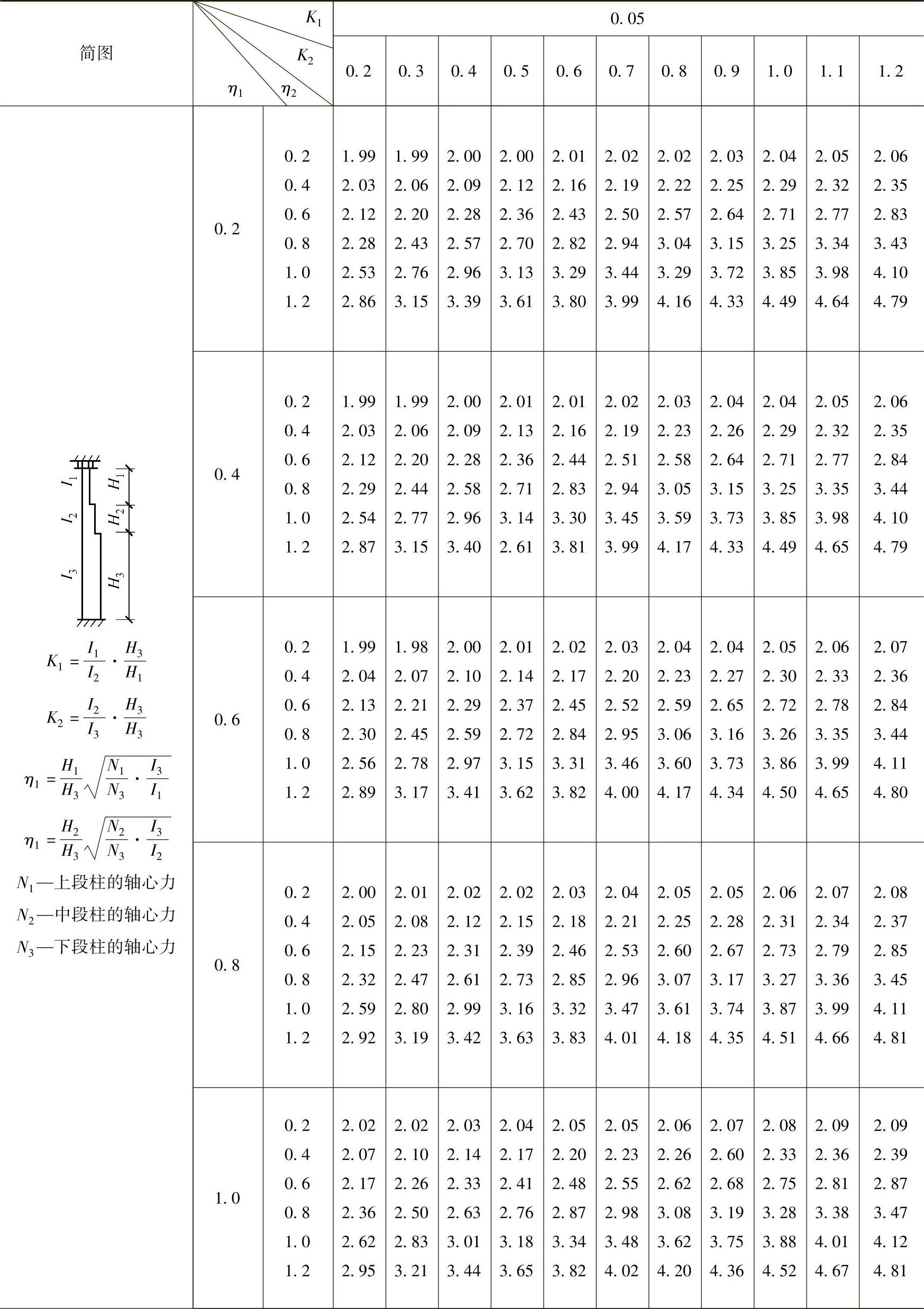
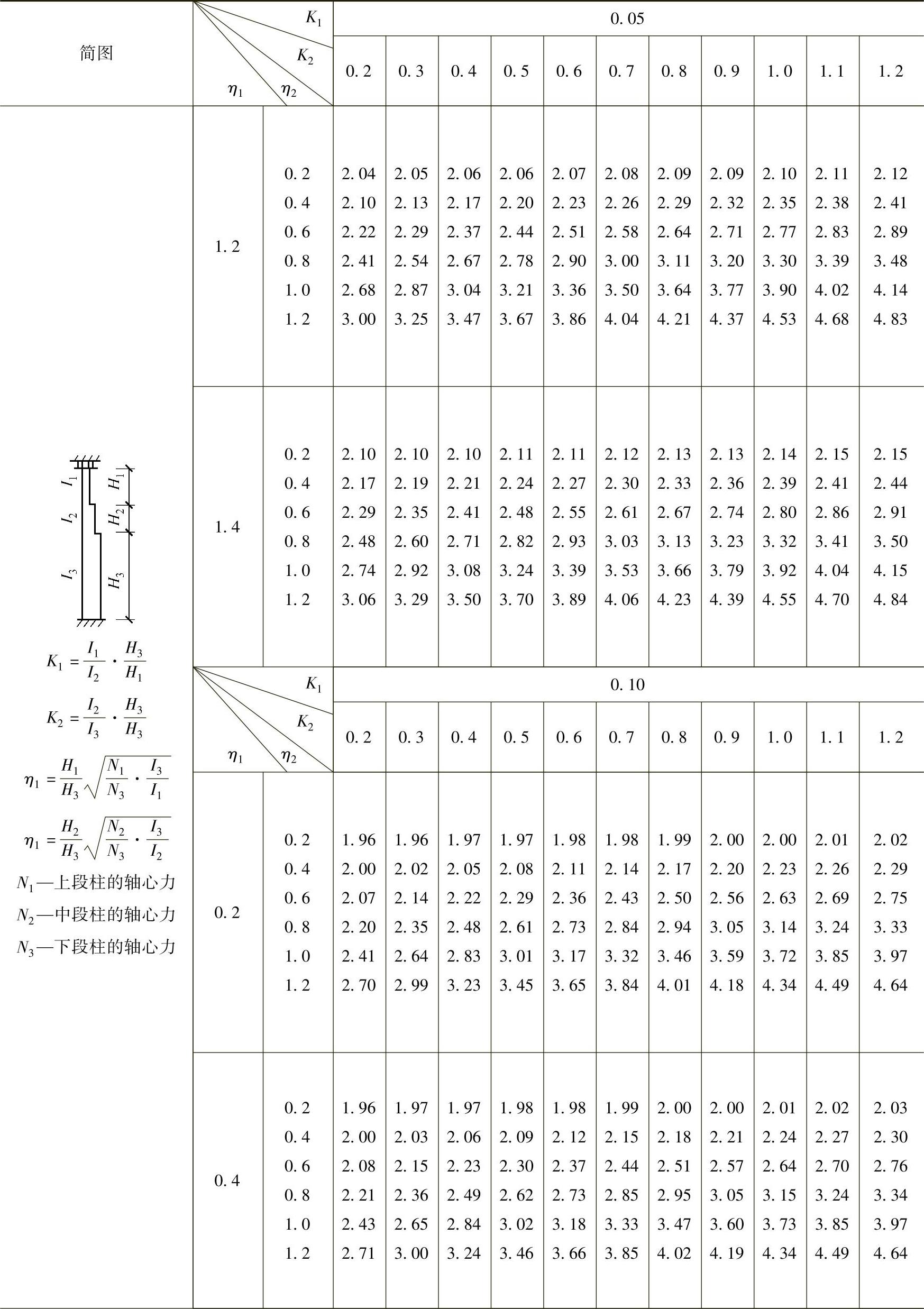
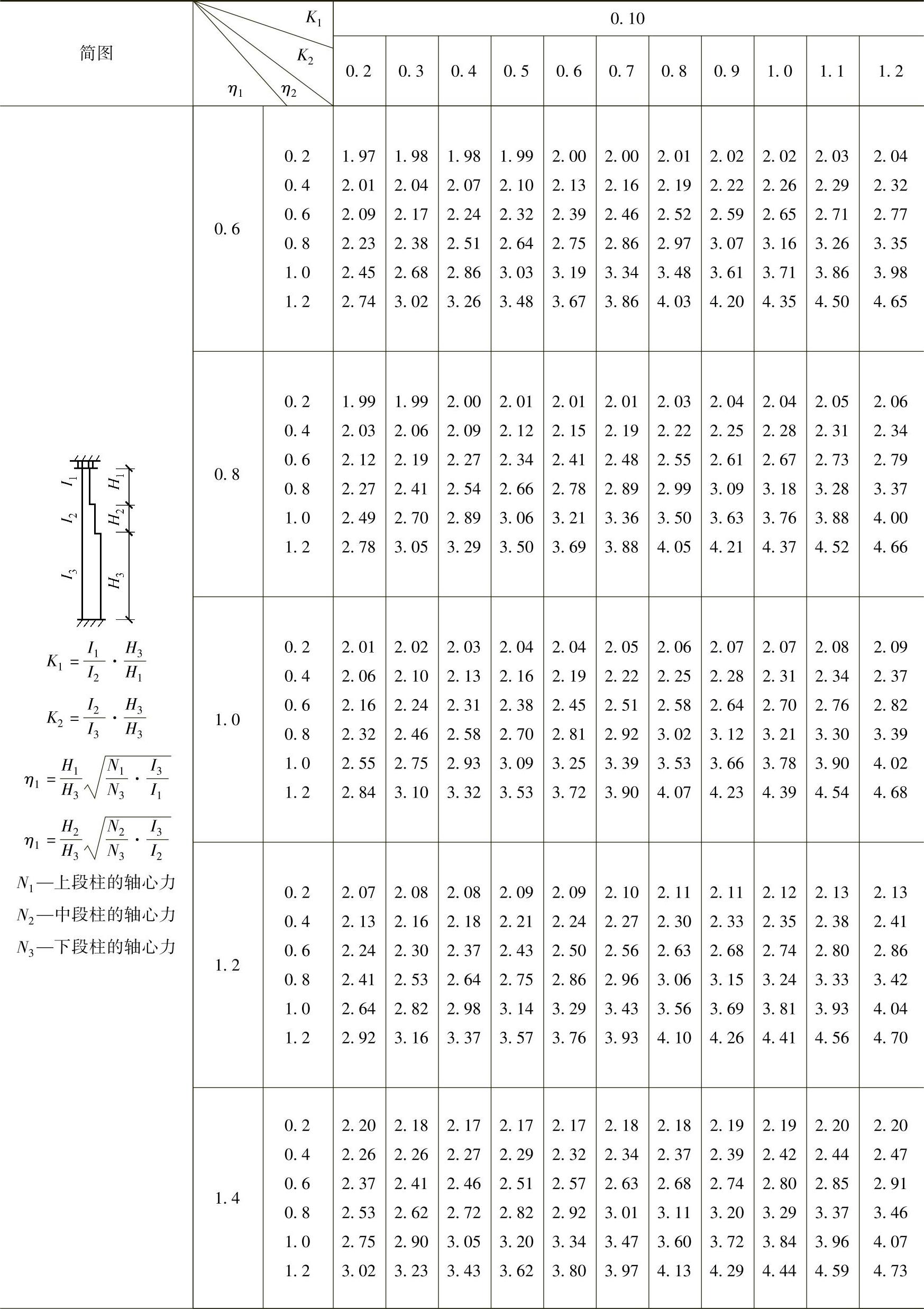
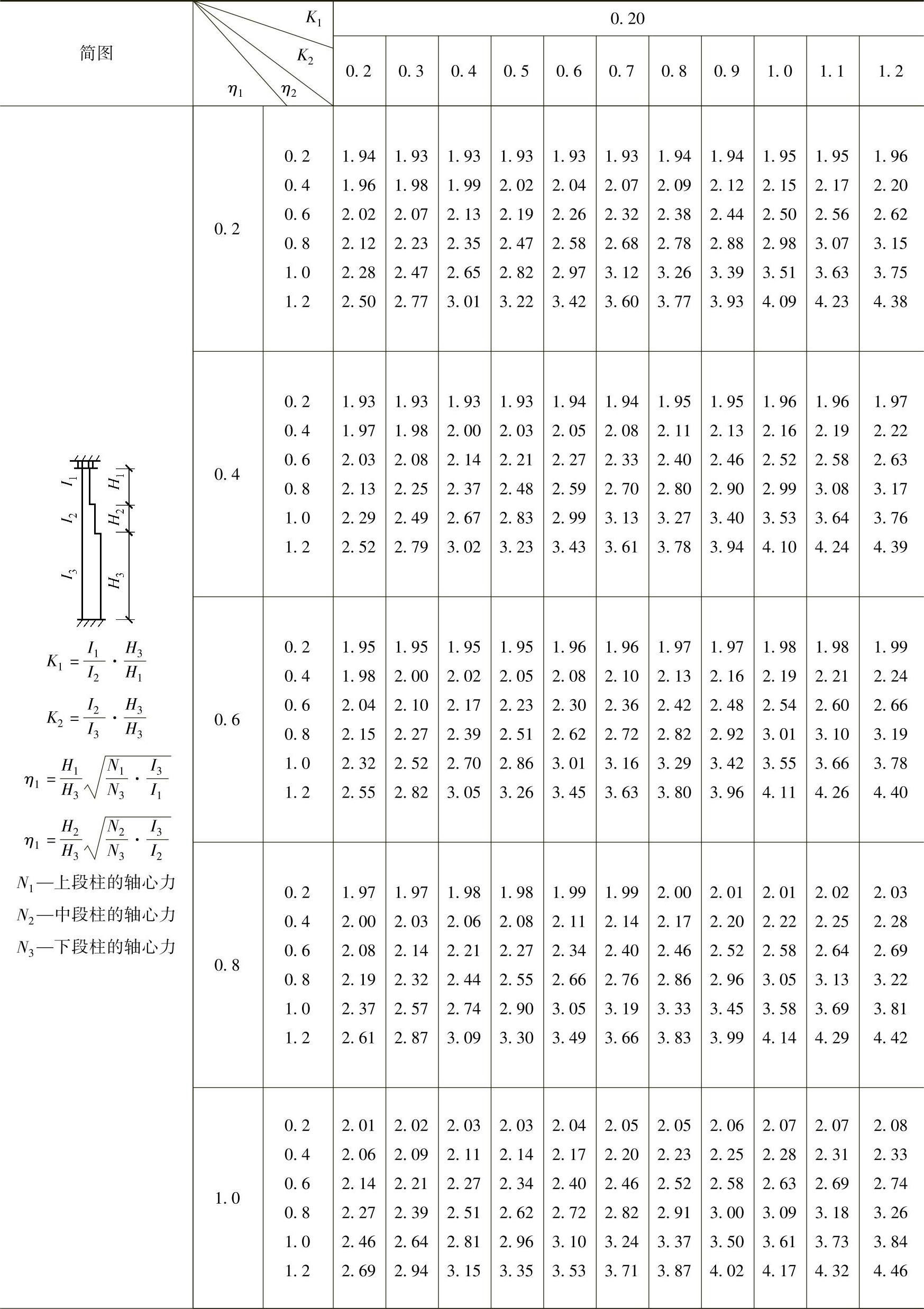
表2-29 柱上端为自由的双阶柱下段的计算长度系数μ3
(续)
(续)
(续)
(续)
(续)
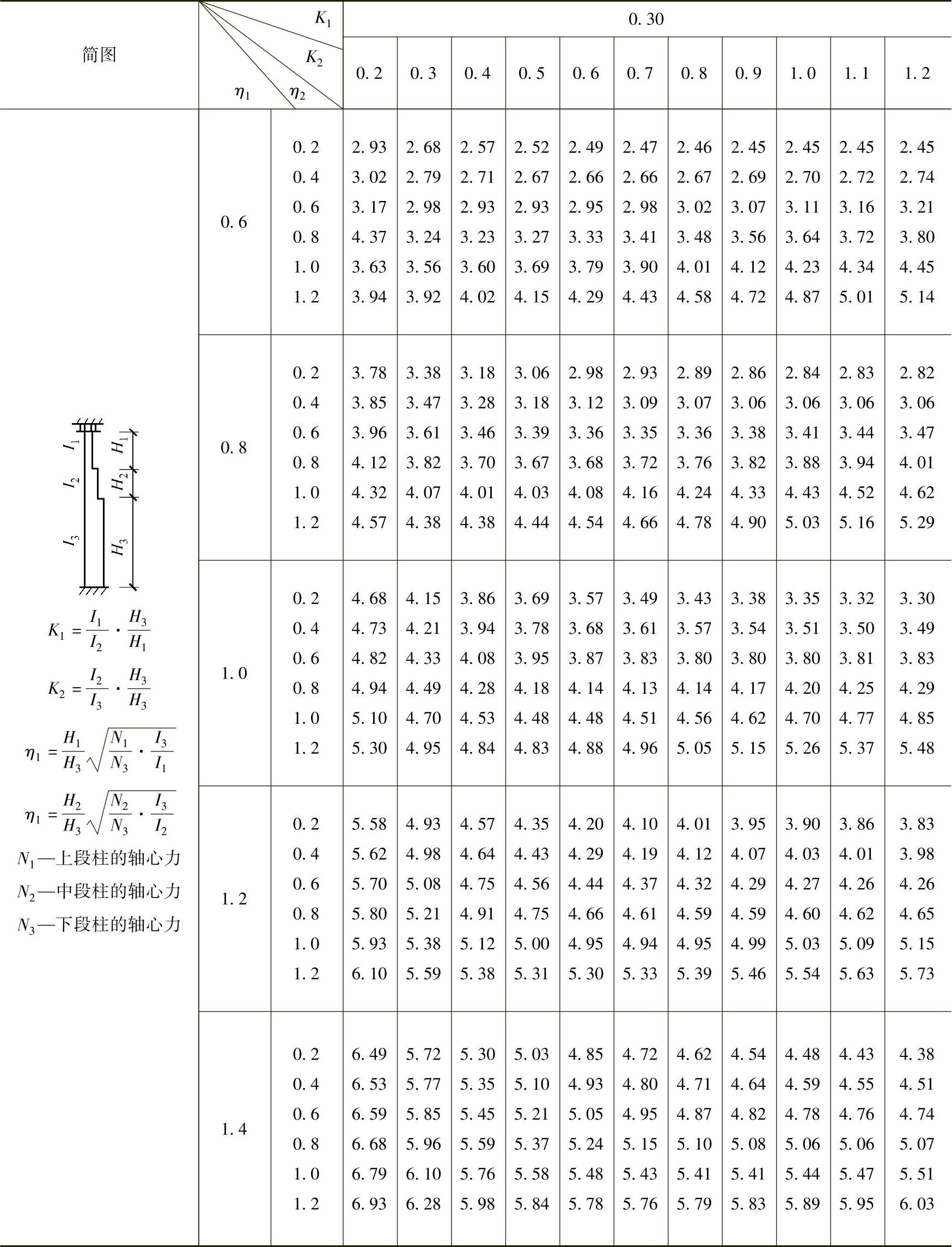
注:表中的计算长度系数μ3值系按下式算得: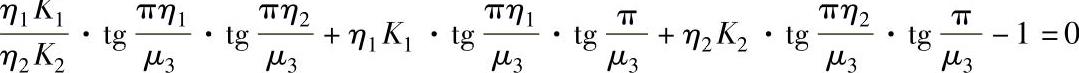
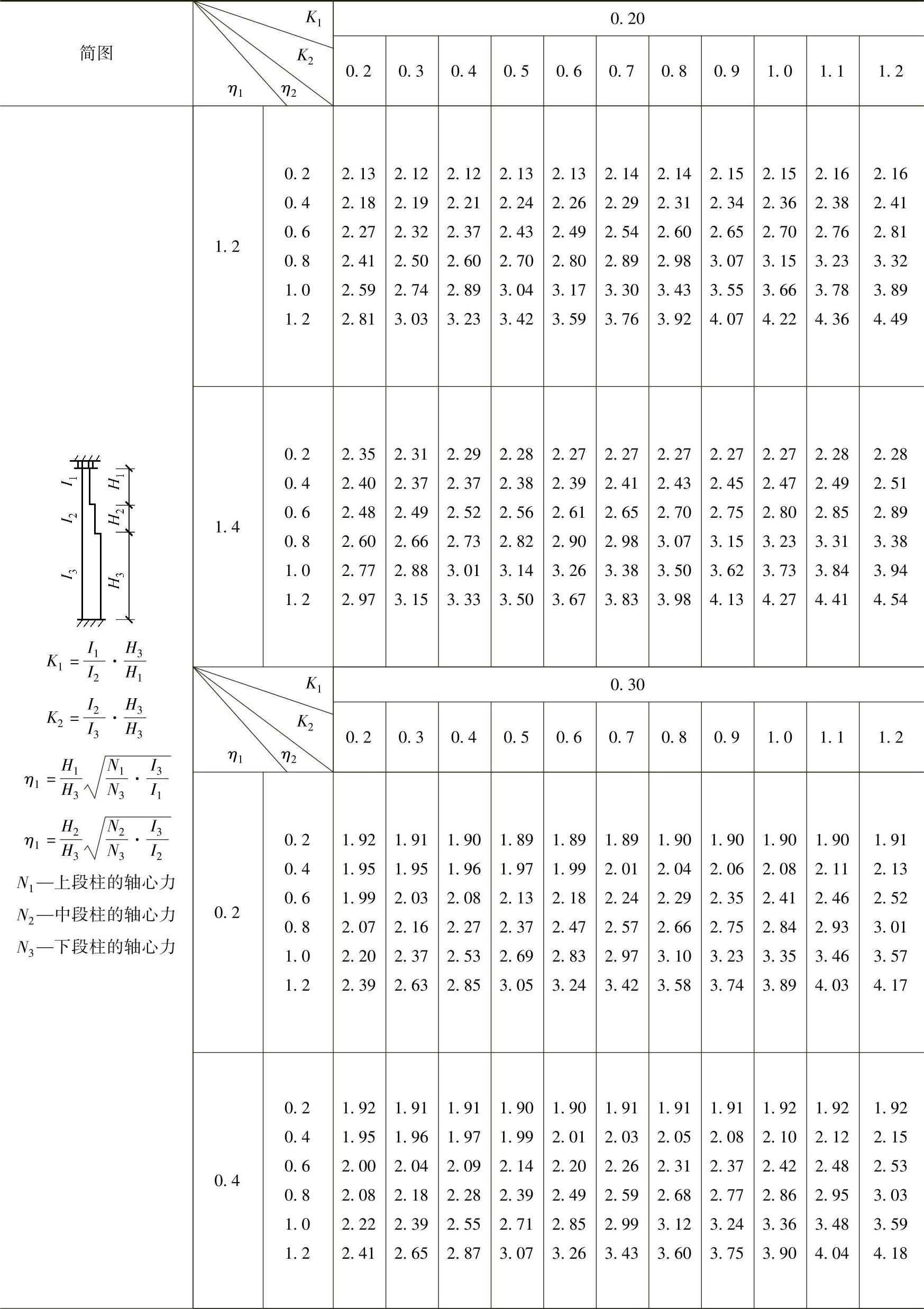
表2-30 柱顶可移动但不转动的双阶柱下段的计算长度系数μ3
(续)
(续)
(续)
(续)
(续)
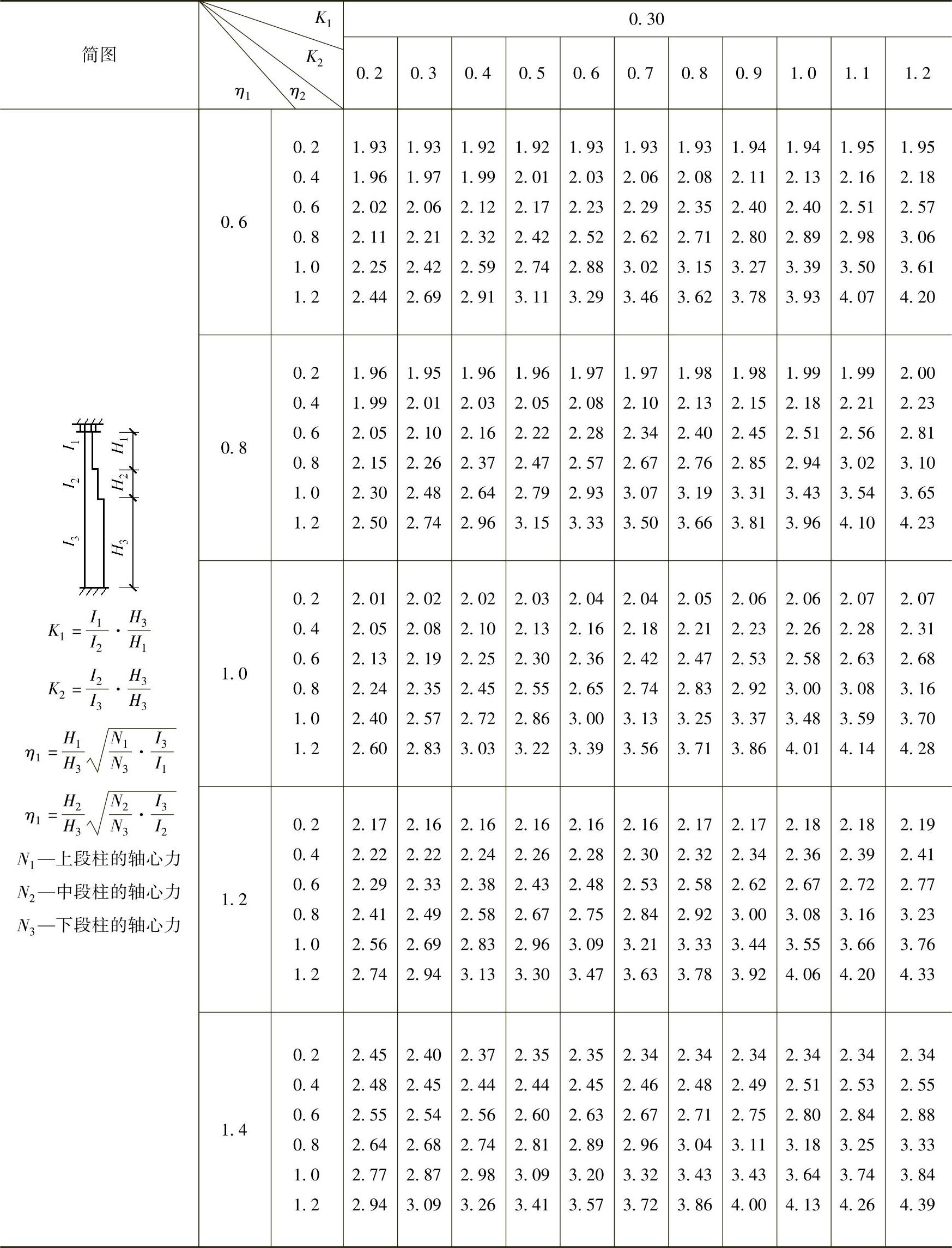
注:表中的计算长度系数μ3值按下式计算: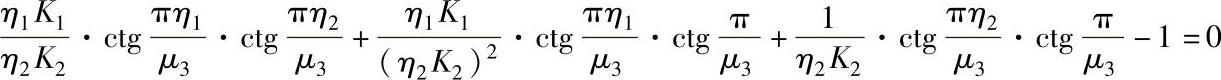
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




