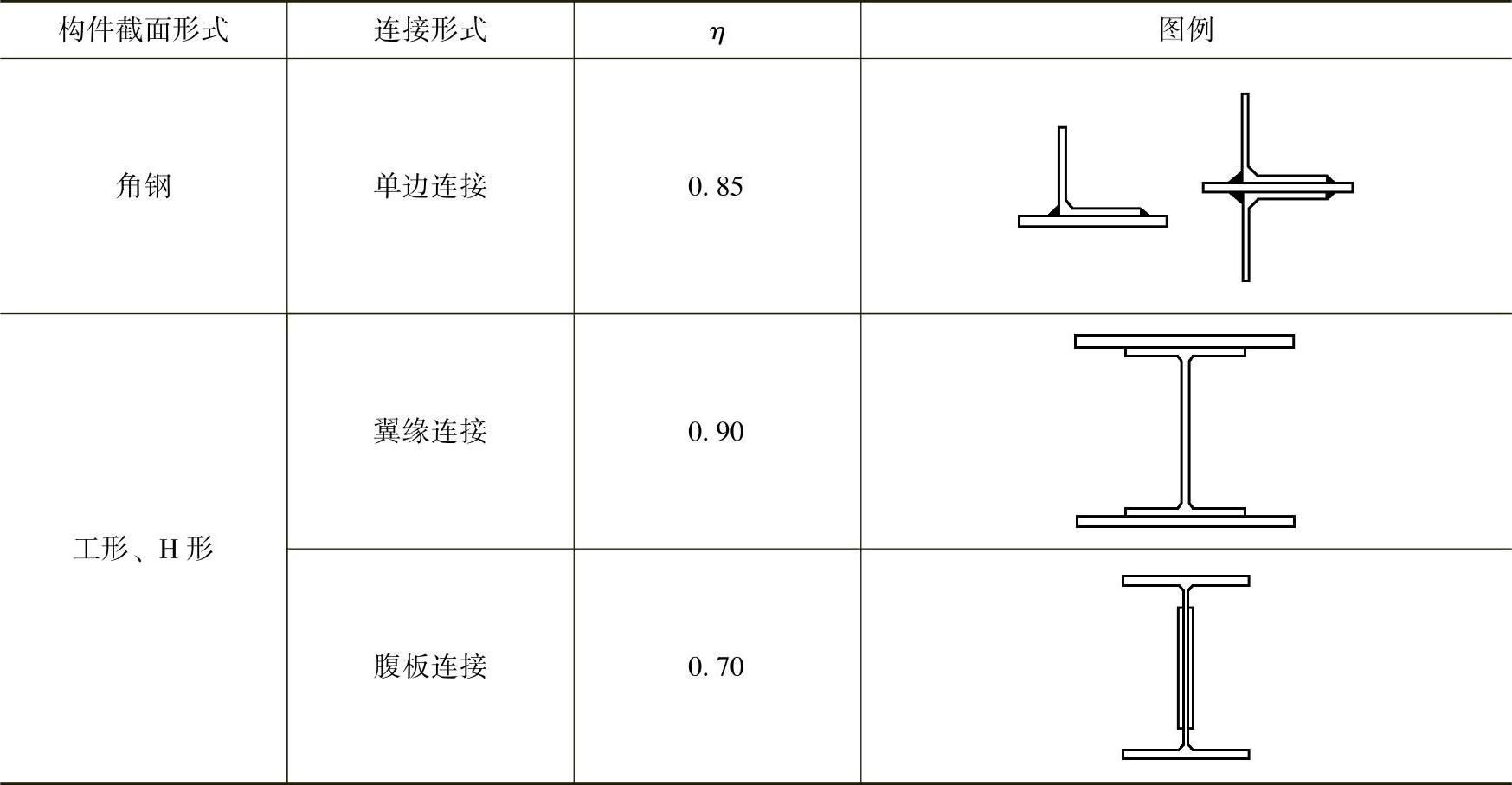
1)轴拉和轴压构件,当其组成板件在节点或拼接处并非全部直接传力时,应对危险截面的面积乘以有效截面系数η,不同构件截面形式和连接方式的η值应符合表2-13的规定。
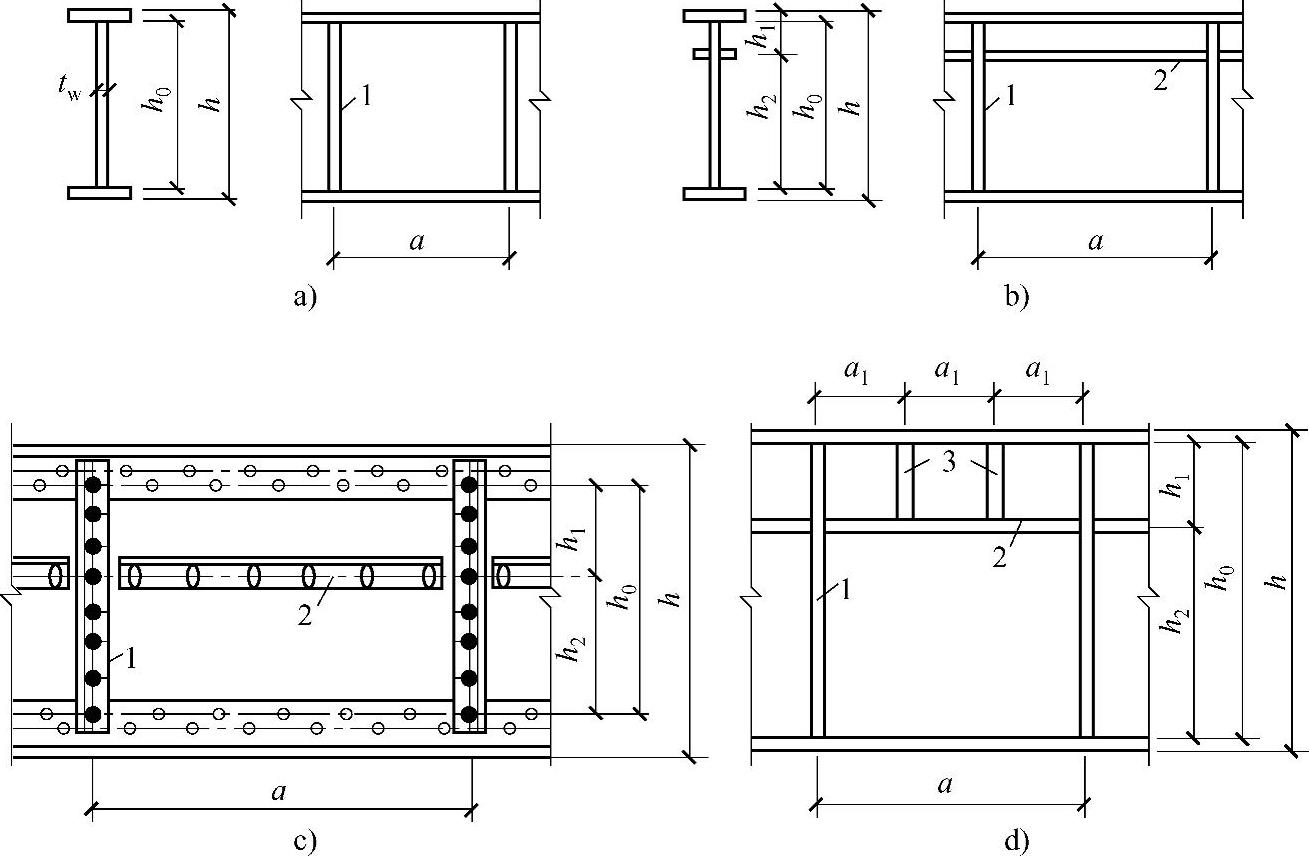
图2-4 加劲肋布置
a)仅配置横向加劲肋的腹板 b)用横向加劲肋和纵向加劲肋加强的腹板 c)用横向加劲肋和纵向加劲肋加强的腹板 d)在受压翼缘与纵向加劲肋之间设有短加劲肋的区格
1—横向加劲肋 2—纵向加劲肋 3—短加劲肋
表2-13 轴心受力构件节点或拼接处危险截面有效截面系数
2)轴压构件的稳定性应按下式计算:

式中 φ——轴心受压构件的稳定系数(取截面两主轴稳定系数中的较小者),根据构件的长细比(或换算长细比)、钢材屈服强度和表2-14、表2-15的截面分类,按表2-16~表2-20采用。
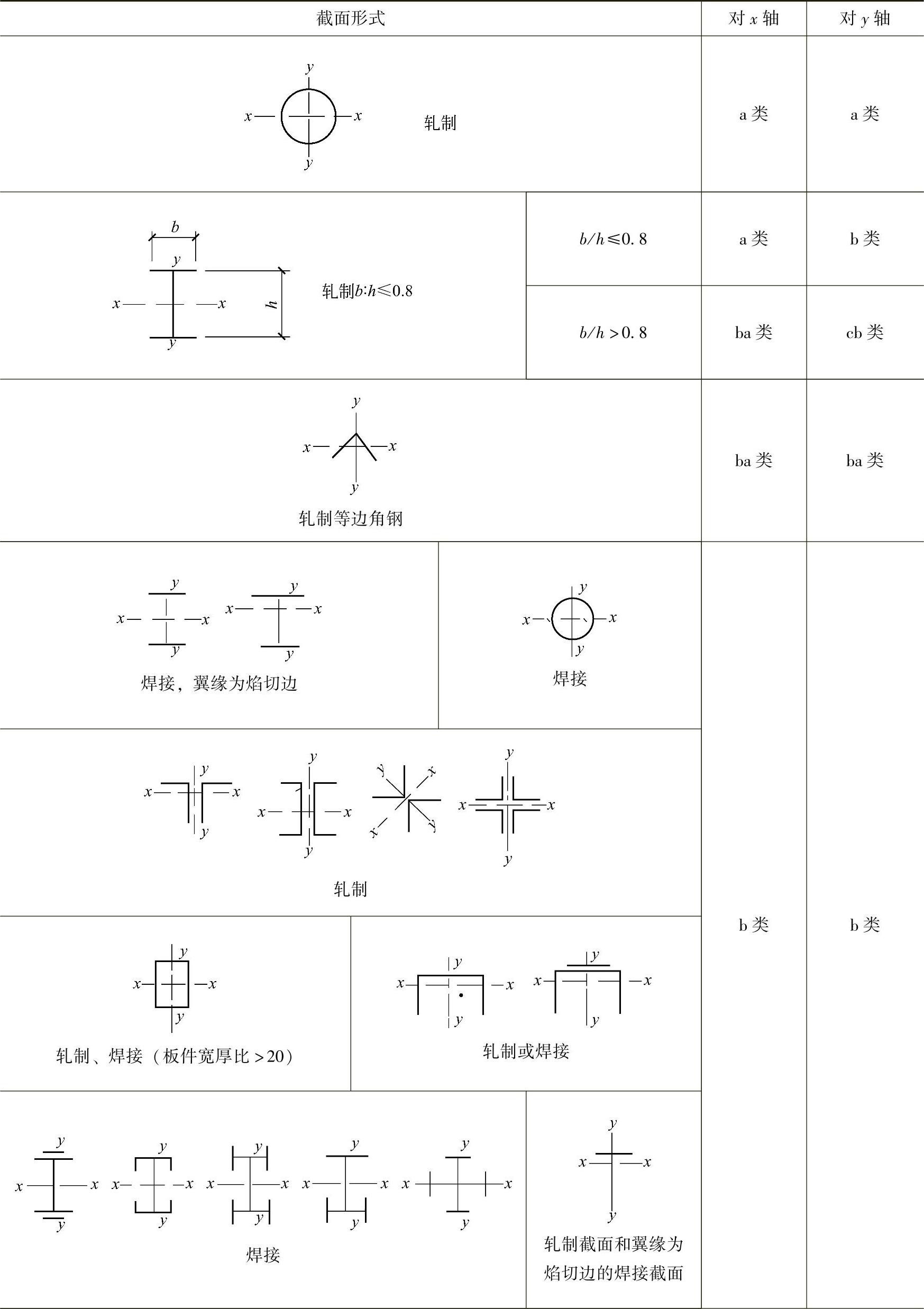
表2-14 轴心受压构件的截面分类(板厚t<40mm)
(续)
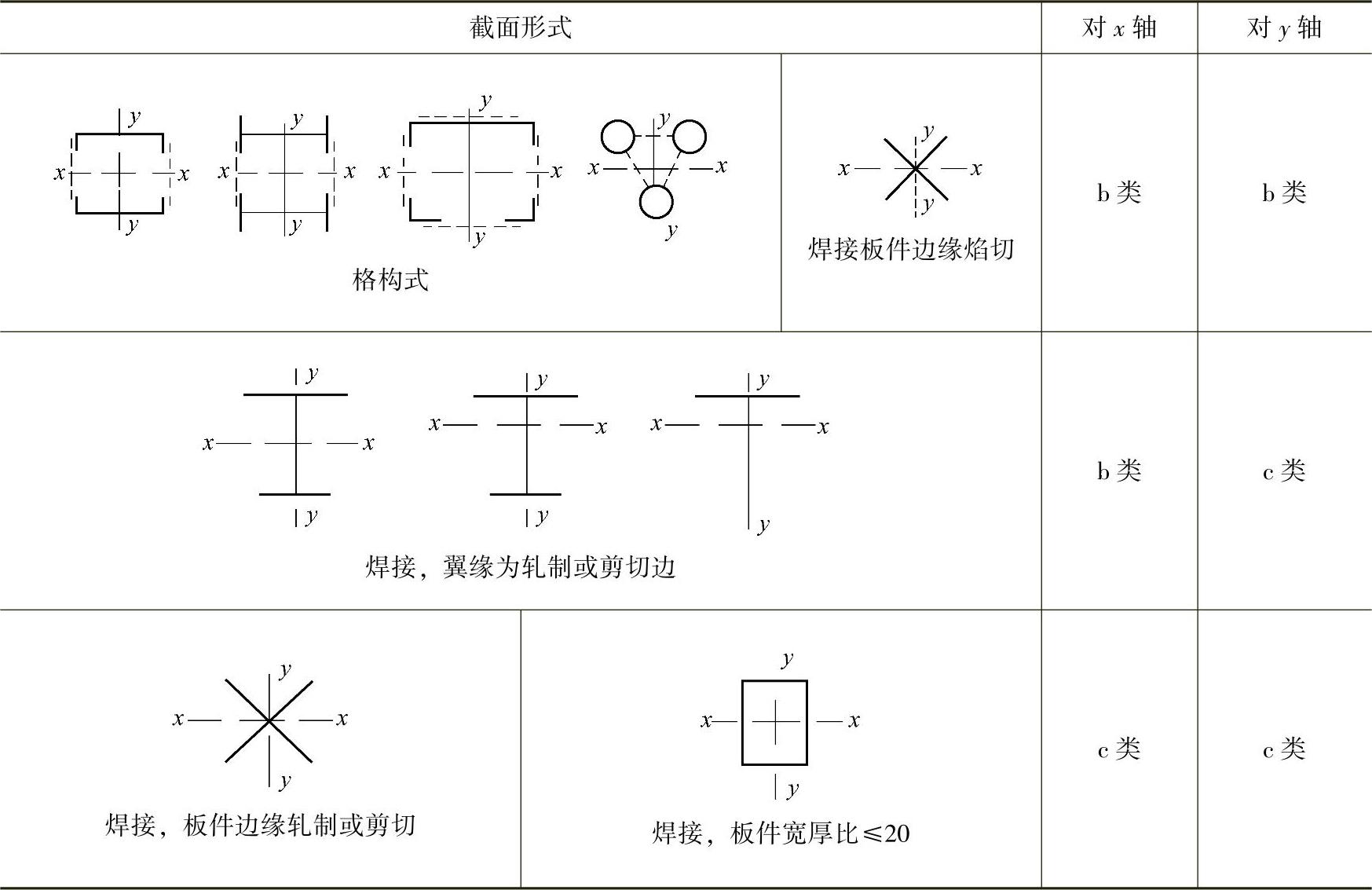
注:ba类含义为Q235钢取b类,Q345、Q390、Q420和Q460取a类;cb类含义为Q235钢取c类,Q345、Q390、Q420和Q460取b类。
表2-15 轴心受压构件的截面分类(板厚t≥40mm)
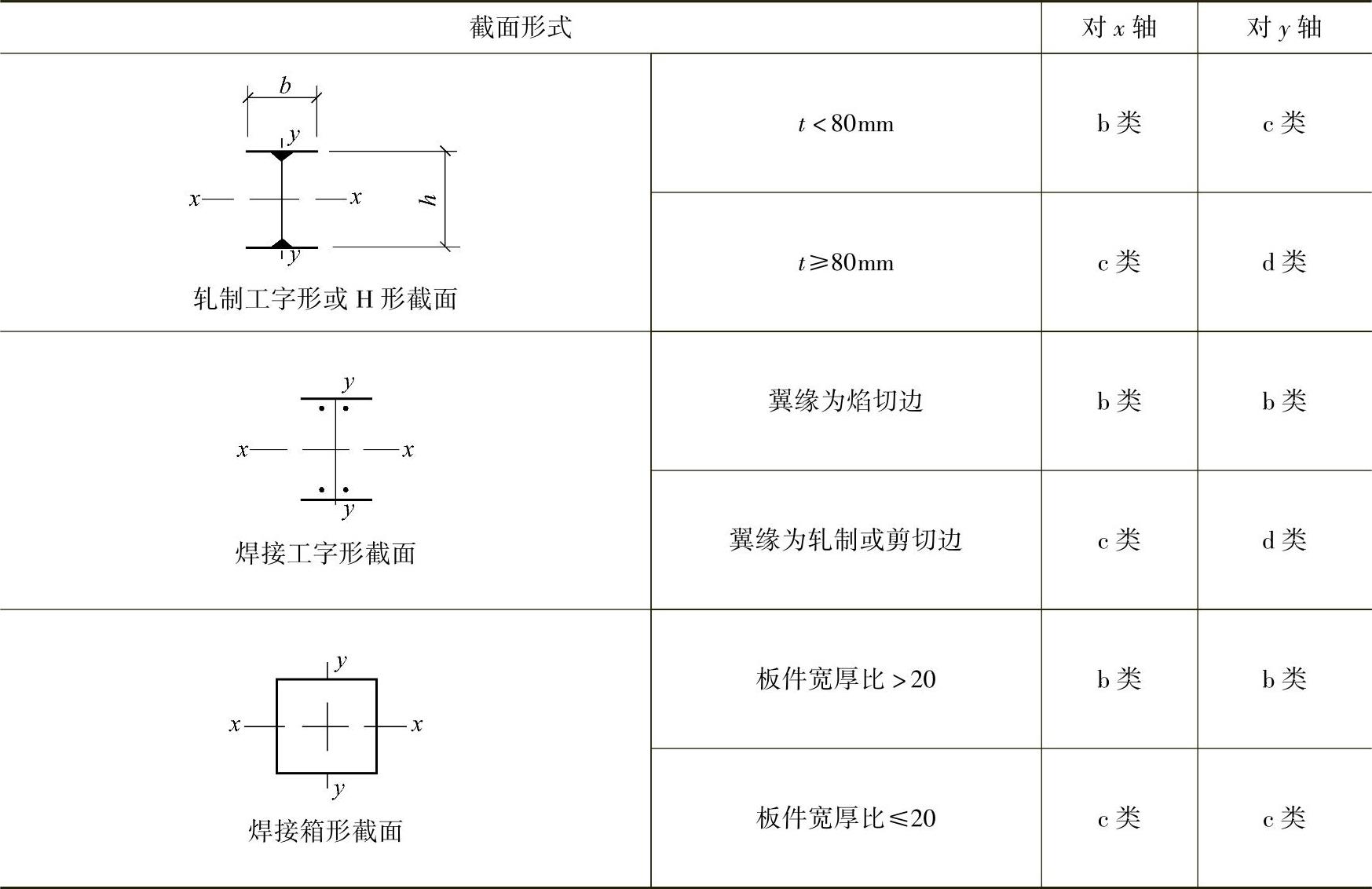
表2-16 a类截面轴心受压构件的稳定系数φ
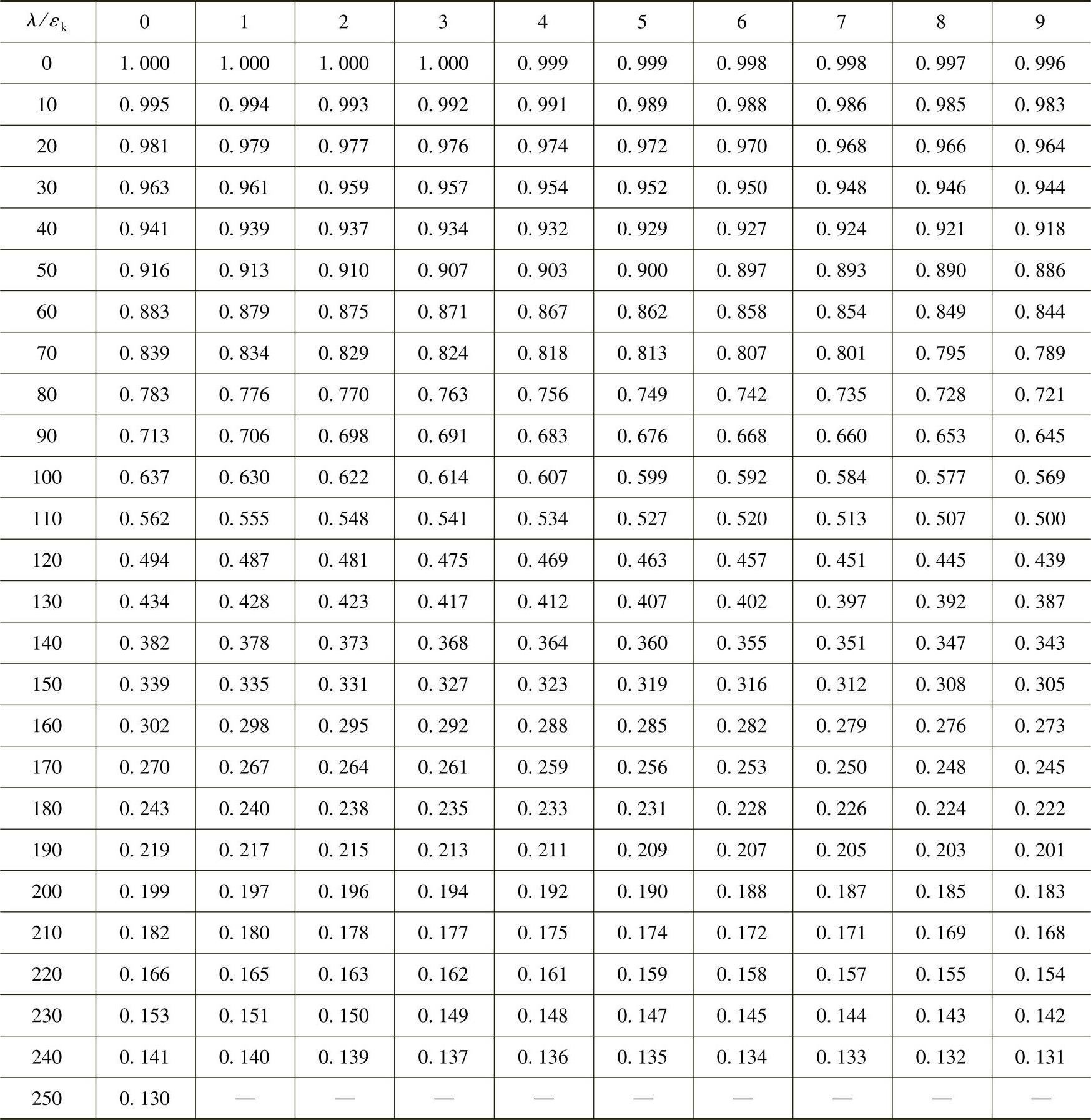
注:见表2-19注。
表2-17 b类截面轴心受压构件的稳定系数φ
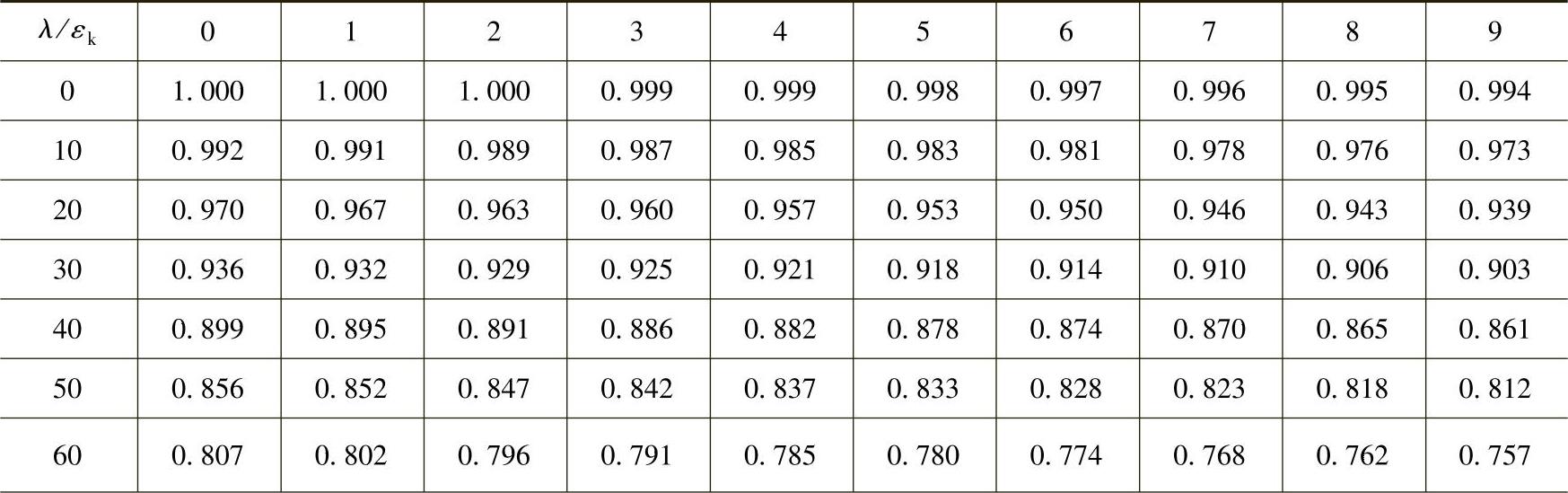
(续)
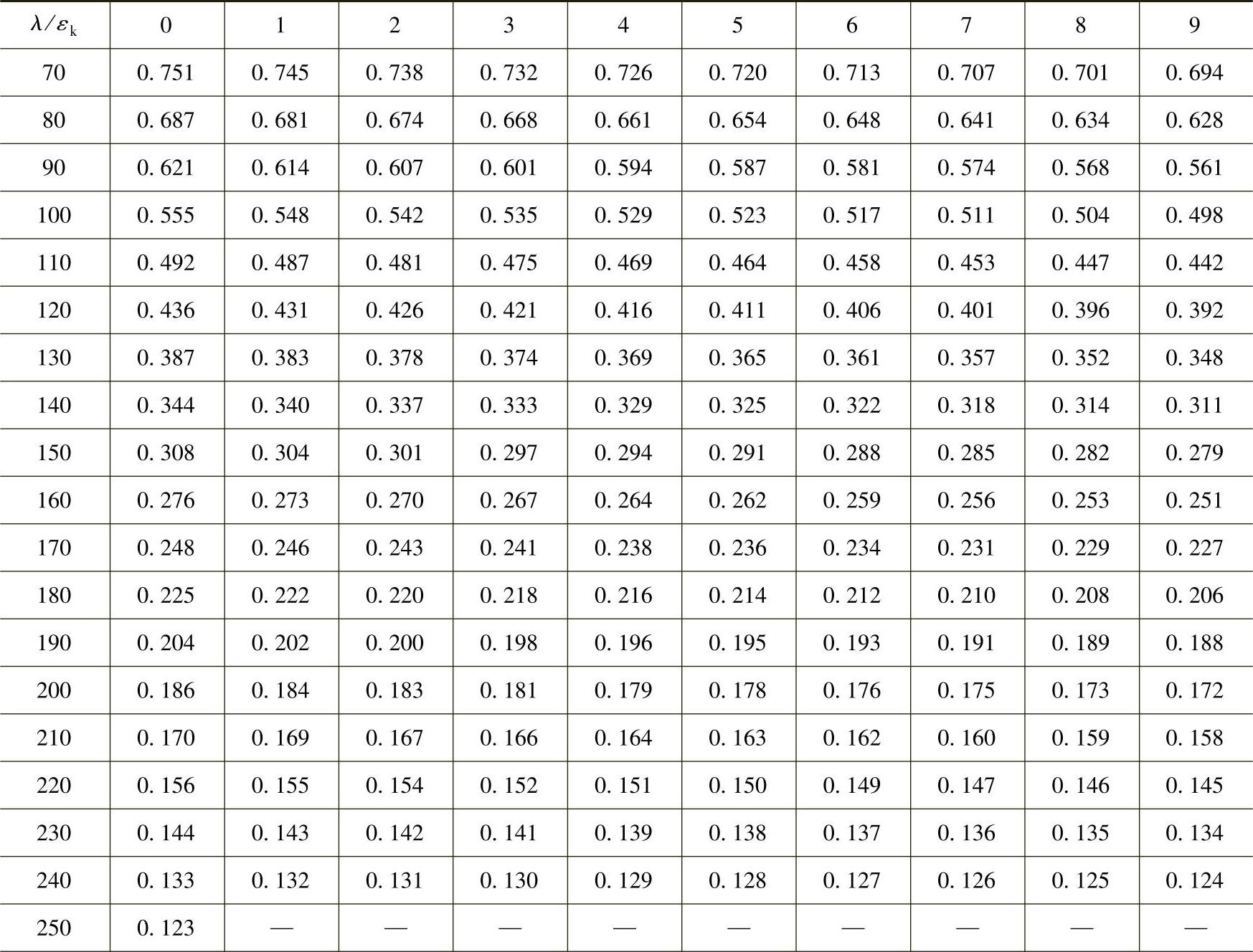
注:见表2-19注。
表2-18 c类截面轴心受压构件的稳定系数φ
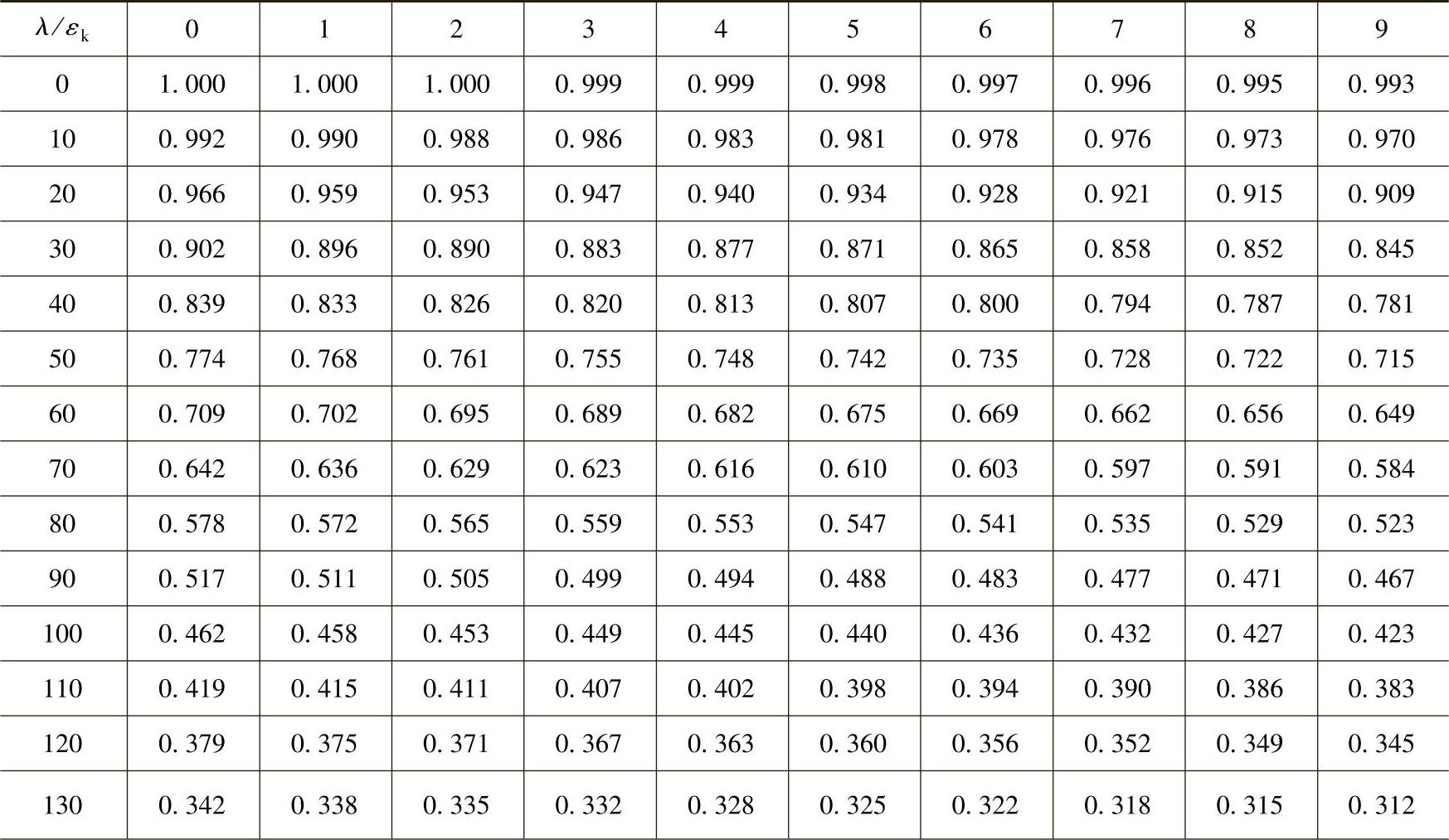
(续)
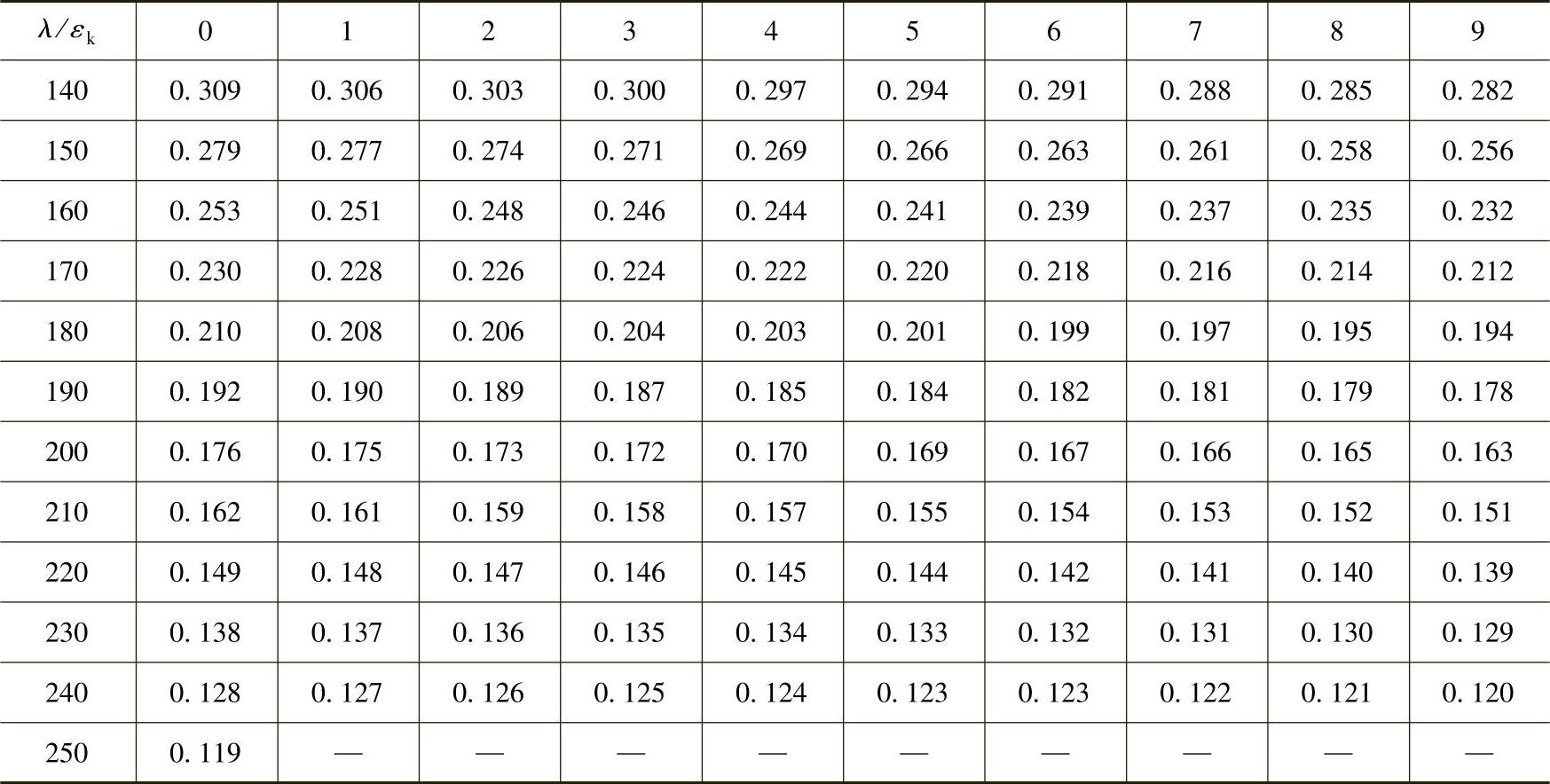
注:见表2-19注。
表2-19 d类截面轴心受压构件的稳定系数φ
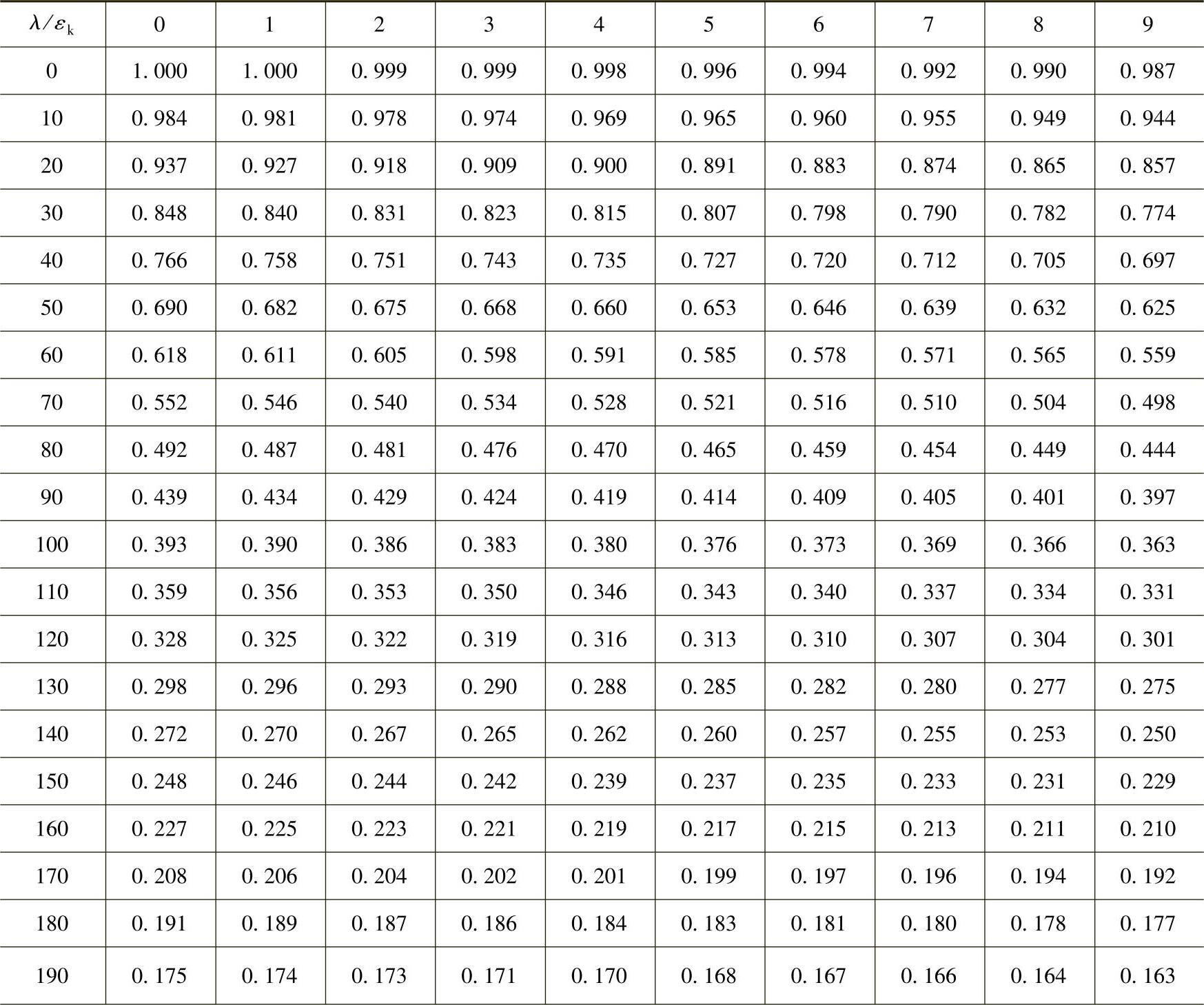
(续)

注:1.本表中的φ值按下列公式计算:
当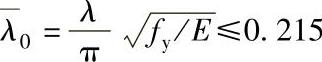 时:
时: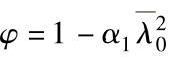
当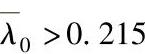 时:
时: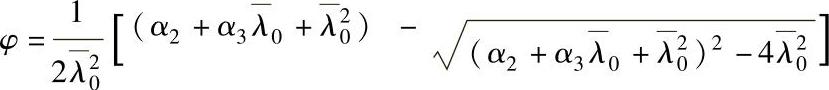
2.当构件的λ/εk值超出本表的范围时,则φ值按注1所列的公式计算。
表2-20 系数α1、α2、α3
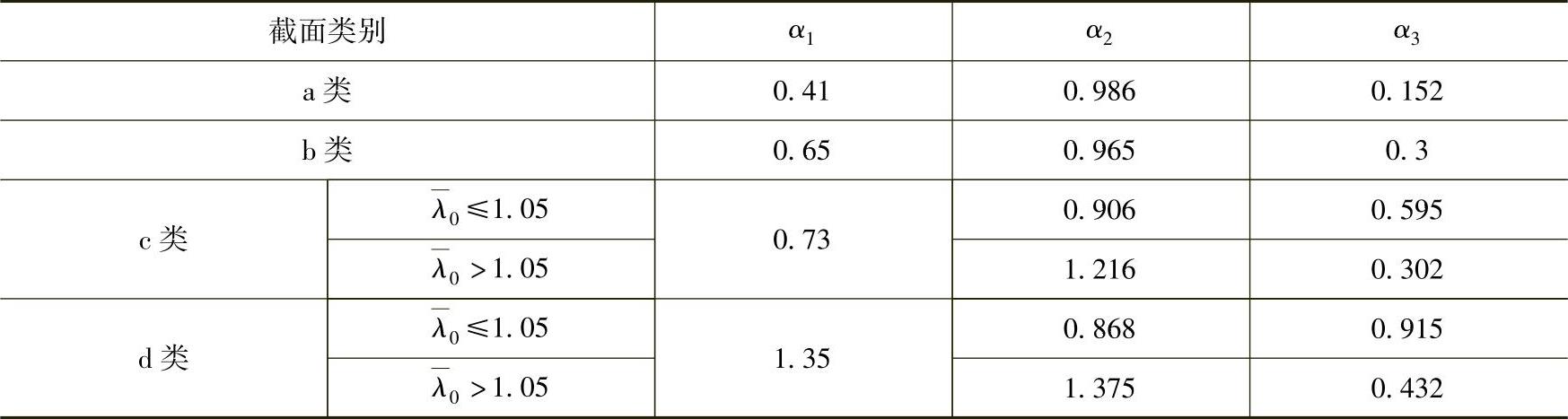
3)实腹式构件的长细比λ应根据其失稳模式,由下列各款确定:
① 截面形心与剪心重合的构件
a.当计算弯曲屈曲时长细比按下式计算:

式中 l0x、l0y——分别为构件对截面主轴x和y的计算长度;
ix、iy——分别为构件截面对主轴x和y的回转半径。
b.当计算扭转屈曲时,长细比按下式计算:

式中 I0、It、Iw——构件毛截面对剪心的极惯性矩、截面抗扭惯性矩和扇性惯性矩,对十字形截面可近似取Iw=0;
lw——扭转屈曲的计算长度,两端铰支且端截面可自由翘曲者,取几何长度l;两端嵌固且端部截面的翘曲完全受到约束者,取0.5l。
对轴对称十字形截面板件宽厚比不超过15εk者,可不计算扭转屈曲。
② 截面为单轴对称的构件
a.绕非对称主轴的弯曲屈曲,长细比应由式(2-9)、式(2-10)确定。绕对称轴主轴的弯扭屈曲,应取下式给出的换算长细比:
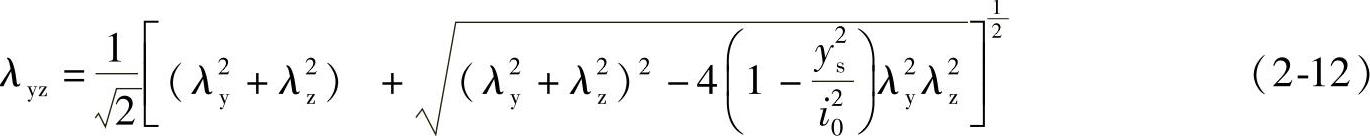
式中 ys——截面形心至剪心的距离;
i0——截面对剪心的极回转半径,单轴对称截面i20=y2s+i2x+i2y;
λz——扭转屈曲换算长细比,由式(2-11)确定。
b.双角钢组合T形截面构件绕对称轴的换算长细比λyz可用下列简化公式确定:
ⓘ 等边双角钢(图2-5a)
当λy>λz时:

当λy<λz时:

 长肢相并的不等边双角钢(图2-5b)
长肢相并的不等边双角钢(图2-5b)
当λy>λz时:

当λy<λz时:

 短肢相并的不等边双角钢(图2-5c)
短肢相并的不等边双角钢(图2-5c)
当λy>λz时:

当λy<λz时:

③ 截面无对称轴且剪心和形心不重合的构件,应采用下列换算长细比:

式中 Nxyz——弹性完善杆的弯扭屈曲临界力,应按下式计算:
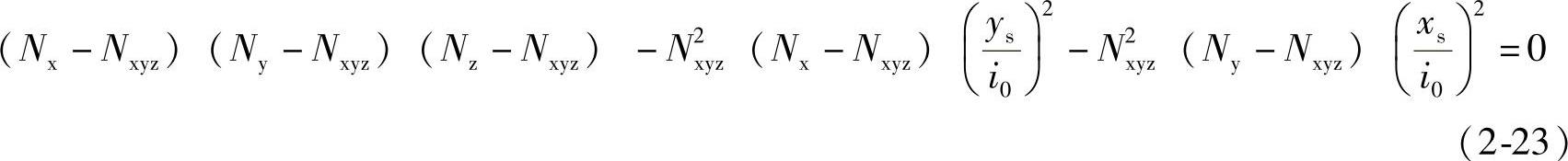
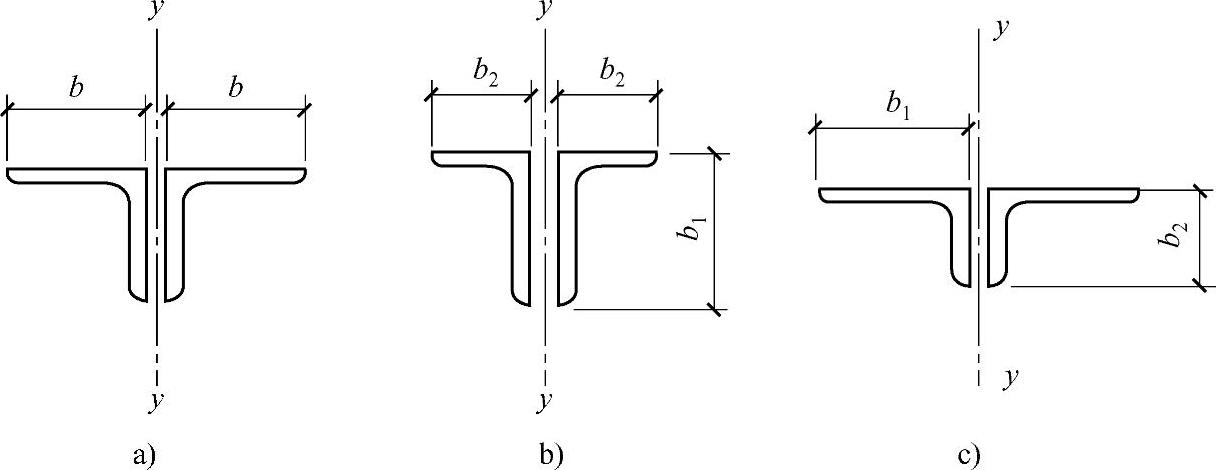
图2-5 单角钢截面和双角钢组合T形截面
a)等边双角钢 b)长肢相并的不等边双角钢 c)短肢相并的不等边双角钢
b—等边角钢肢宽度 b1—不等边角钢长肢宽度 b2—不等边角钢短肢宽度
xs、ys——截面剪心的坐标;
i0——截面对剪心的极回转半径,应按下式计算:
i20=i2x+i2y+x2s+y2s (2-24)
Nx、Ny、Nz——分别为绕x轴和y轴的弯曲屈曲临界力和扭转屈曲临界力,应按下列公式计算:
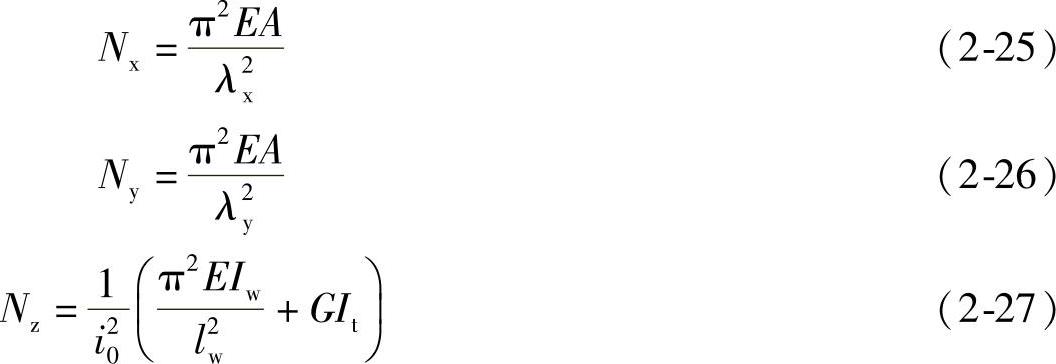
E、G——分别为钢材弹性模量和剪变模量。
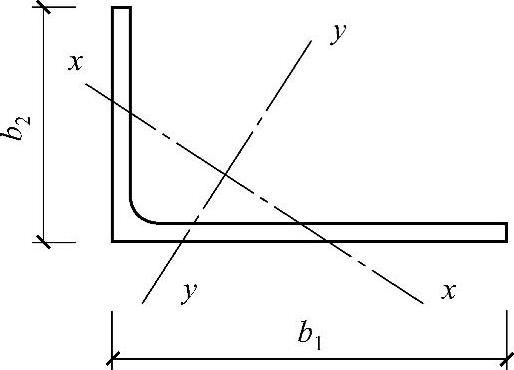
④ 不等边角钢轴压构件的换算长细比可用下列简化公式确定(图2-6):
当λx>λz时:

当λx<λz时:
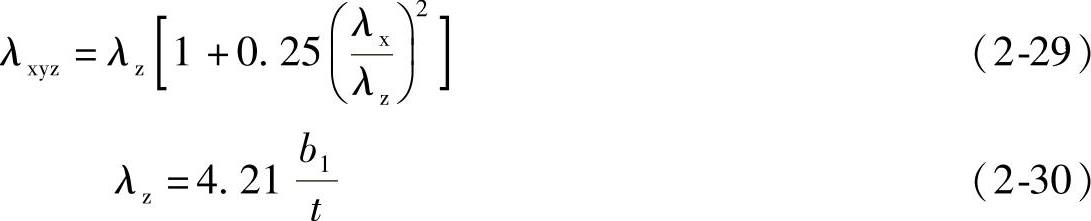
式中 x轴为角钢的主轴,b1为角钢长肢宽度。
4)格构式轴心受压构件对实轴长细比应按3)计算,对虚轴(图2-7a的x轴和图2-7b、c的x轴和y轴)应取换算长细比。换算长细比应按下列公式计算:
① 双肢组合构件(图2-7a)
当缀件为缀板时:

当缀件为缀条时:
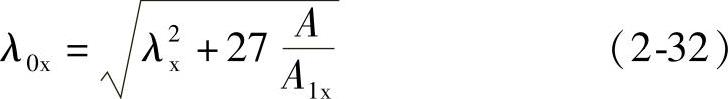
式中 λx——整个构件对x轴的长细比;
λ1——分肢对最小刚度轴1-1的长细比,其计算长度取为:焊接时,为相邻两缀板的净距离;螺栓连接时,为相邻两缀板边缘螺栓的距离;
A1x——构件截面中垂直于x轴的各斜缀条毛截面面积之和。
 (https://www.xing528.com)
(https://www.xing528.com)
图2-6 不等边角钢
② 四肢组合构件(图2-7b)
当缀件为缀板时:

当缀件为缀条时:

式中 λy——整个构件对y轴的长细比;
A1y——构件截面中垂直于y轴的各斜缀条毛截面面积之和。
③ 缀件为缀条的三肢组合构件(图2-7c)
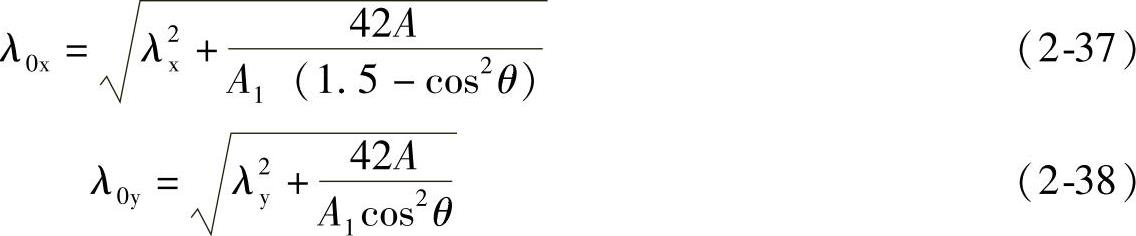
式中 A1——构件截面中各斜缀条毛截面面积之和;
θ——构件截面内缀条所在平面与x轴的夹角。
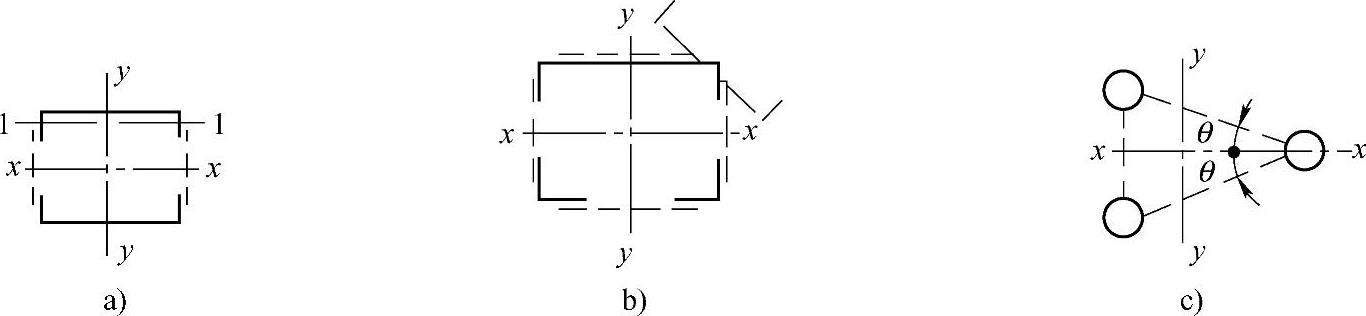
图2-7 格构式组合构件截面
a)双肢组合构件 b)四肢组合构件 c)缀件为缀条的三肢组合构件
5)两端铰支的梭形圆管或方管状截面轴压构件(图2-8)的稳定性应按式(2-8)计算。计算时A取端截面的截面面积A1,稳定系数φ按下列换算长细比确定:

式中 i1——端截面回转半径;
l0——构件计算长度,按下式计算:
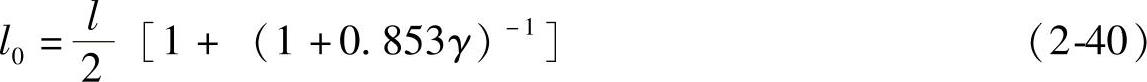
γ——构件楔率,按下式计算:
γ=(d2-d1)/d1或(b2-b1)/b1 (2-41)
d2、b2——中央截面外径(圆管),边长(方管);
d1、b1——端截面外径(圆管),边长(方管)。
6)两端铰支的多肢钢管梭形格构柱应按式(2-8)计算整体稳定。稳定系数4依据b类截面按下列换算长细比确定:

式中 n——钢管分肢数;
As——单根分肢的截面面积;
Ncr——特征值屈曲荷载,按下列公式计算:
Ncr=min(Ncr,s,Ncr,a) (2-43)
Ncr,s、Ncr,a——分别为对称屈曲模态与反对称屈曲模态对应的特征值屈曲荷载,应按下列方法计算。
① Ncr,s按下列公式计算:
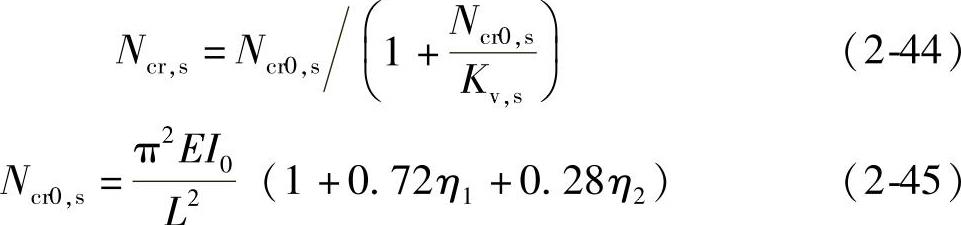
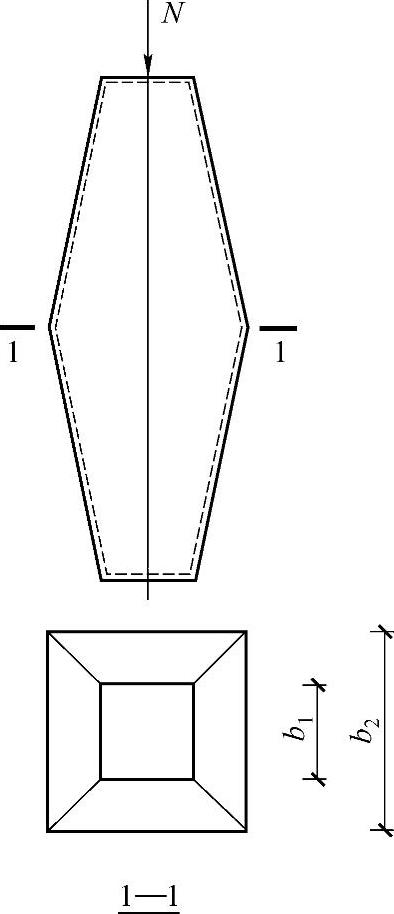
图2-8 梭形管状轴压构件
② Ncr,a按下列公式计算:
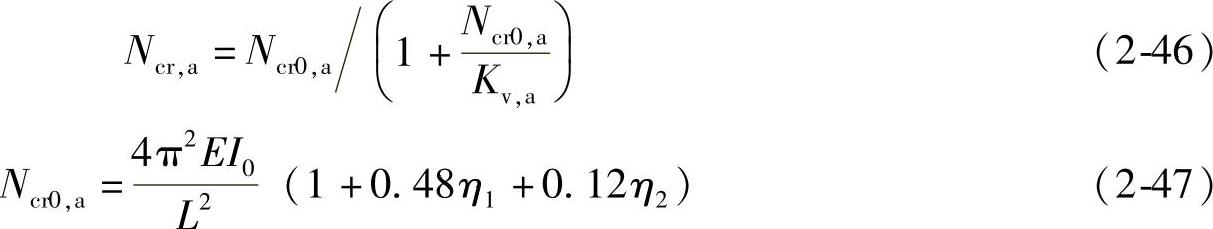
式中 Kv,s、Kv,a——分别为对称屈曲与反对称屈曲对应的截面抗剪刚度,应按下列公式计算:
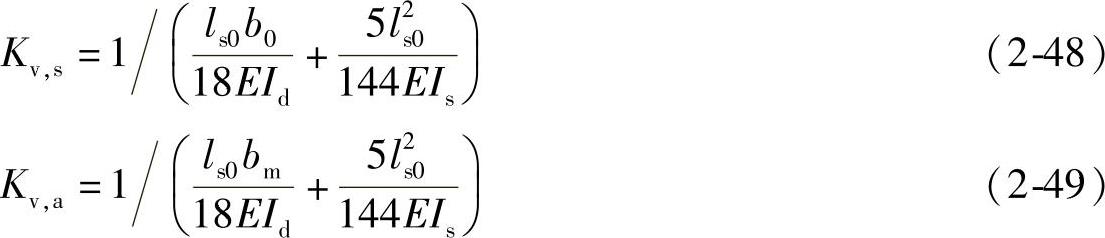
ls0——梭形柱节间高度;
Id、Is——横缀杆和弦杆的惯性矩;
E——材料的弹性模量;
η1、η2——与截面惯性矩有关的计算系数,三肢时按下列公式计算:
η1=(4Im-I1-3I0)/I0 (2-50)
η2=2(I0+I1-2Im)/I0 (2-51)
I0、Im、I1——分别为钢管梭形格构柱柱端(小头)、柱在1/4跨处以及跨中(大头)对应的惯性矩(图2-9),应按下列公式计算:
I0=3Is+0.5b20As (2-52)
Im=3Is+0.5b2mAs (2-53)
I1=3Is+0.5b21As (2-54)
b0、bm、b1——分别为梭形柱柱头、1/4跨截面和跨中截面的边长;
As——单个分肢的截面面积。
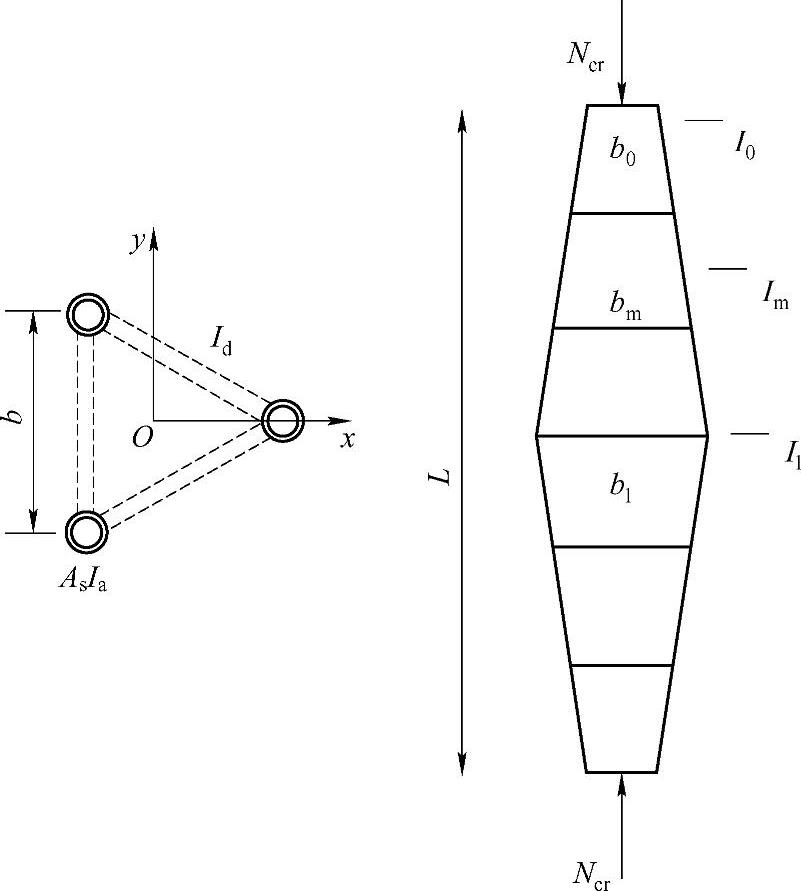
图2-9 钢管梭形格构柱
③ 钢管梭形格构柱的跨中截面应设置横隔。横隔可采用水平放置的钢板且与周边缀管焊接,或采用水平放置的钢管并使跨中截面成为稳定截面。
7)确定桁架弦杆和单系腹杆(用节点板与弦杆连接)的长细比时,其计算长度l0应按表2-21采用,采用相贯焊接连接的钢管桁架,其构件计算长度系数可按表2-22取值。
表2-21 桁架弦杆和单系腹杆的计算长度l0

注:1.l为构件的几何长度(节点中心间距离);l1为桁架弦杆侧向支承点之间的距离。
2.斜平面系指与桁架平面斜交的平面,适用于构件截面两主轴均不在桁架平面内的单角钢腹杆和双角钢十字形截面腹杆。
3.除钢管结构外,无节点板的腹杆计算长度在任意平面内均取其几何长度。
表2-22 钢管桁架构件计算长度系数

注:1.l1为平面外无支撑长度;l是杆件的节间长度。
2.对端部缩头或压扁的圆管腹杆,其计算长度取1.0l。
8)当桁架弦杆侧向支承点之间的距离为节间长度的2倍(图2-10)且两节间的弦杆轴心压力不相同时,则该弦杆在桁架平面外的计算长度,应按下式确定(但不应小于0.5l1):

式中 N1——较大的压力,计算时取正值;
N2——较小的压力或拉力,计算时压力取正值,拉力取负值。
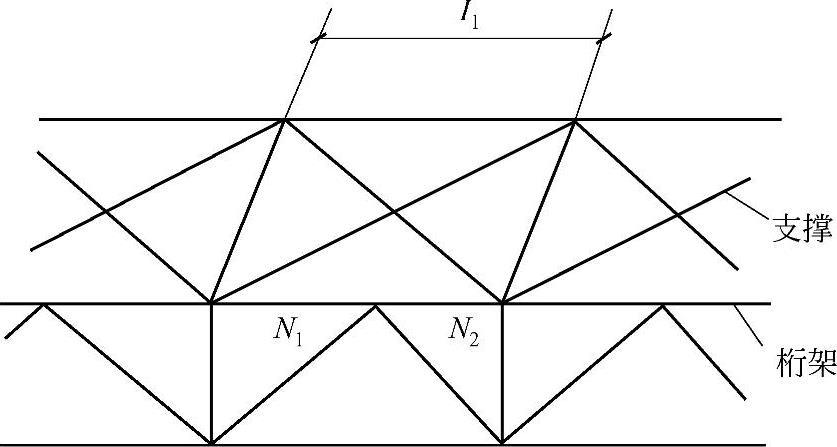
图2-10 弦杆轴心压力在侧向支承点间有变化的桁架简图
桁架再分腹杆体系的受压主斜杆及K型腹杆体系的竖杆等,在桁架平面外的计算长度也应按式(2-55)确定(受拉主斜杆仍取l1);在桁架平面内的计算长度则取节点中心间距离。
9)轴压构件的长细比不宜超过表2-23规定的容许值,受拉构件的长细比不宜超过表2-24规定的容许值。
表2-23 受压构件的容许长细比

注:1.当杆件内力设计值不大于承载能力的50%时,容许长细比值可取200。
2.计算单角钢受压构件的长细比时,应采用角钢的最小回转半径,但计算在交叉点相互连接的交叉杆件平面外的长细比时,可采用与角钢肢边平行轴的回转半径。
3.跨度等于或大于60m的桁架,其受压弦杆、端压杆和直接承受动力荷载的受压腹杆的长细比不宜大于120。
4.验算容许长细比时,可不考虑扭转效应。
表2-24 受拉构件的容许长细比
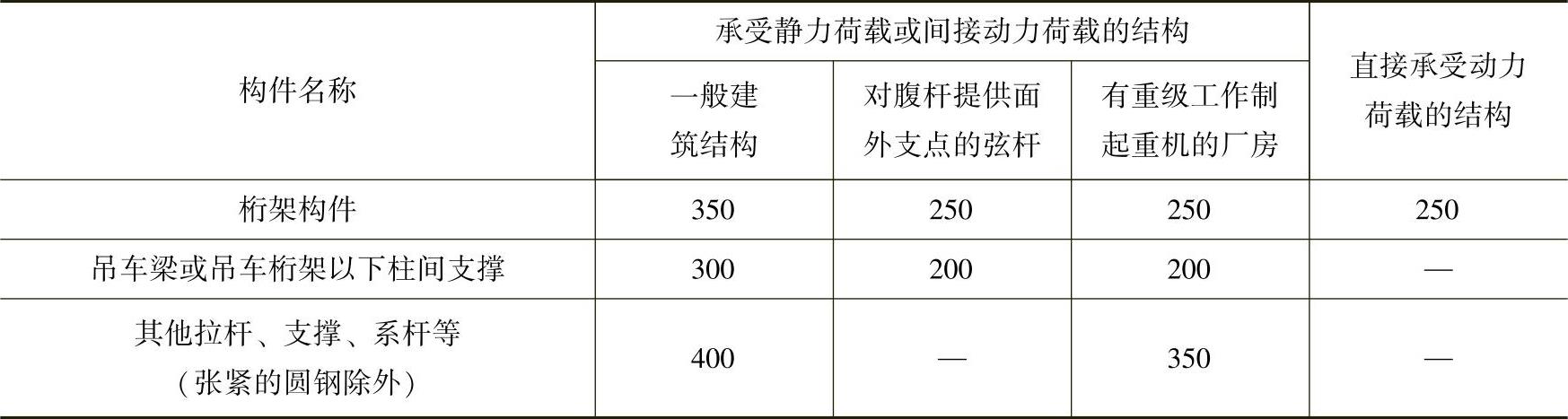
注:1.除对腹杆提供面外支点的弦杆外,承受静力荷载的结构受拉构件,可仅计算竖向平面内的长细比。
2.在直接或间接承受动力荷载的结构中,计算单角钢受压构件的长细比时,应采用角钢的最小回转半径,但计算在交叉点相互连接的交叉杆件平面外的长细比时,可采用与角钢肢边平行轴的回转半径。
3.中、重级工作制吊车桁架下弦杆的长细比不宜超过200。
4.在设有夹钳或刚性料耙等硬钩起重机的厂房中,支撑的长细比不宜超过300。
5.受拉构件在永久荷载与风荷载组合作用下受压时,其长细比不宜超过250。
6.跨度等于或大于60m的桁架,其受拉弦杆和腹杆的长细比不宜超过300(承受静力荷载或间接承受动力荷载)或250(直接承受动力荷载)。
7.柱间支撑按拉杆设计时,竖向荷载作用下柱子的轴力应按无支撑时考虑。
10)桁架受压弦杆的横向支撑系统中系杆和支承斜杆应能承受下式给出的节点支撑力(图2-11):

式中 ∑N——被撑各桁架受压弦杆最大压力之和;
m——纵向系杆道数(支撑系统节间数减去1);
n——支撑系统所撑桁架数。
11)塔架主杆与主斜杆之间的辅助杆(图2-12)应能承受下列公式给出的节点支撑力:
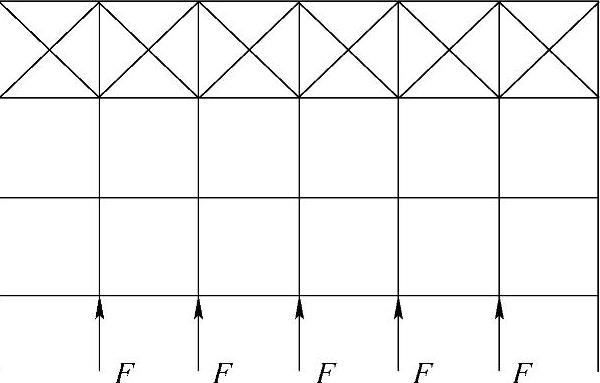
图2-11 桁架受压弦杆横向支撑系统的节点支撑
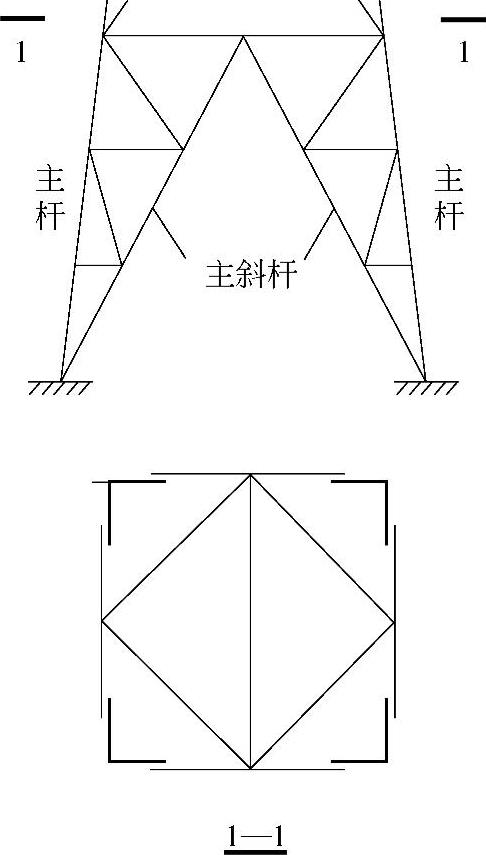
图2-12 塔架下端示意图
当节间数不超过4时
F=N/80 (2-57)
当节间数大于4时
F=N/100 (2-58)
式中 N——主杆压力设计值。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




