落差法：水位变动影响下的整编方法

对于受变动回水影响的测站可以用落差法进行整编，其基本关系式为

图3.50　某水文站水位后移法实例

对于受洪水涨落影响的测站，只要比降与落差的关系较好，也可以用落差法进行整编。因为从洪水涨落影响下的流量公式中知：

其中：为洪水波附加比降，为洪水波的水面比降，则上式为，当比降与落差关系较好，并将“1/2”用β′代替时，则

此时的β′除含有β值的含义外，还有因洪水波传播引起的比降因素，即β′=β+Δβ。当落差与比降关系好时，Δβ≈0。式（3.23）可以改写为

1.定落差法

该法适用于断面比较均匀，河底比较平坦，在不受回水影响时水面比降接近河底坡度的测站。同水位下，不同的落差与流量之间关系符合式（3.24），定线时，一般先选定实测落差的较大者作为定落差ΔZc，与定落差相应的流量，称为定落差流量Qc，它和水位呈单值关系。已知实测流量Qm、落差ΔZm及相应水位，未知量为ΔZc、Qc、落差指数β，要求解它们必须建立有关方程组进行求解。定落差法所用到的方程式为

具体计算时采用试算法求解，步骤如下。

（1）点绘Z-Qm关系点，并注上各点相应落差ΔZm；选ΔZm中较大者作为定落差ΔZc。

（2）计算与Qm同水位的定落差流量。

（3）点绘Z-Qc关系点，并定出关系线Z-Qc。

（4）在Z-Qc关系线上，由实测水位Z查读相应流量Q c。

（5）计算同一水位下的（Qm/Qc）和（ΔZm/ΔZc），点绘经过点（1，1）的关系曲线（Qm/Qc）-（ΔZm/ΔZ c）。

（6）检验：由实测水位Z相应的ΔZm和已知的ΔZc计算出ΔZm/ΔZc，并在曲线上查得校正的［Qm/Qc］；计算Q′c=Qm/［Qm/Qc］；在原图上点绘Z-Q′c关系点，这些点据称为定落差点，并检验这些点子是否密集在原定曲线两侧，如果密集，则定线完毕，这时所定Z-Qc和（Qm/Qc）-（ΔZm/ΔZ c）曲线为所求；如果不密集，则修改Z-Qc关系线。

（7）推流：已知Z、ΔZc、ΔZm及所定的Z-Qc、（Qm/Qc）-（ΔZm/ΔZc）两关系曲线，由Z在Z-Qc曲线上查出Q c，计算（ΔZm/ΔZ c）并在（Qm/Qc）-（ΔZm/ΔZc）关系曲线查出对应的（Qm/Qc）值，则Z所相应的流量，如图3.51所示。

图3.51　定落差法水位流量关系图

2.等落差法

本法的基本假定是：断面稳定，用上下落差水尺计算的比降能代表基本水尺处的水面比降。此时，流量可表示为水位落差的函数Q=f（Z，ΔZ）。

当落差ΔZ不变。Q是Z的单值函数，此时定出一条单一的稳定曲线；当Z不变时，Q是落差的函数，同水位下，流量将随落差的不同而不同。本法特点是：以落差为参数，绘制各种落差下的水位流量关系曲线，形成曲线簇。要求流量测点较多，且能分布于各级水位和各种落差值的情况下，才能定出比较合理的曲线簇。(www.xing528.com)

定线推流方法如下。

（1）在水位流量关系图上，点绘关系点，并将落差值注在测点旁边。

（2）依据测点落差值相近，高低水控制较好的测点，绘制已确定的等落差下的流量相关曲线，如图3.52所示。

（3）曲线簇的调正，即用式（3.25）

两相邻曲线的落差ΔZ 1、ΔZ 2为已知，其比值的β次方亦为定值。因此，在各级水位的同水位下，Q 1/Q 2的比值应为定值，若有变化，表示不符合式（3.25），应进行调整曲线，使之基本符合为止。

图3.52　等落差水位流量关系曲线

（4）插补曲线：有时确定的落差值的测点太少，无法据以定线，此时可根据式（3.25）的特性，插补一些测点，从而确定和延长某些等落差下的相关曲线。方法是将式（3.25）取对数，求出β。

整理得

如图3.53所示，已知ΔZ 1、ΔZ 4两条等值线相关曲线已定出，欲插ΔZ 2、ΔZ 3的曲线，可用已知的ΔZ 1、ΔZ 4两条曲线反求出β值，再按分水位级算出各级水位下的Q 2、Q 3，从而可定出等落差值ΔZ 2、ΔZ 3下的水位流量关系曲线，如图3.53所示。

图3.53　等落差水位流量关系曲线插补

（5）推流：以基本水尺处的水位及其落差值，在曲线簇中相应的落差曲线上直接查读流量，无此落差值的曲线时，在两已知落差曲线内插得出。

3.落差指数法

落差指数法以落差法为基础，通过优选落差指数β，并建立水位与流量同落差β次方之比的关系曲线来整编流量。该法适用于断面基本稳定，受变动回水或变动回水及洪水涨落综合影响的测站。

将落差法基本公式变换为：，在同水位下，Q/（ΔZ）β为一常数，即Q/（ΔZ）β是水位的单值函数，Q/（ΔZ）β=f（Z）为单一关系。落差指数β必须通过试算，根据方差或标准差最小的原则优选。在率定水位Z与Q/（ΔZ）β关系（定线）时，已知：实测流量Qm及相应水位Z m和落差ΔZm；具体操作时，可以通过建立落差指数β和ZQm/（ΔZm）β关系曲线求解。

图3.54　某水文站落差指数与标准差关系图

首先，假定初始值β1，根据实测流量Qm及相应落差ΔZ，计算qm=Qm/（ΔZ）β1值，点绘Zm-qm关系线或选配Zm-qm关系方程，由各点与关系线的离差求出其相应的标准差S 1（或方差），再假定一个β2（＞β1）。重复上述步骤，又得到标准差S 2。再假定几个β值，就得到一系列数据（β1，S 1）、（β2，S 2）、…，绘制β-S关系线，如图3.54所示，以标准差最小为目标，即可寻得最优的β值。将优选的S与规范规定的水力因素型方法定线标准差进行比较，若符合规定标准，则β值和Z-qm关系曲线即为所求，如图3.55所示。

推流时，根据优选的β值，计算落差ΔZ、ΔZβ值，用本站实测水位在Z-qm关系曲线上查得q m值，将它与相应时间的ΔZβ值相乘，即可求得Qm值。

图3.55　落差指数法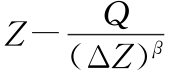关系曲线