铁路混凝土桥梁简支梁桥剪力键分析

缩尺铁路简支梁桥剪力键的研究通过数值分析与试验验证来进行。振动台试验中，剪力键的水平承载能力通过抗剪螺栓的数量来控制。单个支座的单侧剪力键强度试验结果见表7.6-1，下文为数值模拟计算结果。

表7.6-1　剪力键强度试验结果

数值模拟剪断力通过不断增加水平刚度（模拟试验中增加剪力螺栓数量）来确定，取值原则为7度地震作用下保证剪力键不被剪断或者少量被剪断，8度地震作用下全被剪断。分别对8 m、25 m墩高模型进行纵桥向和横桥向分析。

7.6.1.1　8 m墩高纵桥向

试验结果表明，在7度地震作用下，剪力键未被剪断，承受最大的纵向剪力为8 kN，小于11 kN。当8度地震激励下，剪力键均在受到11 kN水平力时被剪断。固定支座的剪力键在0.9 s时被剪断，滑动支座的剪力键在1.3 s时被剪断。如图7.6-1所示，实线表示固定支座附近的剪力键，虚线表示滑动支座附近的剪力键。其原因是固定支座的刚度较大，所以首先受到的水平剪力较大。随着固定支座的剪力键被剪断，主梁相对于墩顶的位移变大，致使滑动支座在纵向滑动时撞到限位块（本试验模型的滑动距离为±5 mm），因此剪力键被撞断。

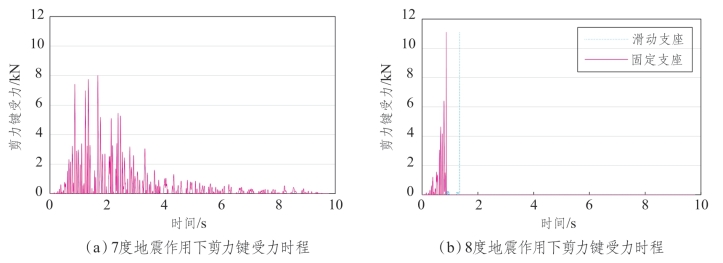
图7.6-1　缩尺铁路梁桥剪力键纵向受力时程

从图7.6-2可以发现，由于剪力键一开始未被剪断，固定支座下部的双曲面摩擦摆部分的位移几乎为0。在0.9 s时，纵向剪力键被剪断，支座开始摆动，起到隔震效果。

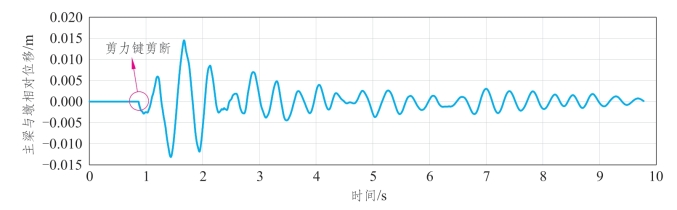
图7.6-2　缩尺铁路梁桥支座纵向位移时程

如图7.6-3所示，实线表示隔震工况，虚线表示未隔震的工况。可以发现隔震工况有4个用圆圈住的峰值。“固定1”表示0.9 s时刻固定支座的单侧剪力键被剪断时混凝土应变的峰值；“固定2”表示0.9 s时刻固定支座的另一侧剪力键被剪断时混凝土应变的峰值；“滑动1”表示1.2 s时刻滑动支座的单侧剪力键被剪断时混凝土应变的峰值；“滑动2”表示1.3 s时刻滑动支座的另一侧剪力键被剪断时混凝土应变的峰值。隔震工况下压应变峰值为1.17×10－4，未隔震工况下压应变峰值为1.80×10－4，隔震效率为35%。隔震工况下拉应变峰值为1.01×10－4，未隔震工况下拉应变峰值为1.65×10－4，隔震效率为39%。

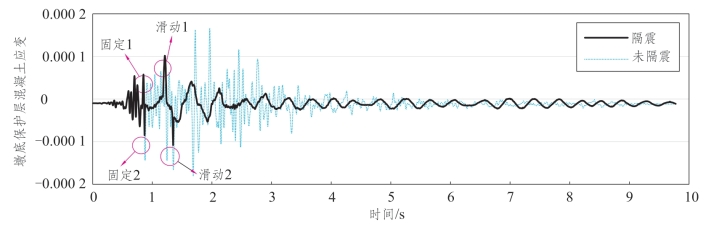
图7.6-3　缩尺铁路梁桥墩底纵向保护层混凝土应变时程

7.6.1.2　8 m墩高横桥向

试验结果表明，在7度地震作用下，剪力键未被剪断，承受最大的横向剪力为4.4 kN，小于6 kN。在8度地震作用下，剪力键均在受到5.6 kN水平力时被剪断。如图7.6-4所示，图中所示的剪力键在1.4 s时被剪断。剪力键设定剪断力为6 kN，但是结果却未达到6 kN。这是由于数值模拟输出数据的时间间隔为0.002 39 s，因此剪断力在输出结果中并未达到6 kN。

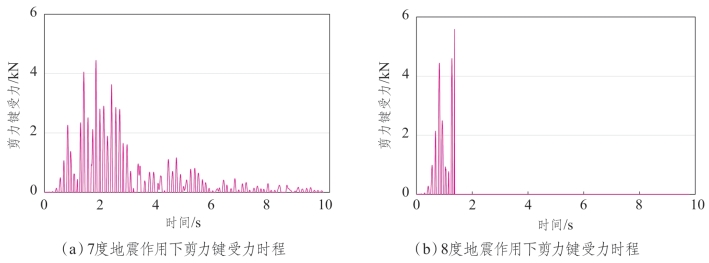
图7.6-4　缩尺铁路梁桥剪力键横向受力时程

从图7.6-5可以发现，由于剪力键一开始未被剪断，固定支座下部的双曲面摩擦摆部分的位移几乎为0。在1.4 s时，横向剪力键被剪断，支座开始摆动，起到隔震效果。

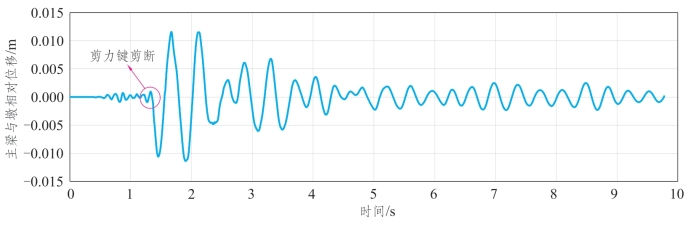
图7.6-5　缩尺铁路梁桥支座横向位移时程

如图7.6-6所示，实线表示隔震工况，虚线表示未隔震的工况。可以发现隔震工况有2个用圆圈住的峰值。“左侧剪力键”表示1.4 s时刻支座的左侧剪力键被剪断时混凝土应变的峰值；“右侧剪力键”表示1.6 s时刻支座的右侧剪力键被剪断时混凝土应变的峰值。隔震工况下压应变峰值为1.78×10－4，未隔震工况下压应变峰值为3.28×10－4，隔震效率为46%。隔震工况下拉应变峰值为1.97×10－4，未隔震工况下拉应变峰值为6.08×10－4，隔震效率为66%。

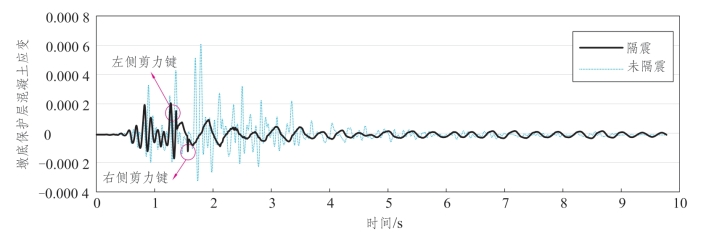
图7.6-6　缩尺铁路梁桥墩底横向保护层混凝土应变时程

7.6.1.3　25 m墩高纵桥向(www.xing528.com)

如图7.6-7所示，实线表示固定支座附近的剪力键，虚线表示滑动支座附近的剪力键。试验结果表明，在7度地震作用下，剪力键未被剪断，承受最大的纵向剪力为3.9 kN，小于7 kN。在8度地震作用下，剪力键均在受到7 kN水平力时被剪断。固定支座的剪力键在1.4 s时被剪断，滑动支座的剪力键在2.0 s时被剪断。其原因是固定支座的刚度较大，所以首先受到的水平剪力较大。随着固定支座的剪力键被剪断，主梁相对于墩顶的位移变大，致使滑动支座在纵向滑动时撞到限位块（本试验模型的滑动距离为±5 mm），因此剪力键被撞断。

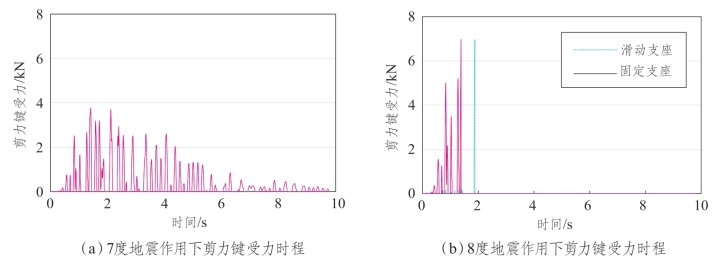
图7.6-7　缩尺铁路梁桥剪力键纵向受力时程

从图7.6-8可以发现，由于剪力键一开始未被剪断，固定支座下部的双曲面摩擦摆部分的位移几乎为0。在1.4 s时，纵向剪力键被剪断，支座开始摆动，起到隔震效果。

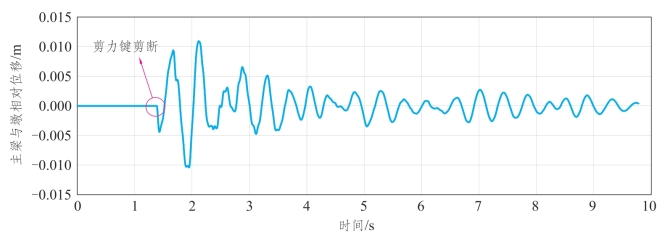
图7.6-8　缩尺铁路梁桥支座纵向位移时程

如图7.6-9所示，实线表示隔震工况，虚线表示未隔震的工况。隔震工况下压应变峰值为8.77×10－5，未隔震工况下压应变峰值为9.32×10－5，隔震效率为6%。隔震工况下拉应变峰值为3.15×10－5，未隔震工况下拉应变峰值为1.51×10－4，隔震效率为80%。

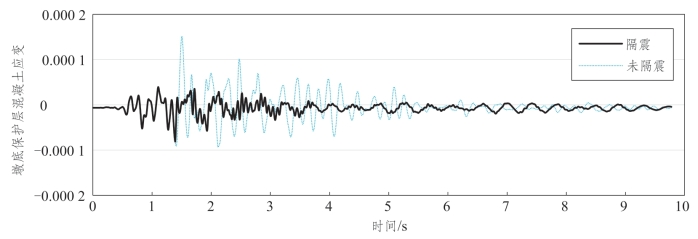
图7.6-9　缩尺铁路梁桥墩底纵向保护层混凝土应变时程

7.6.1.4　25 m墩高横桥向

试验结果表明，在7度地震作用下，剪力键未被剪断，承受最大的纵向剪力为2.7 kN，小于5 kN。在8度地震作用下，剪力键均在受到5 kN水平力时被剪断。剪力键在1.7 s时被剪断，如图7.6-10所示。

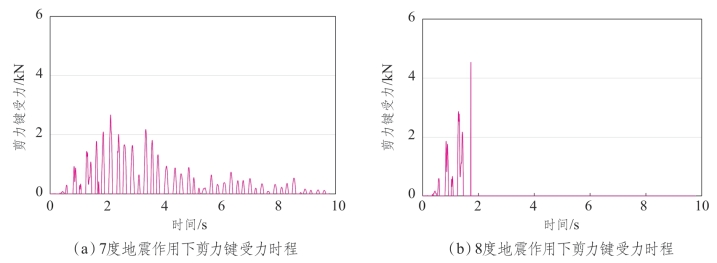
图7.6-10　缩尺铁路梁桥剪力键横向受力时程

从图7.6-11可以发现，由于剪力键一开始未被剪断，固定支座下部的双曲面摩擦摆部分的位移几乎为0。1.5 s时，横向剪力键被剪断，支座开始摆动，起到隔震效果。

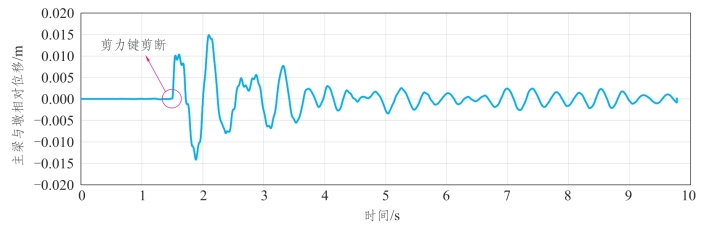
图7.6-11　缩尺铁路梁桥支座横向位移时程

如图7.6-12所示，实线表示隔震工况，虚线表示未隔震的工况。可以发现隔震工况有2个用圆圈住的峰值。“左侧剪力键”表示1.5 s时刻支座的左侧剪力键被剪断时混凝土应变的峰值；“右侧剪力键”表示1.6 s时刻支座的右侧剪力键被剪断时混凝土应变的峰值。隔震工况下压应变峰值为1.50×10－4，未隔震工况下压应变峰值为1.77×10－4，隔震效率为15%。隔震工况下拉应变峰值为8.67×10－5，未隔震工况下拉应变峰值为1.72×10－4，隔震效率为50%。

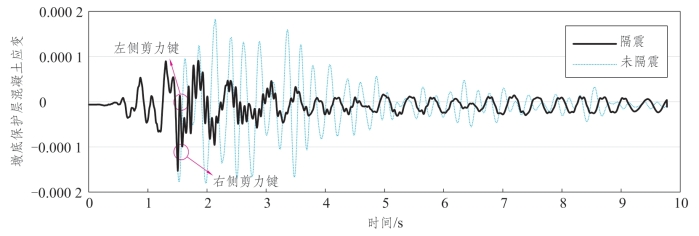
图7.6-12　缩尺铁路梁桥墩底横向保护层混凝土应变时程

根据上文数值模拟结果，总结见表7.6-2，试验值与数值计算结果误差控制在20%以内，有限元模型建立合理。

表7.6-2　剪力键剪断力试验值与理论值比较

数值模拟缩尺模型的剪断力通过不断增加水平刚度来确定，取值原则为7度地震作用下保证剪力键不被剪断或者少量被剪断，8度地震作用下剪力键全部被剪断或少量没有被剪断。8 m墩高缩尺模型纵桥向和横桥向剪断力分别是11 kN和6 kN，25 m墩高缩尺模型纵桥向和横桥向剪断力分别是7 kN和5 kN。振动台试验值与理论值之间的误差控制在20%以内，验证了缩尺有限元模型剪力键的合理性。