约束箍筋用量的理论与试验研究成果

以曲率延性系数为抗震指标的约束箍筋用量研究受到众多学者认可，且研究成果众多。国内外学者在大量试验基础上，基于不同的考量，提出了混凝土桥墩不同曲率延性水平的塑性铰区约束箍筋用量计算公式，总结如表5.4-14所示。

表5.4-14　约束箍筋用量计算公式（曲率）

续表

其中：k是与曲率延性系数相关的系数，ωwd=，α为箍筋有效约束系数，η为轴压比，λcv=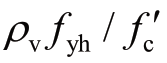，Ag、Ac分别为全截面面积和核心混凝土面积，m=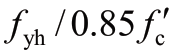，φ为强度安全系数，“圆形”表示圆形截面，“矩形”表示矩形截面，以下各表中符号的意义相同。

上述公式的最大特点是以曲率延性系数作为性能指标，具有形式简单、便于工程实际应用等诸多优点。但部分学者认为以位移延性系数作为延性指标更能直接反映桥墩的抗震水平，针对不同地震危险性给出了框架柱约束箍筋用量的设计方法，总结如表5.4-15所示。

表5.4-15　约束箍筋用量计算公式（位移）

其中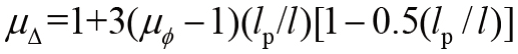：，DRmax，p=（4-4.5η）/100，cmax，p=0.2+0.3ηk，μΔ　=（1+1.5η）×DRlim。

尽管以上公式得到诸多认可，但仍有学者认为桥墩极限位移角具有定义简单且可以直接测量等优点，其与曲率延性、位移延性系数有很好的对应关系，进而相继提出了以极限位移角作为量化指标的约束箍筋用量计算公式，总结如表5.4-16所示。

表5.4-16　约束箍筋用量计算公式（转角）

注：m=fyh/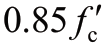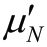，=N/[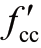（Acor-As）+fyAs]。

上述基于曲率、位移及转角的三类公式存在以下特点：

（1）上述公式给出了箍筋用量最小值，无法准确给出实际桥墩的配箍定量；

（2）对于给定箍筋用量的既有桥墩，无法通过箍筋用量直接预测墩的位移延性；(www.xing528.com)

（3）既有公式没有考虑剪跨比及空心截面形式的影响。

为此，基于14个空心墩及7个实体墩（部分设计参数如表5.4-17所示）拟静力试验研究配箍率、配筋率、剪跨比及截面形式对位移延性系数的影响，并结合文献数据，对于空心、实体桥墩分别给出位移延性系数关于轴压比、剪跨比、纵筋及混凝土强度、配筋率及配箍率的表达式。各构件轴压比统一为0.05，采用C40混凝土，纵向钢筋HRB400，箍筋及拉筋HRB335。基于实测滞回曲线得到骨架曲线，确定屈服点；以试件侧向承载能力下降到最大侧向承载能力的85%时定义为其极限状态。根据设计参数分组情况，将两种墩型位移延性、剪跨比、配筋率的变化情况分别绘于图5.4-11中。其中，空心墩和实体墩位移延性的对比结果如图5.4-11（a）所示；图5.4-11（b）给出相同截面形式、配筋率和箍筋率情况下位移延性随剪跨比的变化趋势；图5.4-11（c）、（d）分别给出位移延性随配箍率、配筋率的变化趋势。

表5.4-17　拟静力试验桥墩模型设计参数

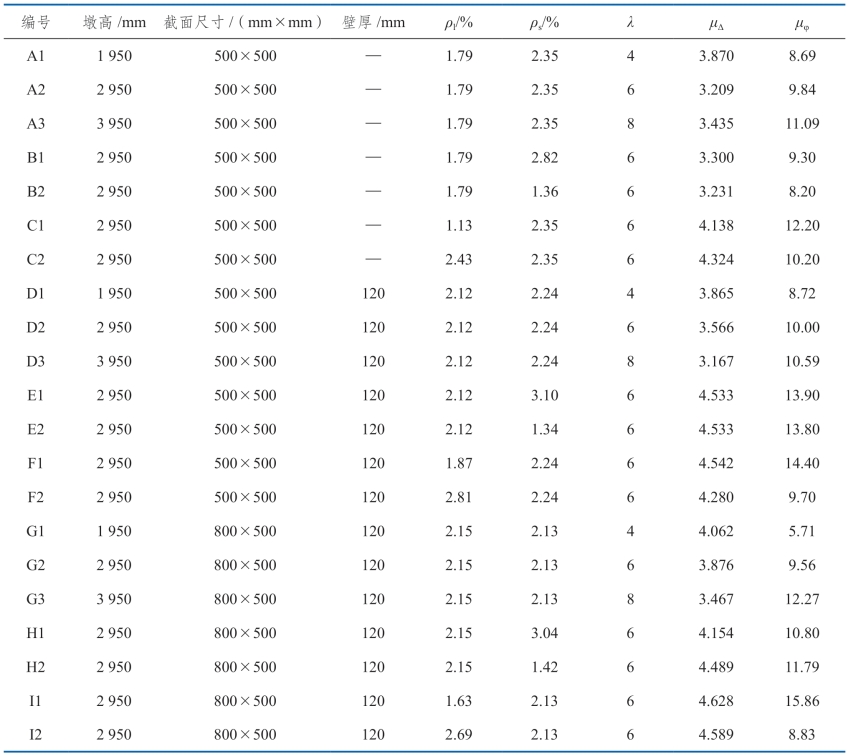
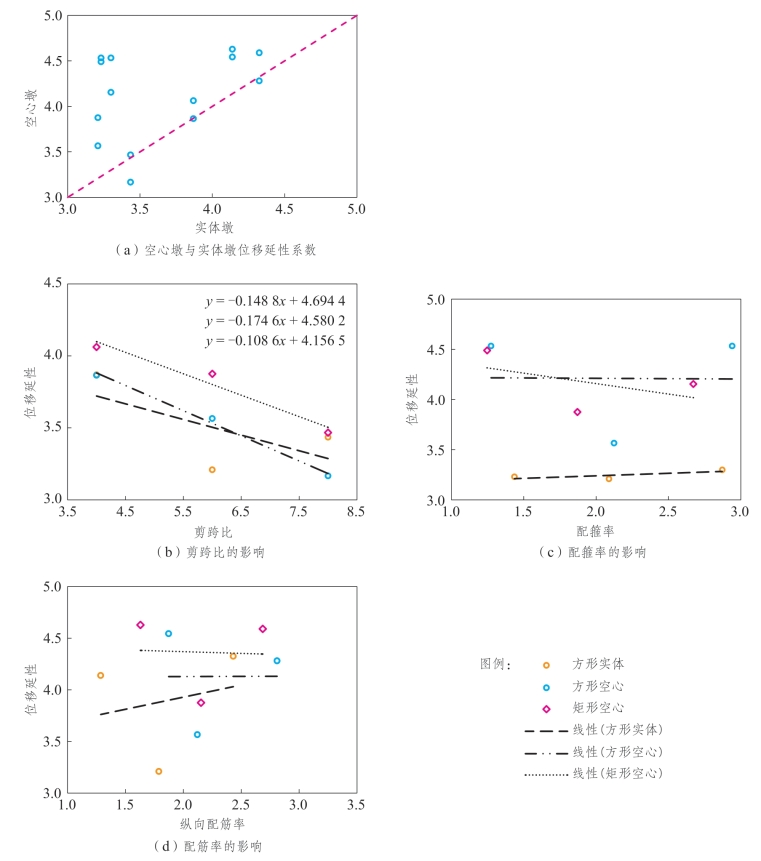
图5.4-11　位移延性的试验结果

上述试验结果表明：剪跨比、配箍率及配筋率对矩形实体、空心墩的位移延性系数均有一定影响；相对具有相同截面外尺寸的实体墩，空心墩延性更好，如图5.4-11（a）所示；相同设计参数的方形实体、方形空心及矩形空心墩的位移延性均随剪跨比增大而减小，如图5.4-11（b）所示；箍筋对实体墩位移延性的提高大于空心墩，如图5.4-11（c）所示；配筋率对空心墩、实体墩位移延性的影响程度有一定差别，如图5.4-11（d）所示。

由此，得到约束箍筋用量的通用计算公式：

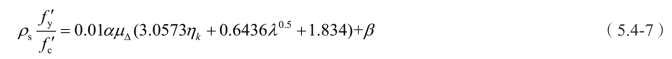
式中，α、β、λ取值参见表5.4-18。

表5.4-18　不同类型桥墩参数值

回归公式计算结果与已有公式的比较，见图5.4-12。

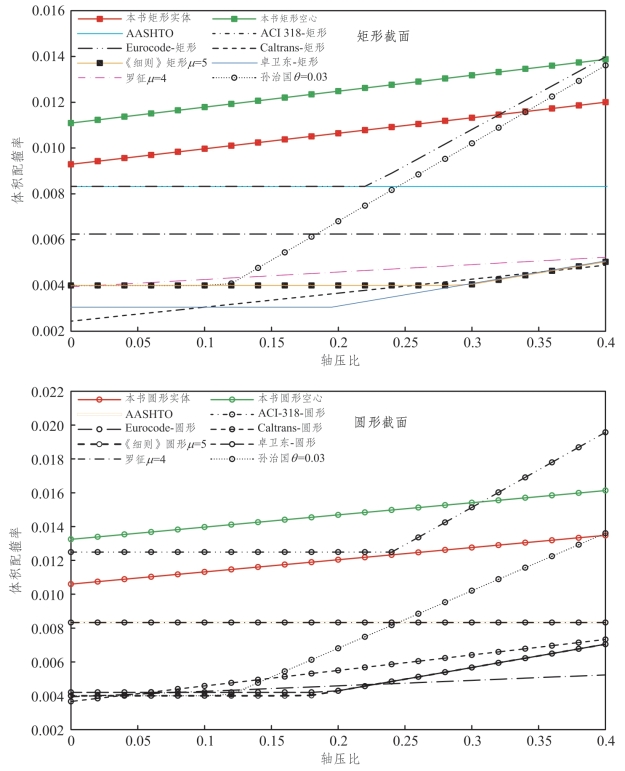
图5.4-12　回归公式计算结果与已有公式比较

可见：既有公式计算结果普遍小于实际配箍率，除个别试件外，回归公式计算结果略大于实际配箍率。对于圆形实心墩，与计算效果较好的Eurocode 8相比，回归公式结果与实际配箍率更为接近。对于矩形空心墩，既有公式普遍未考虑剪跨比及配筋率的影响，因此试验空心墩配箍率的计算结果基本不变，其中与较接近设计值的AASHTO、Eurocode 8相比，回归公式计算值大部分相对保守。综上所述，回归公式计算值与实际设计值吻合程度相对较好；较现有公式，本书算法更适用于估算各类桥墩在不同轴压比、剪跨比及位移比下的约束箍筋设计用量。