铁路混凝土桥梁抗震设计：桥墩有效刚度的控制因素和参数模型

在地震荷载作用下，钢筋混凝土桥墩通常处于带裂缝工作状态，使得桥梁结构的抗弯刚度下降。在桥梁抗震验算中，桥墩整体有效刚度的取值对桥梁构件及桥梁整体的响应需求计算和延性能力估计都有较大的影响。

影响桥墩有效刚度的因素主要有：纵筋率、纵筋直径、轴压比、墩高、剪跨比（长细比）、配箍率、纵筋屈服强度以及混凝土抗压强度等。配筋情况、几何尺寸、材料性能及截面受力特性和内力状态有关。

由此可见，轴压比、剪跨比是桥墩有效刚度的控制因素。剪跨比对刚度的影响如图5.4-5所示。

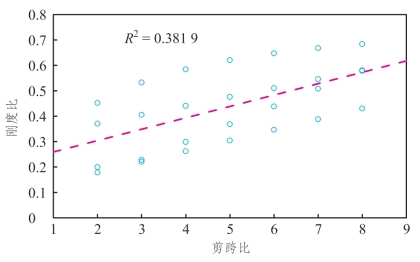
图5.4-5　剪跨比的影响

基于上述分析，给出有效刚度关于轴压比、剪跨比的待定参数模型：

式中，f（μ）是轴压比μ的函数，f（λ）是剪跨比λ的函数，β为待定参数。

采用全部桥墩中22个实体墩的拟静力试验数据对式（5.4-5）进行待定参数标定，通过多元回归得到实体墩有效刚度比的计算公式如下：

根据上述研究思路，基于全部桥墩中的28个空心墩试验结果，通过多元非线性回归得到空心墩有效刚度比的计算公式如下：

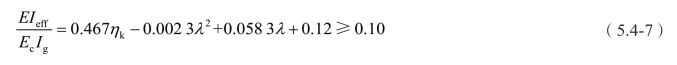
以下分别将回归公式（5.4-6）、（5.4-7）称为公式Ⅰ、公式Ⅱ。为了检验公式Ⅰ、公式Ⅱ的合理性及有效性，作者采用剩余67个桥墩（其中实体墩38个、空心墩29个）的试验结果分别对回归公式进行评估，并与已有公式计算结果进行比较。

实体墩、空心墩回归公式有效刚度比计算值与试验值的比较结果如图5.4-6、表5.4-10所示。由计算与试验结果的对比分析可知，公式Ⅰ、公式Ⅱ对应的线性相关系数分别为0.921和0.821，而实体墩较空心墩的计算结果更好，公式Ⅰ、公式Ⅱ计算结果与试验值较为接近。

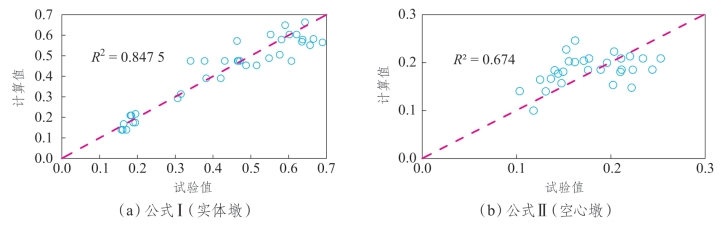
图5.4-6　有效刚度比计算值与试验值比较(www.xing528.com)

表5.4-10　有效刚度比的计算值与试验值之比的统计结果

根据《铁路工程抗震设计规范》（2009年版）的规定，钢筋首次屈服时的刚度作为桥墩有效刚度，测试有效刚度及修正系数计算结果如表5.4-11所示。

表5.4-11　测试有效刚度及修正系数

国外公式及规范公式计算结果如表5.4-12、图5.4-7、图5.4-8所示。

表5.4-12　现有公式计算效果对比

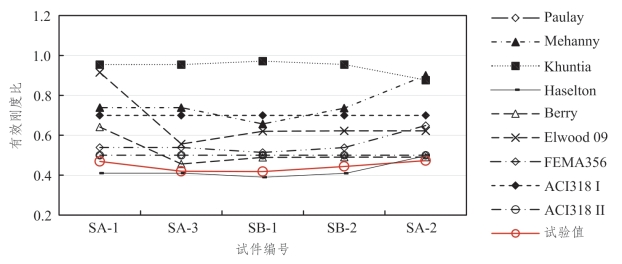
图5.4-7　有效刚度计算值与试验值（原始值）

图5.4-8　有效刚度计算公式（计算值/试验值）

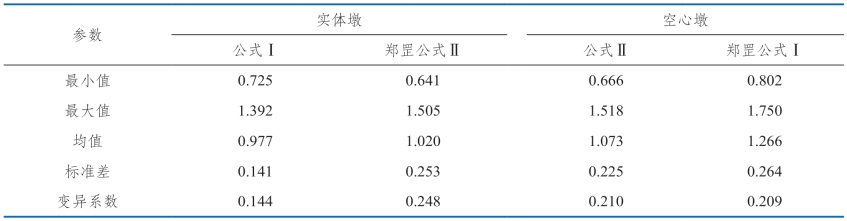
既有公式一般都是在对某种特定受力状态或几何特征的试件进行有限个试验模型研究的基础上提出来的，往往只是适用于某种特定几何条件和受力状态的构件，在使用上存在较大局限性。本次试验模型是圆端形空心混凝土桥墩，现有公式和规范计算结果与试验结果有较大差异。通过对表5.4-12、图5.4-7、图5.4-8中圆端形空心墩有效刚度估计结果对比分析，试验结果与各公式计算值变化差异较大，但总体上呈现一定规律。公式Ⅱ和郑罡公式Ⅰ计算值均较接近于试验值；与主要考虑了轴压比及剪跨比影响的郑罡公式Ⅱ相比，考虑轴压比、剪跨比、纵向配筋率、纵筋直径、纵筋抗拉强度及混凝土抗压强度等多因素综合影响的郑罡公式Ⅰ计算效果更好。综上，公式Ⅱ、郑罡公式Ⅰ对于圆端形空心墩有效刚度的估计效果相对较好。