铁路桥梁设计中的桥墩等效塑性铰长度

等效塑性铰长度的计算准确性对于桥墩抗震性能的评估至关重要，直接影响到墩顶位移计算值的大小。现有规范中等效塑性铰长度的计算公式大多是基于实体墩试验得到的，鉴于空心墩与实体墩的差异，既有等效塑性铰长度计算模型对空心墩的适用性尚有待深入研究。通过不同设计参数的铁路圆端形空心墩的拟静力试验，观测墩底塑性铰区域的破坏情况，研究轴压比和配箍率对墩顶极限位移的影响。通过现行国内外等效塑性铰长度经验计算公式与试验结果进行对比分析，探究轴压比和配箍率对空心墩等效塑性铰长度的影响，研究等效塑性铰长度计算模型对空心墩的适用性。

表5.4-7　塑性铰区长度计算公式

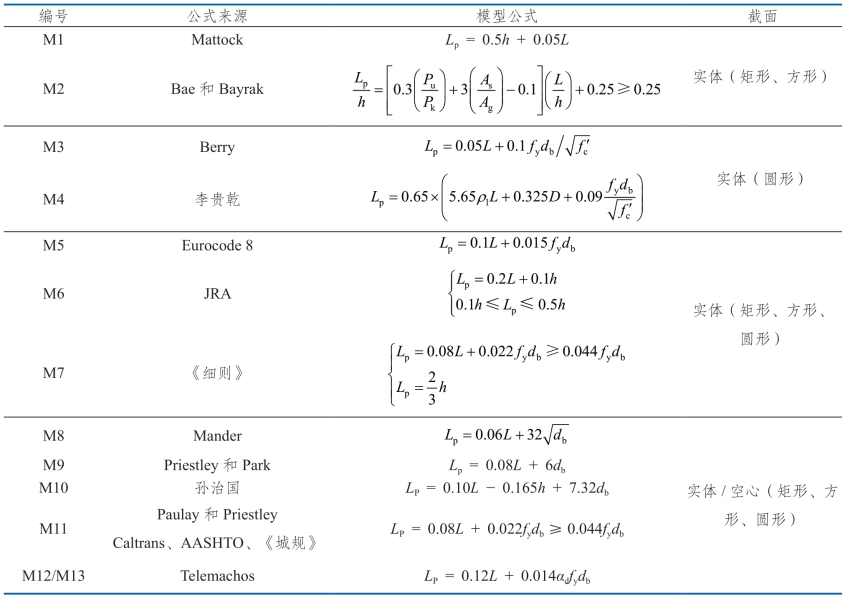
注：L为桥墩计算高度，h为截面有效高度，db为纵筋直径，fy为纵筋抗拉强度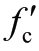，为混凝土抗压强度，Pu为构件的轴向力，Pk=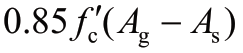+fyAs（其中As为受拉钢筋的面积，Ag为毛截面面积），ρl为纵筋率，αd考虑纵筋拔出效应时取为1（不考虑纵筋拔出效应时取为0）；Telemachos模型回归时样本中还包含了少量混凝土梁及剪力墙，M12为不考虑钢筋拔出效应的Telemachos模型，M13为考虑钢筋拔出效应的Telemachos模型。

通过对表5.4-7分析发现，现有等效塑性铰长度计算公式大多源于实体墩，这些公式能否直接适用于圆端形空心墩、现有少数空心墩计算公式的适用范围，都有待深入研究。根据所测墩身竖向位移可以计算得到各节段平均曲率，如图5.4-1所示。随着墩顶位移的不断增加，墩身各节段区域的平均曲率也随之增大。但是，墩身曲率分布与等截面实体墩存在显著差异，墩底倒角所在的区域2处平均曲率φ2明显大于区域1处平均曲率φ1。而随着截面高度的增加，在区域3处的平均曲率φ3与φ2相比急剧减小，区域4处曲率φ4略小于φ3，由此可知除区域2外墩身其余部分塑性程度相对较低。

图5.4-1　圆端形空心墩曲率分布

为阐明圆端形空心墩试件开裂行为、塑性铰机理及曲率分布特性，图5.4-2给出了各试件发生首次屈服位移工况及最大位移工况下的裂缝分布。由于墩底倒角上缘薄壁处的M/W最大，其附近区域是出现第一条明显弯曲裂缝的位置，即各试件中的弯曲裂缝C1。与此同时，该区域理论压应力也最大，最大位移工况下混凝土保护层的压溃剥落、纵向钢筋的屈曲断裂均发生在墩底空心段及墩底倒角附近。因此桥墩塑性变形集中在墩底倒角及空心段附近，塑性铰相对普通等截面实体墩整体上移，故区域2平均曲率φ2最大。空心段截面刚度EI0的变化使得墩底倒角以上一定区域L′内的理论M/W也较大，导致桥墩最终裂缝分布也主要集中在该范围内，约占墩身高度的2/3。

由上述分析可知，在进行圆端形空心墩抗震设计时，应尤为注意空心段的底部及顶部连接处构造细节，防止强震作用下墩底形成塑性铰后因混凝土的压溃剥落或纵筋屈曲拉断而导致侧向承载力的急剧下降。

基于试验观测的塑性区域长度通常具有一定的主观性，需要根据实测位移和曲率反算Lp。等截面实体桥墩的等效塑性铰简化模型，如图5.4-3（a）所示，假定Lp范围内的塑性曲率为常数，此时由式（5.4-1）可以确定墩顶极限容许位移。将式（5.4-1）变换为式（5.4-2），即可利用试验所测位移和曲率计算桥墩等效塑性铰长度试验值。

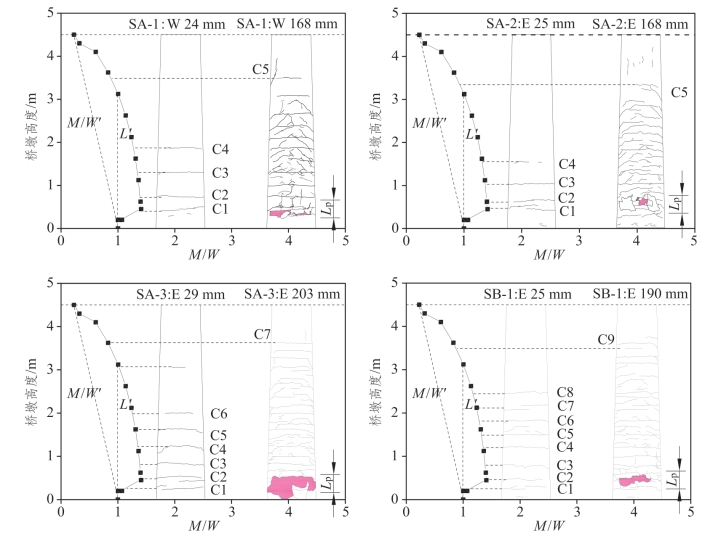
图5.4-2　无量纲应力分布与墩身裂缝联系

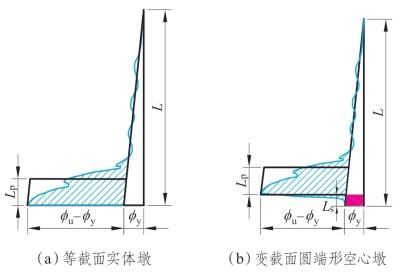
图5.4-3　等效塑性铰长度定义

鉴于铁路圆端形空心墩在塑性演化及曲率分布方面与等截面实体墩存在较大差异，不能直接套用式（5.4-2）计算Lp试验值。故根据墩身曲率分布将原简化模型修正如图5.4-3（b）所示，此时由式（5.4-3）计算圆端形空心墩墩顶位移，由式（5.4-4）得圆端形空心墩等效塑性铰长度试验值。

(www.xing528.com)

根据《铁路工程抗震设计规范》，采用最外层纵筋屈服时的墩顶位移作为屈服位移，同时取承载力下降至峰值承载力80%时的位移作为极限位移，结合实测曲率与位移，计算等效塑性铰长度如表5.4-8所示。

表5.4-8　桥墩等效塑性铰长度

用表5.4-7中公式M1～M12计算4个桥墩模型的等效塑性铰长度，其中桥墩计算高度扣除了墩底实体段高度。各模型塑性铰长度计算结果与实测值的比较如图5.4-4所示，两者比值的平均值和变异系数如表5.4-9所示。分析可知：

（1）各模型塑性铰长度计算值介于200 mm至650 mm之间，将实测值包含在内，说明由于构件类型、设计参数、加载方式等不同，加之各模型中因素取舍不一，所得出公式计算结果存在较大差异。

（2）M1（Mattock）和M12（Telemachos）计算值远大于试验值，可能会高估桥墩的极限容许变形能力，使得桥墩抗震设计偏于不安全。

（3）其余大多数模型预测值均在不同程度上小于试验值，表明相较于一般等截面实体桥墩，变截面的圆端形空心墩塑性铰区域在上移的同时，其塑性演化范围也在增大。

（4）模型M2（Bae和Bayrak）计算结果最为保守，其可能的原因是该模型的推导源于高轴压比（η为0.2和0.5）及高配筋率（ρl为1.25%）的实体截面，而铁路圆端形空心墩模型的轴压比和纵筋率相对较小，使得等效塑性铰长度计算值始终为0.25h。

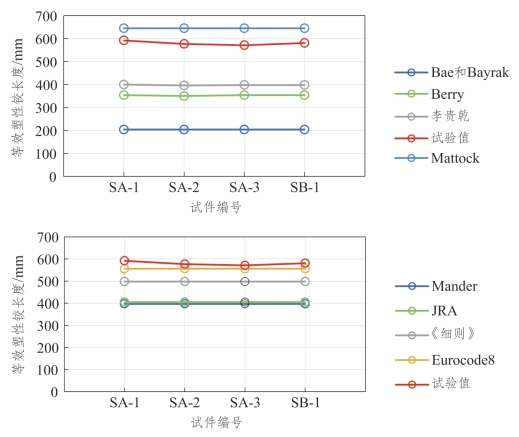
图5.4-4　等效塑性铰长度计算值与试验值比较

表5.4-9　LP计算值与试验值比值平均值和变异系数

M5（Eurocode8）模型能够较好地评估铁路单线圆端形空心墩的塑性铰长度，从抗震设计安全、经济的角度出发，可以用于铁路圆端形空心墩的抗震设计。其余模型对圆端形空心墩的等效塑性铰长度计算值差异较大，这些模型均源于实体规则截面，与圆端形空心截面的受力和塑性特性具有显著差异，同时未考虑到空心墩所设置的倒角过渡段，因此其适用性须审慎处之。