铁路高墩损伤演化过程分析的研究成果报道

为了模拟钢筋混凝土圆端形空心墩的损伤破坏过程，建立了ABAQUS的三维有限元模型，基于损伤本构的桥墩实体单元模型，分析了桥墩在混凝土开裂、钢筋首次屈服，以及极限状态下的损伤机理和损伤演化规律，如图5.3-1所示。根据试验工况逐步施加拟静力荷载（PGA），可以准确预测桥墩的损伤部位，如计算表明实体和空心截面倒角处是桥墩的易损部位，这与实测结果一致，同时ABAQUS模型还准确预测出首次开裂、纵向钢筋首次屈服等状态。

采用SAP2000对2种配重方法、3种模拟方式进行计算，分析了不同墩高、配筋率下墩底空心截面弯矩、塑性转角、墩顶最大位移和加速度、墩底剪力等随PGA增加的变化规律。以非线性动力时程分析为基础，根据具体试验工况，将各试验墩IDA分析的PGA增幅设置为0.05g。改变PGA进行非线性动力时程分析，并记录相关结果。每个动力模型的墩顶位移、加速度与特征截面弯矩、曲率随PGA的变化情况如图5.3-2～图5.3-11所示。

图5.3-1　SA-1混凝土开裂、钢筋首次屈服和极限状态下损伤演化过程

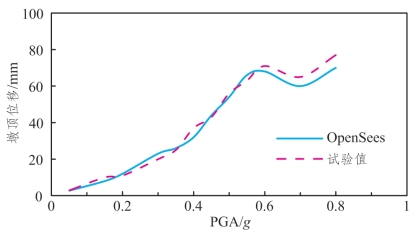
图5.3-2　DB-1墩顶位移随PGA的变化情况

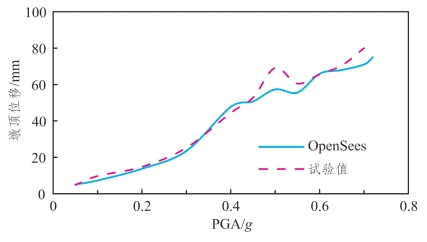
图5.3-3　DB-2墩顶位移随PGA的变化情况

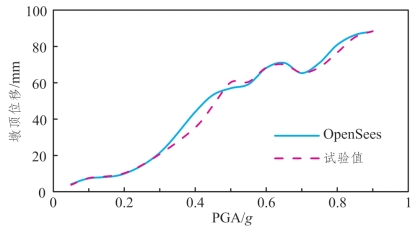
图5.3-4　DB-3墩顶位移随PGA的变化情况

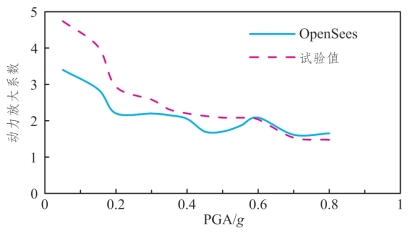
图5.3-5　DB-1动力放大系数随PGA变化情况

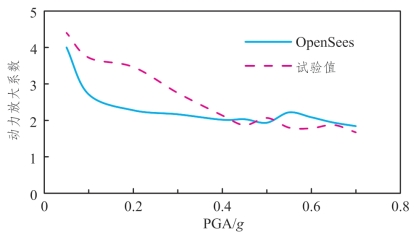
图5.3-6　DB-2动力放大系数随PGA变化情况

(www.xing528.com)

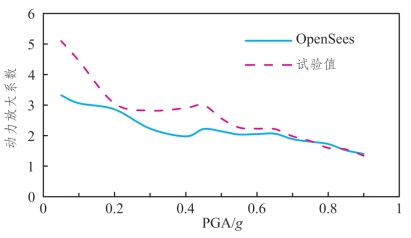
图5.3-7　DB-3动力放大系数随PGA变化情况

图5.3-8　DB-1特征截面弯矩随PGA变化情况

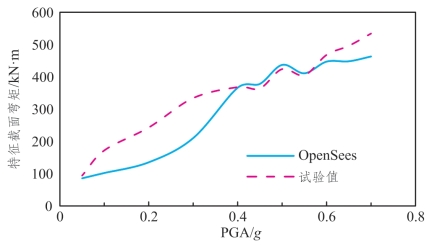
图5.3-9　DB-2特征截面弯矩随PGA变化情况

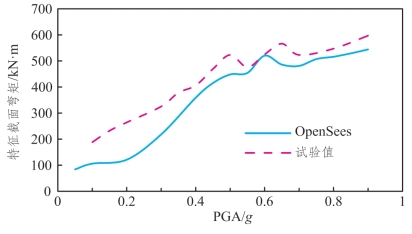
图5.3-10　DB-3特征截面弯矩随PGA变化情况

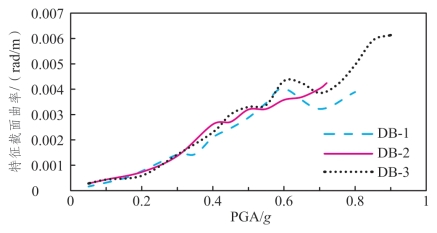
图5.3-11　特征截面曲率随PGA的变化情况

（1）分析图5.3-2～图5.3-4、图5.3-11可发现：各墩数值模拟得出的墩顶位移响应在中低荷载强度下随PGA的增大而增大，当达到一定PGA会出现墩顶位移随PGA增大而减小（或保持平稳）的现象，随后墩顶位移又继续增加；除此之外，各PGA下的墩顶位移试验值与数值模拟值均吻合较好。

（2）分析图5.3-5～图5.3-7可发现：各墩数值模拟得出的动力放大系数整体趋势为随PGA的增大而减小，这一变化规律与试验规律一致。但其各PGA下的动力放大系数，在中低荷载强度下（PGA大概范围为0.05g～0.5g）与试验值有一定差异，数值模拟值小于试验值；在PGA较大时（0.55g～0.9g）其吻合程度较好。

（3）分析图5.3-8～图5.3-10可发现：在中低荷载强度下，特征截面（墩底空心倒角上沿截面）弯矩随PGA的增大而增大；当达到一定PGA后，弯矩值会出现随PGA的增大而减小或增大幅度明显减小的现象（弯矩值保持平稳），继续增大PGA其又会恢复快速增长趋势，这一现象与试验现象一致；但同动力放大系数的规律一样，数值模拟得到的特征截面弯矩在中低荷载强度下比试验值小，在PGA较大时数值模拟结果与试验值又吻合较好。

（4）总地来说，3个圆端形空心高墩的分析结果与试验结果均吻合较好，说明通过OpenSees建立的非线性动力时程模型适用于圆端形空心高墩的抗震性能分析。