3.3.2.1 钢筋混凝土桥墩抗剪能力计算公式介绍
1.各国规范桥墩抗剪公式和学者提出的抗剪公式对比
在基于能力的抗震设计方法中,为了确保钢筋混凝土桥墩具有足够的位移延性能力,要使桥墩抗剪强度大于桥墩可能承受的最大剪力,即桥墩的抗剪能力大于抗剪需求,保证桥墩发生预期的延性破坏模式。下文将详细介绍国内外规范和学者提出的桥墩抗剪能力计算公式。
(1)ACI 318M-05。
美国ACI 318M-05规范是由美国混凝土协会委员会基于相应的报告、研究编写的,此规范采用公制单位。设计截面抗剪强度的验算条件为:
![]()
式中 Vu——设计截面处的剪力需求;
Vn——截面的名义抗剪强度。
其中
![]()
混凝土和抗剪钢筋提供的抗剪强度分别为:

(2)CALTRANS BRIDGE DESIGN SPECIFICATIONS。
美国Caltrans规范由美国加州运输局于2004年2月颁布实施。延性混凝土构件设计截面抗剪强度的验算条件为:
![]()
名义抗剪强度由两部分组成:
![]()
由混凝土提供的抗剪强度要考虑弯曲和轴向荷载的影响。

在塑性铰区内:
![]()
在塑性铰区外:
![]()
以上两个系数的取值分别为:

抗剪钢筋对于抗剪强度的贡献,采用桁架原理考虑。对于矩形截面和圆形截面分别为:

与ACI 318M-05计算模型不同,Caltrans规范是用无量纲系数来反映配箍率、延性和轴向荷载对于混凝土提供的抗剪能力大小的影响,也是Factor1和Factor2存在的意义。Factor1规定其在塑性铰区内下限为0.025,上限为0.25。塑性铰区外则直接取为0.25。Factor2反映的是轴向压应力对于抗剪强度提高的影响,但也有其上限值。当轴向压应力大于6.8 MPa时,认为轴向压应力对于抗剪能力提高的作用已经到顶。
(3)Priestley et al.(UCSD)。
Priestley等学者通过对于ASCE/ACI规范、Ang/Wong和Watanabe/Ichinose等人的研究成果和对于试验数据的分析,提出钢筋混凝土桥墩的抗剪公式由3部分组成。除了混凝土和抗剪钢筋对钢筋混凝土桥墩抗剪强度的贡献外,轴向荷载也对抗剪强度有影响,并且将其独立出来。具体的表达式为:
![]()
对于以上3个部分的影响因素,Priestley等人的研究成果表明:混凝土对于抗剪强度的贡献与混凝土的抗拉强度和桥墩的延性有关;轴向荷载对于抗剪强度的贡献与桥墩的轴向荷载大小和剪跨比有关;而抗剪钢筋对于抗剪强度的贡献与抗剪钢筋的配筋率有关。混凝土提供的名义抗剪强度:

抗剪钢筋提供的名义抗剪强度,对于圆形截面和矩形截面分别为:

轴向荷载提供的名义抗剪强度:

(4)USC Model。
南加州Xiao Yan和Martirossyan等学者在Priestley模型基础之上进行改进,使其能更准确地预测使用高强混凝土情况下的抗剪强度。最明显的改进在于用一个双线性模型来表征位移延性对于抗剪强度的影响。抗剪强度的组成同样分为3部分,由混凝土、抗剪钢筋和轴向荷载的贡献组成。
![]()
混凝土、轴向荷载和抗剪钢筋提供的名义抗剪强度分别为:

(5)Sezen et al.(UCB)。
加州大学伯克利分校的Sezen和Jack P.Moehle等学者提出了与之前不同的模型,其特点在于认为桥墩的位移延性对混凝土和抗剪钢筋提供的抗剪强度均会有影响,并且认为轴向荷载是通过影响混凝土来间接影响桥墩的抗剪强度。其抗剪强度公式为:
![]()
由混凝土和抗剪钢筋提供的名义抗剪强度分别为:
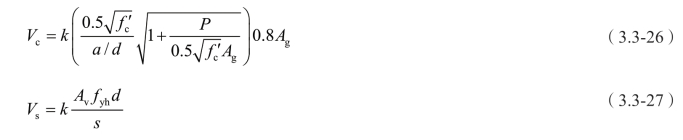
(6)UH Model。
美国休斯敦大学的学者在对已有的抗剪能力计算模型和相应参数的影响规律进行研究的基础上,提出了新的桥墩抗剪能力计算模型。该模型基于Priestley的模型,对位移延性的影响规律进行了细化,并且基于SRCS程序进行仿真计算,通过模型的对比得到了比较好的结果。
![]()
混凝土、轴向荷载及抗剪钢筋提供的名义抗剪强度分别为:
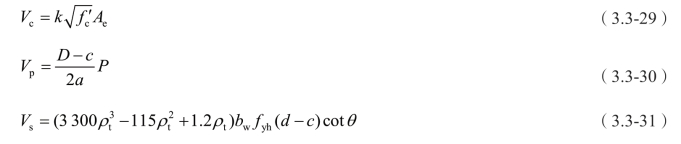
(7)《公路桥梁抗震设计细则》。
2008年版的我国《公路桥梁抗震设计细则》参照《美国加州抗震设计准则》的抗剪能力计算公式,但对其混凝土提供的抗剪能力计算公式进行了简化。桥墩塑性铰区域沿顺桥向和横桥向的斜截面抗剪强度应按下列公式验算:

箍筋提供的名义抗剪能力:

(8)《城市桥梁抗震设计规范》。
2011年版的我国《城市桥梁抗震设计规范》借鉴的是美国AASHTO规范的抗剪能力计算公式。桥墩塑性铰区域沿顺桥向和横桥向的斜截面抗剪能力应按下列公式计算:
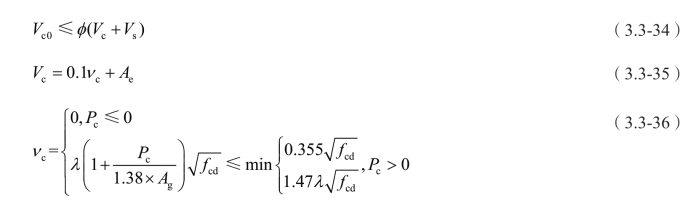
圆形截面和矩形截面抗剪钢筋提供的剪力分别为:

(9)《道路桥示方书·同解说》。
2002年的日本桥梁抗震设计规范《道路桥示方书·同解说》(Ⅴ耐震设计编)认为桥墩截面的横向抗剪能力是由混凝土和横向配筋提供的。


2.抗剪公式的分析与评价
上文提到的多个抗剪公式分别从不同的角度考虑桥墩抗剪能力的计算,计算得到的结果也有差异,本书总结了各抗剪公式中考虑的抗剪强度影响因素如表3.3-1所示。其中,ACI 318M-05认为桥墩的抗剪能力恒定,并不随位移延性的增加而变化,这显然与相应的理论与试验研究不符。而这也是很多国家规范中抗剪能力计算公式的通病,即公式过于保守。这与抗剪机理研究不足、尚未有被一致认可的计算模型有关,同时也导致了设计的不科学和材料的浪费。
表3.3-1 各抗剪强度公式中影响因素统计

相比ACI 318M-05公式,Caltrans公式通过引入系数Factor1和Factor2来考虑箍筋、轴压和位移延性对于混凝土提供的抗剪强度的影响,并且对这2个系数均指定了上下限。由公式(3.3-12)可知,随位移延性的增大,Factor1的取值逐渐变小,位移延性的增大会导致混凝土提供的抗剪能力减弱,这与试验观察是相符的。Factor2用以考虑轴压力对于混凝土提供的抗剪强度的提高作用,其取值的下限和上限分别是1.0和1.5,表明轴压力对于混凝土提供的抗剪能力的最大贡献为150%。抗剪钢筋提供的抗剪能力计算公式与ACI 318M-05规范基本一致。
Priestley等学者提出的计算公式最大特点在于通过一个无量纲系数来考察抗剪能力随着位移延性的增大的折减效应。这也是之后学者提出的计算公式的一个共同特点。另一个特点在于其单独考虑了轴压力对于抗剪能力的贡献。抗剪钢筋提供的抗剪能力计算则通过引入一个系数考虑了斜裂缝的开展方向。
USC模型是在Priestley模型的基础上改进而来,在预测高强混凝土柱的抗剪能力上准确性更高。其计算公式同样是通过一个无量纲系数来考察位移延性对于混凝土提供抗剪能力的折减效应,但这一系数的取值则略有不同。在计算抗剪钢筋提供的抗剪能力时,引入了一个角度来考虑不同的斜裂缝开展方向,而不是引入了一个确定的系数。
Sezen等人提出的模型认为位移延性对于混凝土和抗剪钢筋提供的抗剪能力均有折减作用,并且认为轴压力的存在对于混凝土提供抗剪能力有提高作用。
UH模型是在大量试验数据和参数分析基础之上提出的一个较为复杂的计算模型。其同样引入一个无量纲系数来考虑位移延性对于抗剪能力的折减作用,但计算略为复杂,考虑了箍筋率的影响。抗剪钢筋提供的抗剪能力计算公式是以箍筋率的形式来体现的。
我国《公路桥梁抗震设计细则》和《城市桥梁抗震设计规范》中的桥墩塑性铰区抗剪能力计算公式分别借鉴了美国Caltrans和AASHTO规范,并做出一些改进。其中前者分别计算混凝土和钢筋提供的抗剪强度并通过系数折减再进行组合。与ACI 318M-05规范一样,计算结果偏于保守。后者考虑了轴压力对于混凝土提供抗剪能力的增强作用,计算公式相对复杂,但是同样引入了折减系数。
日本桥梁抗震设计规范提出的抗剪能力计算公式中,通过3个无量纲系数分别考虑往复荷载作用、桥墩截面以及抗拉钢筋对于混凝土提供的桥墩抗剪能力的修正作用,钢筋提供抗剪能力计算与之前的模型类似,考虑了斜裂缝的开展方向。
总体上看,学者提出的计算公式更为复杂,考虑因素更多;而规范提出的计算公式较为简单,也偏于保守。这与二者的适用范围有关。本书将通过模型与试验数据的对比,讨论各个计算模型的合理性。(https://www.xing528.com)
本书选取5个下载自太平洋地震工程中心(PEER)的试验桥墩作为实例,比较上文所列公式的准确性,5个桥墩的参数见表3.3-2。
表3.3-2 各桥墩实例的参数
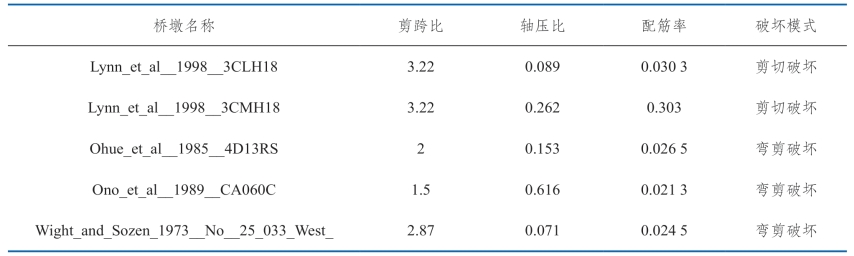
根据所列9个国内外抗剪能力计算公式分别计算桥墩抗剪能力曲线,并与试验所得需求曲线进行对比,结果如图3.3-7~图3.3-11所示。
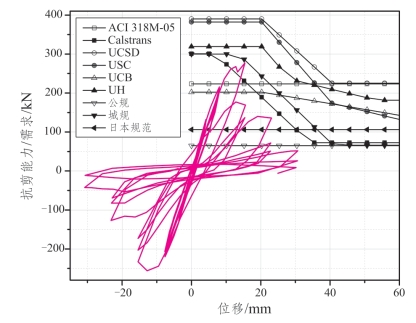
图3.3-7 Lynn_et_al__1998__3CLH18 抗剪能力/需求对比
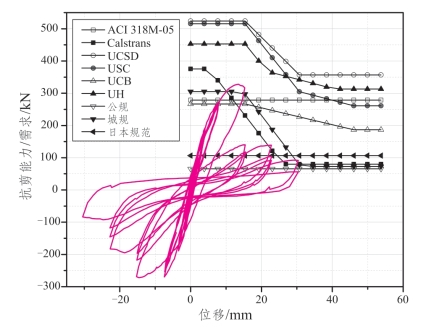
图3.3-8 Lynn_et_al__1998__3CMH18 抗剪能力/需求对比
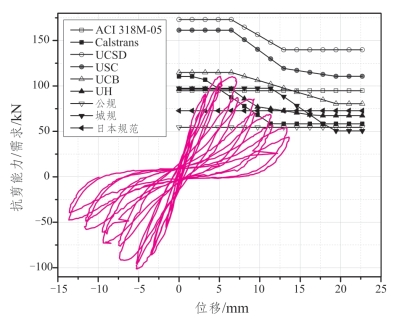
图3.3-9 Ohue_et_al__1985__4D13RS 抗剪能力/需求对比
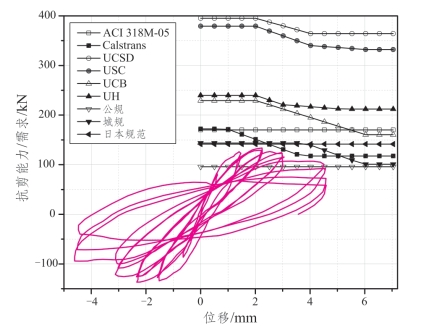
图3.3-10 Ono_et_al__1989__CA060C 抗剪能力/需求对比
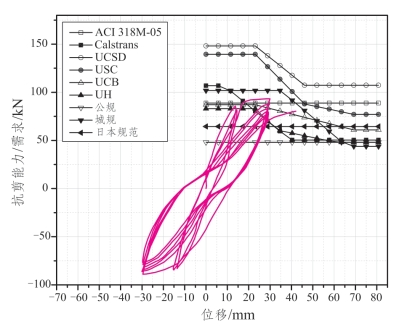
图3.3-11 Wight_and_Sozen_1973__No__25_033_West_抗剪能力/需求对比
上文所列的5个试验桥墩参数覆盖范围是:剪跨比1.5~3.22、轴压比0.071~0.616、配筋率0.021~0.3,有一定的代表性。从图示可知,各抗剪计算公式对同一桥墩得到的计算结果差异很大,国内外学者提出的抗剪计算公式总体高估了桥墩的实际抗剪能力,而各国规范所提出的抗剪计算公式则偏于保守,加之折减系数的考虑,计算结果相较试验结果偏低。各国规范公式本身并不能准确反映桥墩抗剪能力随着延性增大的变化规律,这就导致试验桥墩在加载后期,计算结果与实际的抗剪能力差异越来越大。而且,现有计算公式多用一个与桥墩参数无关的系数来考虑桥墩抗剪能力随位移延性增大的变化趋势,并不能完整反映抗剪能力变化与桥墩位移延性增大的关系。对于不同的试验桥墩,同一抗剪计算公式计算结果趋势也并不完全一致,即同一抗剪公式对于不同参数桥墩的抗剪能力的适用性有待进一步研究。
综上,准确预测钢筋混凝土桥墩的抗剪能力对于桥墩能力设计思想的实现、保证桥墩具有相应的抗剪强度以及保证其在相应地震作用下发生预期的延性破坏都具有重要意义。
3.3.2.2 桥墩抗剪能力计算方法研究
基于截面分析的方法,并考虑剪跨比的影响,提出了桥墩抗剪能力计算公式。式中桥墩的抗剪能力V包括3部分内容:混凝土提供的抗剪能力Vc、箍筋提供的抗剪能力Vs,以及关于剪跨比的影响系数k,具体形式为:
![]()
1.混凝土提供的抗剪能力
以同时受轴压力和侧向力作用的桥墩上某一混凝土单元的受力状态为例进行分析,如图3.3-12所示。
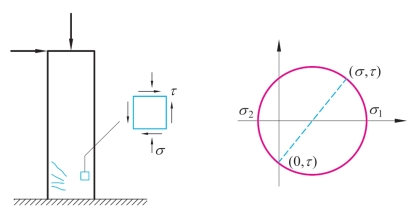
图3.3-12 混凝土二维应力状态和莫尔应力圆表示
考虑混凝土单元同时受到压应力和剪应力作用,分别用σ和τ表示。根据二维应力状态下莫尔应力圆理论,可以计算该单元的两个主应力如下:

随着侧向力的增大,单元受力状态也会发生变化。两个主应力的绝对值随着莫尔应力圆直径的增大而增大,并最终到达混凝土单元的破坏面。考虑约束混凝土本构模型,可以计算得到混凝土的峰值抗压强度作为单元的受压破坏面。考虑二维应力状态下混凝土强度的软化效应,可取混凝土单元的受拉破坏面为:
![]()
将2个破坏面代入主应力的计算公式,可以得到抗拉和抗压破坏时,正应力和剪应力的计算方法。

联立式(3.3-45)和式(3.3-46),可解出单元应力状态分别达到2个破坏面时,剪应力的大小:
![]()
![]()
式中,cτ和tτ分别代表了由抗压破坏面和抗拉破坏面控制的混凝土单元抗剪能力。
根据平面应力单元的主应力与各方向应力的关系,对于某一个混凝土单元,控制剪应力为cτ和tτ的较小值:
![]()
式中,fτ代表了某个混凝土单元所能承受的最大剪应力。桥墩中某一个截面的应力分布可通过应力分析得到。
矩形截面随着截面变形的增大,应变分布规律也发生变化,图3.3-13中N.A.为截面中性轴。中性轴以上表示截面受压区,中性轴以下表示截面受拉区。选取桥墩的临界截面,可通过确定桥墩截面的曲率,计算其应变分布,并通过本构关系分别计算钢筋和混凝土的应力分布。图中C表示截面受压区的高度,可通过截面内力平衡计算得到。
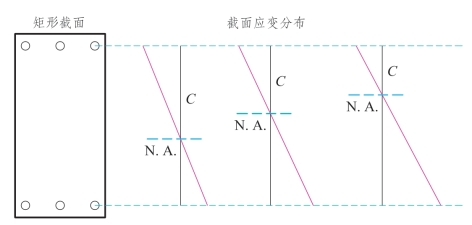
图3.3-13 矩形截面应变分布规律
对于某一转角,通过二分法计算受压区高度能够快速收敛。在得到沿截面高度混凝土的应力分布之后,由混凝土的二维应力分析即可计算得到混凝土单元提供的抗剪能力,沿截面高度积分,就可得整个截面的抗剪能力。取混凝土单元的高度为dz,则抗剪能力为:
![]()
沿截面高度积分:
![]()
式中 Vc——混凝土提供的抗剪能力。
基于平面分析计算所得的抗剪能力,可追踪桥墩受力过程中抗剪能力的变化规律,相比于依据试验破坏桥墩数据所得的抗剪能力计算公式,物理意义更为明确。对截面应力的考察,也包含了轴压力对于桥墩的影响。通过对截面转角增量的选取,可控制计算步长和计算精度。
2.箍筋提供的抗剪能力
既有抗剪计算公式和试验表明,箍筋提供的抗剪强度对于混凝土开裂之后的侧向承载力十分重要,且与平行于剪切方向的箍筋面积、箍筋屈服强度以及箍筋间距等有关。抗剪计算公式中对箍筋部分的考虑可总结为:
![]()
式中:Av为平行于侧向力方向的箍筋面积;fy为箍筋的屈服强度;d为截面的有效高度;s为箍筋间距;α为箍筋提供抗剪能力的修正系数,用来考虑桥墩轴线与斜裂缝之间的夹角以及箍筋提供抗剪能力的折减。依据钢筋混凝土结构受剪桁架模型,取桥墩轴线与斜裂缝之间的夹角为30°。随着侧向力的增大,混凝土开裂和压碎伴随着箍筋的外鼓和拉断,而箍筋提供的抗剪能力也会减小。为简便考虑,引入系数Ks来表征Vs的折减:

式中,右侧表示混凝土提供的抗剪能力在受压区混凝土进入软化段之后的折减率。
![]()
式中,ρp定义为平行于侧向力方向的箍筋率,bw为垂直于加载方向截面宽度,将其代入式(3.3-53),最终箍筋提供的抗剪能力为:

式中,θ取为30°。
3.剪跨比影响系数k的研究
既有研究表明,剪跨比对桥墩的抗剪性能有重要影响,随着剪跨比的增大,桥墩抗剪能力逐渐减小。因此,剪跨比影响系数与剪跨比成反比。k代表剪跨比影响系数,研究给出k值的计算公式如下:

式中,β、γ为常数,λ为剪跨比。
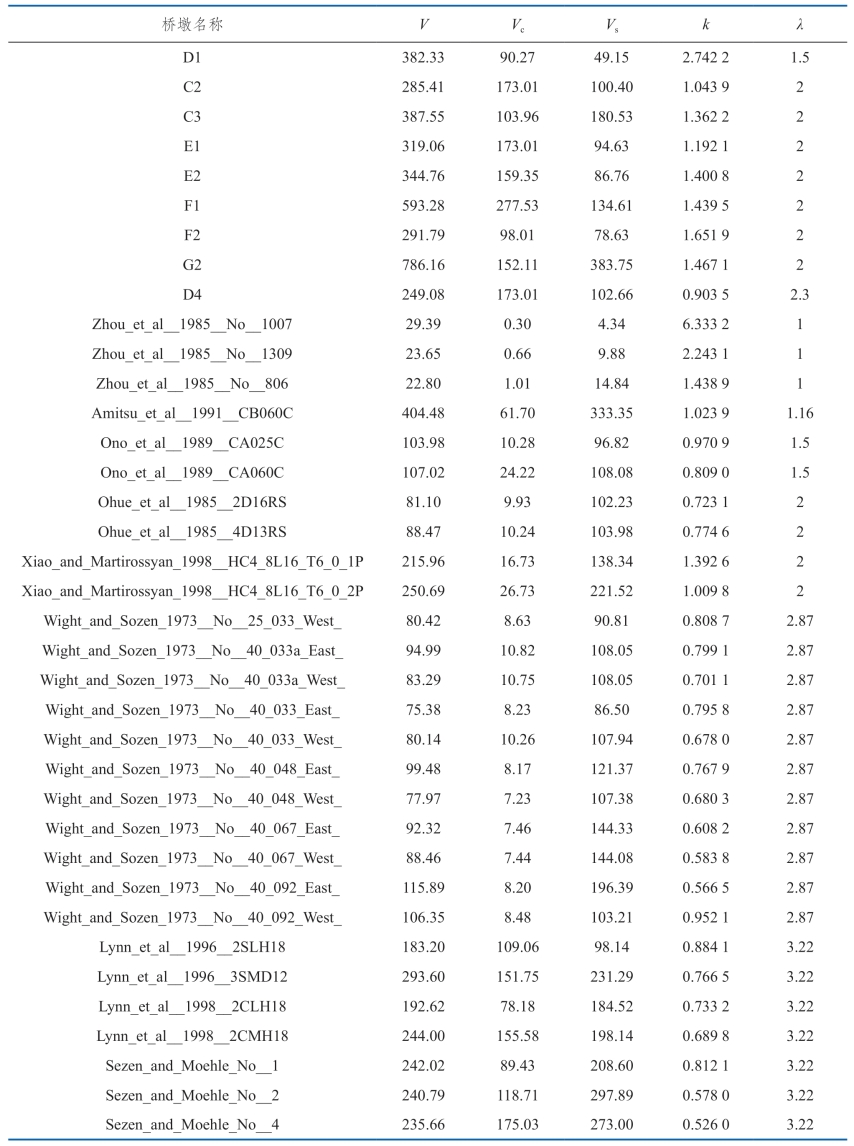
通过试验数据的回归分析,利用最小二乘法,即可得到β、γ的值。回归分析所需数据如表3.3-3所示。
经过回归分析,最终β的估计值为0.439 2,γ的估计值为0.083 4,相关系数为0.763 5。从3.2节中拟静力试验结果可看出,试验桥墩弯剪破坏均发生在剪跨比小于3.0时,因此在计算桥墩抗剪强度时,仅在桥墩剪跨比1≤λ≤3时,对桥墩的抗剪能力进行修正。
综上所述,基于截面分析的钢筋混凝土桥墩抗剪能力计算过程如下:
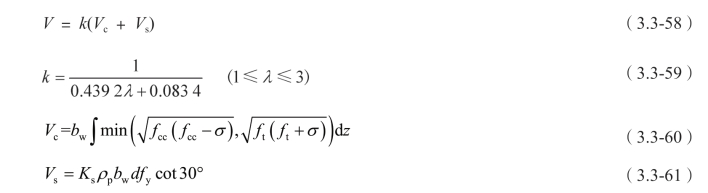
根据试验结果分析可知,在截面面积和截面高度相等的情况下,圆端形桥墩的抗剪性能与矩形桥墩的抗剪性能基本相同,因此本公式不仅适用于矩形桥墩,也适用于圆端形桥墩。
表3.3-3 回归分析数据
3.3.2.3 计算方法的准确性验证
本书根据上述基本原理,使用Matlab编写了程序对钢筋混凝土桥墩抗剪能力进行计算。本节选取太平洋地震工程中心Column Database上20个矩形截面钢筋混凝土桥墩,计算了其抗剪能力,并与试验数据进行对比。由于数据较多,仅选取3组桥墩数据结果进行对比,结果如图3.3-14~图3.3-16所示。
利用本书提出的抗剪能力计算方法得到的桥墩抗剪能力曲线能够很好地反映桥墩的实际抗剪特性。尤其是在桥墩破坏后期,计算模型的结果与桥墩的力-位移曲线的下降段吻合度较高,能够反映加载后期的破坏过程中桥墩的抗剪能力的变化规律。与既有抗剪计算公式的对比也表明,该方法计算结果更为准确,同时对于加载后期桥墩的抗剪能力的变化规律也能更好地反映。
通过与20个参数分布广泛的桥墩试验数据进行对比,验证了本书所提出的计算模型能够准确计算桥墩的抗剪能力随着桥墩位移延性的变化规律。相比既有计算公式,计算原理更为合理,且计算结果更为准确。
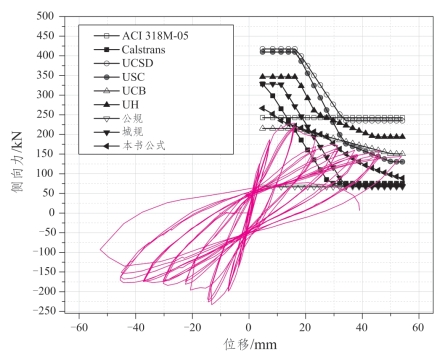
图3.3-14 Lynn计算结果与试验结果的对比
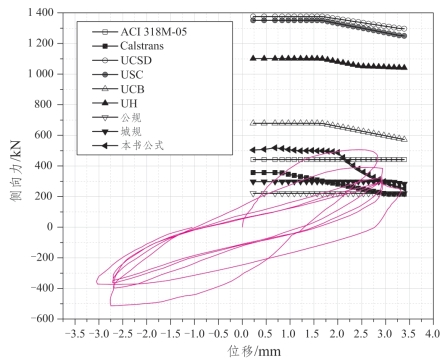
图3.3-15 Amitsu计算结果与试验结果的对比
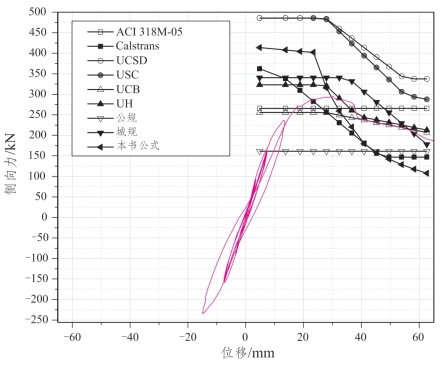
图3.3-16 Sezen计算结果与试验结果的对比
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




