RBF神经网络原理与城市轨道交通安全技术研究

1.RBF神经网络概述

1985年，Powell提出了多变量插值的径向基函数（Radial-Basis Function，RBF）方法。1988年，Broomhead和Lowe首先将RBF应用于神经网络设计，构成了径向基函数神经网络，即RBF神经网络。其基本思想是：用径向基函数（RBF）作为隐单元的“基”构成隐含层空间，对输入矢量进行一次变换，将低维的模式输入数据变换到高维空间内，通过对隐单元输出的加权求和得到输出。

径向基函数（RBF）神经网络是一种新颖有效的前馈式神经网络，它具有最佳逼近和全局最优的性能，同时训练方法快速易行，不存在局部最优问题。这些优点使得RBF网络在非线性时间序列预测中得到了广泛的应用。

2.RBF神经网络的网络结构

RBF网络是一种3层前向网络：第一层为输入层，由信号源节点组成；第二层为隐含层，隐单元的变换函数是一种局部分布的非负非线性函数，它对中心点径向对称且衰减，隐含层的单元数由所描述问题的需要确定；第三层为输出层，网络的输出是隐单元输出的线性加权。RBF网络的输入空间到隐含层空间的变换是非线性的，而从隐含层空间到输出层空间的变换是线性的。不失一般性，假定输出层只有一个隐单元，令网络的训练样本对为{Xn,dn } (n=1,2,…,N)，其中Xn=[x n1,xn2,…,xnM ]T ,(n=1,2,…,N)为训练样本的输入，d n(n=1,2,…,N)为训练样本的期望输出，对应的实际输出为Yn (n=1,2,…,N)；基函数φ(X ,ti)为第i个隐单元的输出，ti=[t i1,ti2,…,tim,…,tiM ](i=1,2,…,I )为基函数的中心；wi (i=1,2,…,I)为第i个隐单元与输出单元之间的权值。

当网络输入训练样本Xn时，网络的实际输出为：

普通RBF网络采用的是高斯函数。“基函数”采用的高斯基函数具备以下的优点：

（1）表示形式简单，即使对于多变量输入也不增加太多的复杂性。(www.xing528.com)

（2）径向对称。

（3）光滑性好，任意阶导数均存在。

（4）由于该基函数表示简单且解析性好，因而便于进行理论分析。

RBF神经网络结构如图4-15所示。

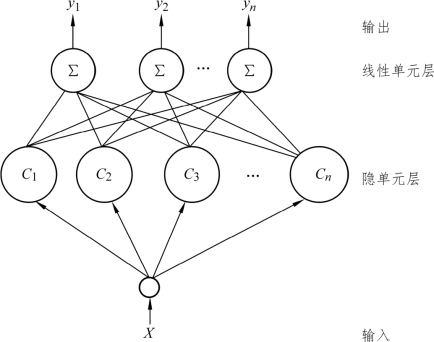
图4-15　RBF神经网络结构

RBF网络具有良好的逼近任意非线性函数和表达系统内在的难以解析的规律性的能力，并且具有极快的学习收敛速度。