城市轨道交通安全研究：基于D-S证据理论和信息熵的融合方法

1.D-S证据理论

D-S证据理论最早应用于专家系统中，其最大特点是在证据中引入了不确定性，建立了基本概率分配函数、信任函数、似然函数等满足比概率论弱的公理，放松了传统Bayes理论需要完整的先验概率和条件概率知识以及需要有统一的辨识框架要求，可对相互重叠、非互不相容的命题进行证据组合。

基本概率分配函数M：设Ω是样本空间，Ω由一些互不相容的陈述构成。这些陈述的各种组合构成幂集2Ω，定义基本概率分配函数M:2Ω→[0,1]，即M为2Ω到区间[0,1]的映射，满足以下条件：

（1）不可能事件的基本概率是0，即M(∅)=0；

（2）2Ω中全部元素的基本概率之和为1，即∑M (A)=1,A⊆Ω,M (A)为A的基本概率数，表示对A的精确信任。

命题的信任函数Bel：对于任意假设而言，其信任度Bel()A定义为A中全部子集对应的基本概率之和，即

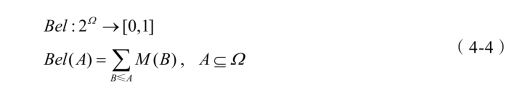
Bel函数也称为下限函数，表示对A的全部信任。由概率分配函数的定义容易得到：

命题的似然函数PI，也称为上限函数，表示对A非假的信任程度，即表示对A似乎可能成立的不确定性度量，满足以下条件：

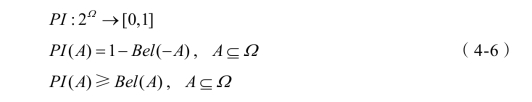
D-S证据理论的合成规则：设有n个证据在Ω上提供的基础概率分配分别为M 1,M2,…,Mn ，D-S证据组合规则给出，这n个证据组合后得到在样本空间Ω上的基础概率分配的计算式为：(www.xing528.com)

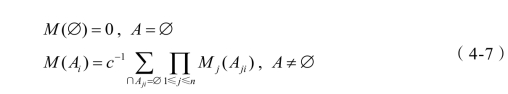
其中，；iA，Aji均为Ω中的焦点元素；=1,2,,

i…K，K为Ω中焦点元素的数目；j=1,2,…,n，n为证据数。

2.信息熵理论

信息熵理论的核心思想是人们能够根据决策中获取信息的数量和质量，提高决策的精度和可靠性，在指标的权重确定方面具有客观性强的优势，其基本原理就是某项指标的值变异程度越大，信息熵越小，该指标提供的信息量就越大，相应指标权重就越大，反之则越小。其计算过程如下：

假设在m项指标、n个被评价对象的评价体系中，原始评价矩阵为Dnm，对其进行标准化处理后得到规范化矩阵Rnm，根据信息熵理论确定熵权的公式，由式（4-8）计算得到第j项指标的熵值，由式（4-9）计算得到第j项指标的熵权，即权重jω。

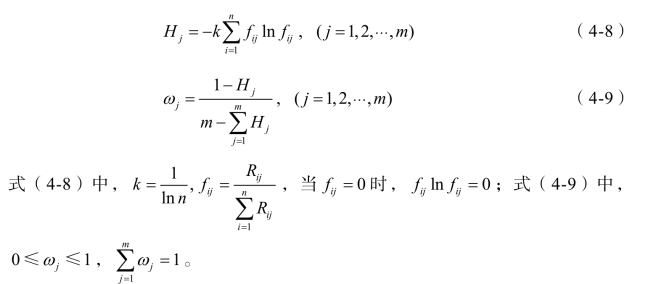
3.D-S证据理论和信息熵融合的城市轨道交通安全预警方法

D-S证据理论不需要大量训练数据，避免了Bayes理论需要完整的先验概率和条件概率知识的限制，但需要获得各预警指标的权重；而信息熵理论在确定权重方面能充分利用预警对象本身的数据信息，克服专家确定权重的主观性，具有随着数据对象变化权重自动动态调整的优势。将两者融合后的城市轨道交通车站安全预警方法如图4-4所示。

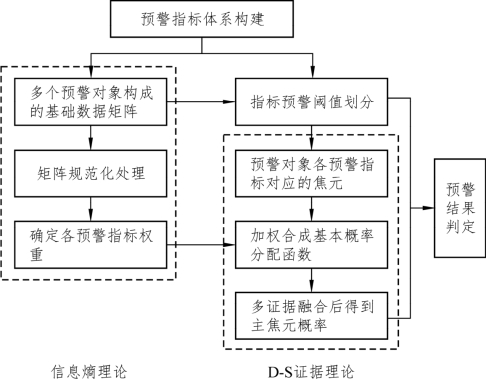
图4-4　证据理论和信息熵融合的城市轨道交通安全预警方法体系