基于抛物线理论的解析法是一种近似方法,状态方程为一元三次方程[6-7],使用时受到小垂度限制,即最大垂跨比不超过1/10,此时误差一般可控制在5%以内。但在大垂度情况下,此法的计算误差较大,且无法准确计入锚跨对承载索的受力影响。当荷重点不在跨中时,索力并不连续。而承载索是一根连续索,在塔顶索鞍和荷重跑车处,都应满足索力连续的条件。当工作跨荷载出现变化时,缆索在塔顶索鞍处会前后滑动,锚跨缆索会做出相应调整,使其索鞍前后的索力相等(不计索鞍滑轮摩擦的情况)。所以当荷重跑车不在跨中时,需要牵引绳提供的拉力来保持跑车的平衡,否则跑车会自动溜滑至跨中平衡位置。
有限元计算中通常采用悬链线索单元模拟缆索,悬链线索单元是以悬链线理论建立的两节点单元,不受小垂度限制,但无法考虑索力连续的问题。相关文献[9-11]各自提出了一种通过调整单元无应力索长使其索力连续的算法,但仅适用于索鞍处,求解荷重跑车处索力连续的问题时不易收敛。相关文献[1112]提供了一种索-轮单元,能计算索鞍处缆索滑移的情况,相关文献[13]提供了一种索-轮单元,能计算滑轮在索长滑行的情况。为了便于区分,将相关文献[11]索-轮单元称为正索-轮单元,用符号“P”表示;相关文献[13]的索-轮单元称为倒索-轮单元,用符合“N”表示。本节基于上述两种索-轮单元研究承载索的几何非线性有限元计算方法,以准确分析缆索吊机承载索的受力情况。
7.3.2.1 正索-轮单元
正索-轮单元是一个三节点平面索单元[14],如图7-18所示,两端节点分别用I、J 表示,中间节点O 为滑轮中心,索从滑轮上方绕过,被分成两个悬链线索段,A、B 为索与滑轮的切点,两侧索段可沿中间滑轮滑动。在平衡状态时,若不计滑轮的摩擦作用,滑轮两侧的索力是相等的,即应满足索力连续的条件。
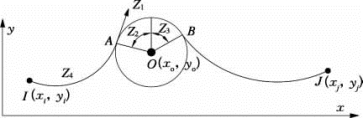
图7-18 正索-轮单元
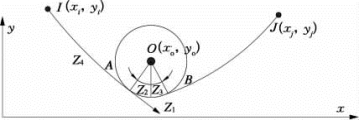
图7-19 倒索-轮单元
7.3.2.2 倒索-轮单元
倒索-轮单元同样是一个三节点平面索单元[13],如图7-19所示,两端节点分别为I、J,中间节点O 为滑轮中心,索从滑轮下方绕过,被分成两个悬链线索段,两侧索段可沿中间滑轮滑动。在平衡状态时,如果不计滑轮的摩擦作用,滑轮两侧的索力是相等的。
7.3.2.3 索-轮单元滑移平衡方程推导
由于滑轮尺寸相对缆索长度比较小,可忽略滑轮半径的影响。对于给定的节点坐标和单元特性(如弹性模量E、截面面积A、自重荷载集度w、无应力索长L0等),单元几何形状需四个独立变量(Z1、Z2、Z3、Z4)才能确定。Z1为I-A 索段A 点处的张力;Z2、Z3为索与滑轮的切点绕滑轮中心与竖直轴形成的夹角;Z4为I-A 索段的无应力索长,独立变量的选取并不唯一,但利用上述变量推导的表达式最为简洁[15]。单元处于平衡状态时,存在唯一Z 值与之对应,但任意给定一个Z 值,单元不一定处于平衡状态,I、J 节点会产生位移,这里称为节点位移残差向量R。类似两节点悬链线索单元,索-轮单元两侧索段可分别建立各力素(索端力向量p、f)和几何变量(索段跨度lx与高差hy)之间的关系方程组,对此方程组取全微分[16],便可得出位移差R 与独立变量Z 的关系函数R(Z)。如不考虑滑轮半径的影响,正倒索-轮单元的R(Z)表达式相同:
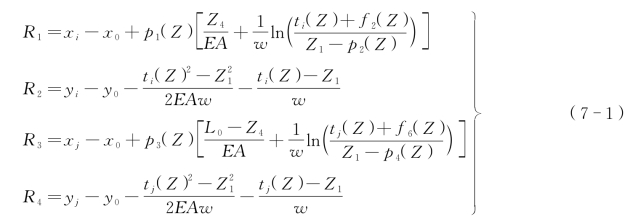
式中 p(Z)——单元A、B 点索端力向量,见式(7-2);
f(Z)——单元I、J 点索端力和滑轮中心O 节点力组成的向量,见式(7-3);
t(Z)——单元I、J 点索端拉力,见式(7-4)。
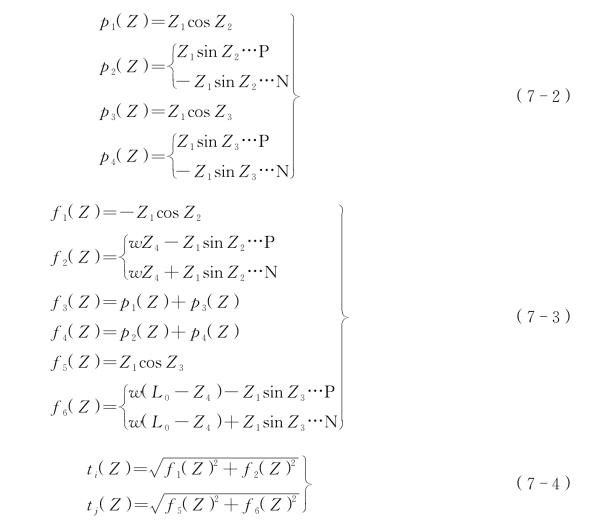
索-轮单元滑移平衡方程可表示为一组非线性方程组,即
7.3.2.4 单元平衡方程的求解
![]()
独立变量Z 发生微小变化ΔZ 会引起节点位移残差R 变化ΔR,其关系近似为
![]()
式中 J——4×4的雅可比矩阵。
将函数R(Z)对变量Z 微分,使位移残差R 最小的ΔZ 为[13-14]
![]()
平衡方程R(Z)=0可采用“N-R法”迭代求解,直至位移残差变化量ΔR 小于设定的允许值,即可认为索-轮单元处于平衡状态。值得注意的是,若初值不合适,迭代计算很难收敛,根据反复调试,Z 的初值按照以下方法确定时,各种情况下的迭代计算基本能够收敛:

式中 lIA——单元索段I-A 的弦长;
l——单元索段总弦长。
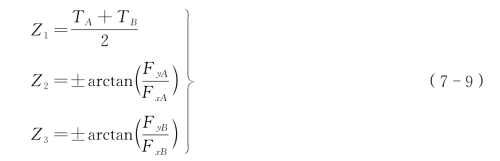
根据式(7-8),可确定单元两侧索段的无应力索长,将两侧索段分别当成两节点的悬链线索单元,再利用两节点悬链线索单元的索端力柔性迭代程序,可分别计算出A、B 点处的索端力向量F和拉力T。不妨令
 (https://www.xing528.com)
(https://www.xing528.com)
其中,正索-轮单元Z2取正,Z3取负;倒索-轮单元相反。按照上述方法事先经过一次索端力柔性迭代计算,虽然增加了计算次数,但能保证收敛,避免了反复调试初值。
值得注意的是,正索-轮单元在索处于松弛状态时可能存在三个平衡状态,工程上的索结构通常是处于较为张紧的状态,一般不会出现此种情况。根据索-轮单元滑移平衡方程R(Z)=0求解的结果,可以计算出单元的切线刚度矩阵Ke。
7.3.2.5 承载索的几何非线性计算程序
(1)有限元模型的建立。利用正索-轮单元模拟锚跨与塔顶索鞍,倒索-轮单元模拟工作跨与荷重跑车。实际上,当荷重跑车不在跨中时,跑车的平衡需要依靠牵引绳提供的拉力来平衡,为简化计算模型,通过荷重点的水平位移约束近似模拟牵引绳的作用,若需要精确考虑,可以正索-轮单元或两节点悬链线单元模拟牵引绳。图7-20为典型的单工作跨缆索吊机承载索的有限元计算模型。同理,可建立双工作跨和多工作跨的计算模型。
(2)计算程序编制。根据虚功原理建立平衡迭代方程,采用“N-R 法”迭代求解非线性方程组。使用MathCAD工程数学软件编写计算程序,如图7-21所示。

图7-20 单工作跨的缆索吊机承载索有限元计算模型
温度荷载[17]可以通过改变单元无应力索长L0和自重荷载集度w 的方式来考虑:
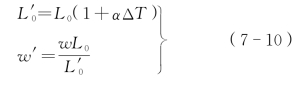
式中 α——温度线膨胀系数;
ΔT——温差。
(3)缆索初始状态求解。缆索在进行非线性计算时,需给出索-轮单元的无应力索长。通常将最大吊重时的缆索垂度作为控制参数。先取工作跨缆索进行计算,以最大垂度fmax作为目标,采用“二分法”搜索工作跨无应力索长;然后分别分析两侧锚跨缆索,根据索鞍处索力连续条件,可得出锚跨在索鞍处的拉力T,以此拉力T 为目标,采用“二分法”搜索锚跨的无应力索长。将各段的无应力索长求和得出缆索的总无应力索长,再按各单元弦长比例分配即可。通常无应力索长L0的初始范围可根据下式确定:
![]()
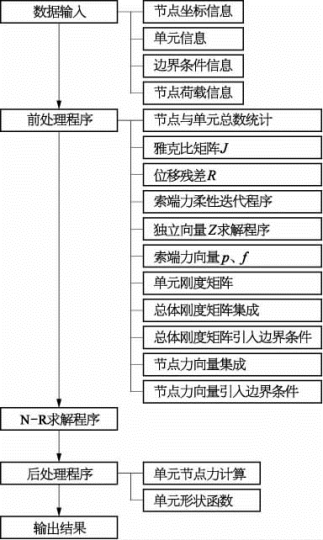
图7-21 承载索几何非线性计算程序
式中 l——索段弦长。
7.3.2.6 与解析解对比分析
缆索吊运系统承载索为两组,每组承载索由8根φ50密封钢丝绳组成,设计最大吊重垂度40 m,最大起重量1 000 kN。取单根钢丝绳进行计算分析,其中弹性模量E=160 000 MPa,索截面面积A=1 790 mm2,索自重荷载集度w=0.143 kN/m,荷重点荷载P=178.3 kN。以最大吊重时跑车位于跨中处作为初始状态,用“二分法”求得缆索的无应力总索长为1 450.633 m。实际上,工作跨缆索上存在两个荷重跑车,其间距为20 m,但跑车间距相对索的跨径较小,已有研究验证了这种情况对索的受力影响很小,可以视为单个荷重点分析。
为验证上述非线性有限元计算程序的正确性,以合江长江一桥为依托,将有限元计算结果与解析法计算结果进行对比,计算结果见表7-1、表7-2。其中,状态A代表最大吊重时,荷重跑车位于跨中工况;状态B代表无荷初始安装状态工况;状态C代表最大吊重时,荷重跑车位于距离左岸塔架40 m处工况。
表7-1 解析法与有限元法计算结果对比
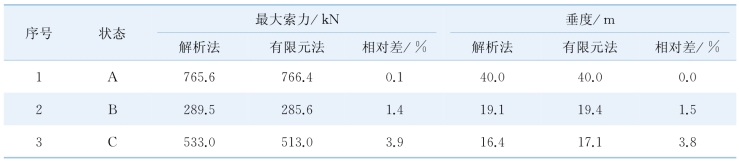
表7-2 状态C的有限元非线性计算结果
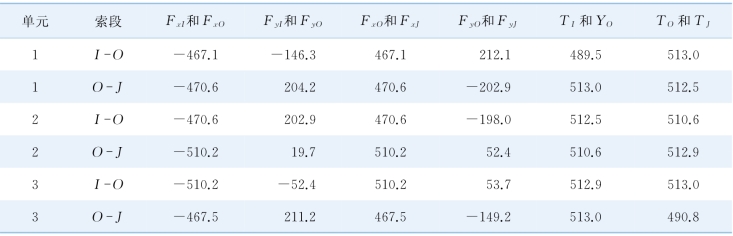
从表7-1可知,两种计算方法的结果存在一定差异。状态A解析法和有限元法的最大索力和垂度的计算结果基本一致;状态B解析法和有限元法的最大索力和垂度的计算结果相对差分别为1.4%和1.5%;状态C解析法和有限元法的最大索力和垂度的计算结果相对差较状态A 和B大,分别为3.9%和3.8%,均在工程可接受范围内。状态A和状态B存在差异主要是因为抛物线理论与悬链线理论本身存在差异,小垂度状态下,两种理论的差异并不大,但随垂度的增大,这种差异造成的影响会增大。状态C计算结果存在差异的主要原因除了抛物线和悬链线理论外,更受到能否满足索力连续条件的影响,故其差异较状态A和状态B大。
另外,分析状态C可知,荷重跑车越靠近塔架索鞍,其解析法和有限元法计算结果差异越大,在跨中时最小,如图7-22、图7-23所示。图中,X 为荷重跑车距离塔架索鞍的水平距离,Tmax为最大索力结果,e为相对差。
由图7-22还可以看出,在距离塔架索鞍15 m 处,两种方法的索力相对差为8.1%,垂度相对差为10.4%,误差已超出了工程可接受限度。但由于此时的索力并不是缆索处于最大索力状态时刻的索力,此差异并不影响缆索本身的强度验算结果,但对塔架以及缆风绳的计算会有一定影响。另外,由表7-2可知,本节的算法可以满足索力连续条件,反映了不考虑索力连续条件的计算方法的局限性,以及本节索-轮单元法计算的必要性。
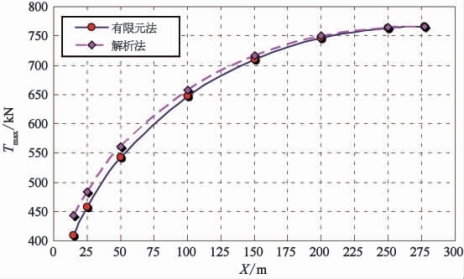
图7-22 状态C荷重跑车移动时索力变化
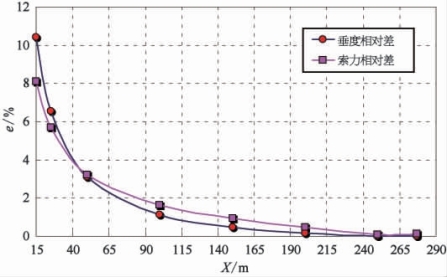
图7-23 状态C两种方法计算结果差异变化
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




