500米级钢管混凝土拱桥建造创新技术及施工优化计算方法

为确保超大跨径拱桥的线形、扣索力及拱圈应力满足要求，以在建世界最大跨径拱桥平南三桥为工程背景，采用大型空间有限元软件midas Civil建立空间有限元模型，基于“过程最优，结果可控”一次张拉施工优化计算方法进行理论分析，从施工过程中的拱圈线形、最大应力和扣索力等多个方面分析了拱圈施工的安全性和合理性。

5.3.3.1　工程概况

主桥拟采用220 t缆索起重机安装，钢绞线进行斜拉扣挂施工，塔机采用装备化钢塔架；引桥拟采用盘扣式满堂支撑架现浇（图5-21）。

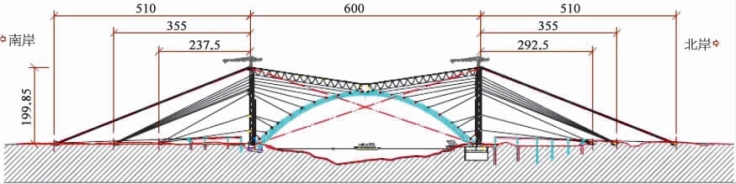
图5-21　平南三桥结构示意图

拱肋节段如图5-22所示。单侧主拱肋共分为22个节段，以桥梁中心线对称布置，两岸以跨径中心对称，全桥共计44个节段。拱肋中距30.1 m，桥面以上每一节段间均设一道I形横撑和一道三角形横撑，共计16道（不含拱脚处横撑）。

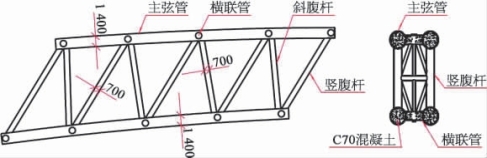
图5-22　拱肋节段示意图

5.3.3.2　计算参数

主拱肋吊装采用midas Civil 2015软件进行分析计算，该模型的各建模参数如下。

1）材料参数、截面参数和单元类型

通过midas Civil 2015对平南三桥拱肋吊装进行建模分析计算，拱肋采用梁单元进行模拟，扣索采用桁架单元进行模拟。主要单元的类型、材料名称和截面形状尺寸见表5-4。

表5-4　主要杆件截面统计

（续表）

2）拱肋节段自重

钢材基本容重取78.5 kN／m3，针对主拱圈、塔架等构造中设置的节点板、横隔板、焊缝等难以在有限元模型中体现的重量，通过容重换算方式予以反映。midas建模中拱肋钢材容重取为83.22 kN／m3，经计算，平南三桥主拱钢材换算容重为1.060 12。

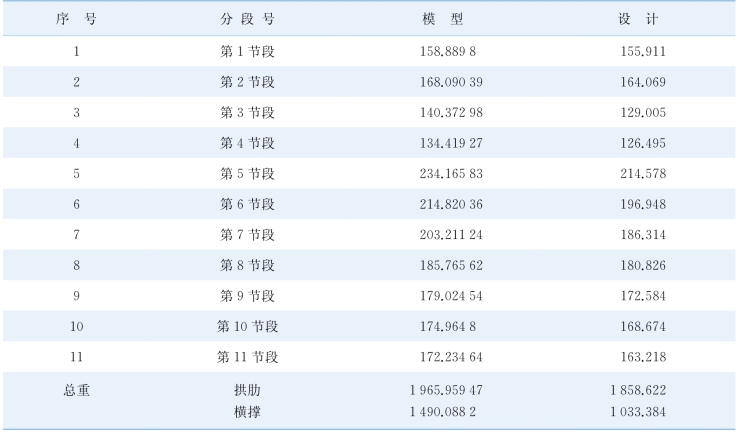
表5-5给出的是模型中拱肋节段重、横联重和设计图纸给出的拱肋节段重、横联重。由计算结果表明，经过修正后的钢材容重，在模型中计算出来的拱肋节段重和横联重均略大于设计图纸计算出来的重量，这多出的部分可用于抵偿护栏、焊接机械等其他不可预见的重量，使模型与实际尽可能相同。

表5-5　拱肋节段质量统计　单位：t

3）扣索参数

该桥扣索采用φ15.2 1 860 MPa高强度低松弛钢绞线，弹性模量E＝1.95×108kN／m2，锚固端采用低应力锚具，设置于吊装的拱肋节段端头附近的扣点结构。南岸扣挂体系示意如图5-23所示。

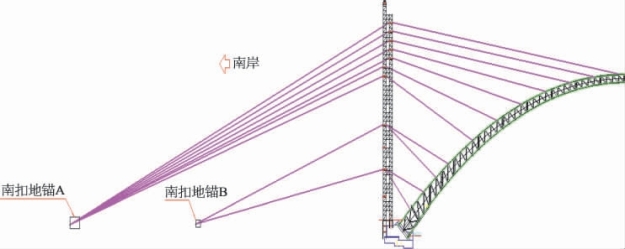
图5-23　南岸扣挂体系示意图

为简化计算模型，保证模型中扣索与拱肋节点处扣索伸长量一样，需要对扣索的弹性模量进行换算。由式

可知，伸长量与扣索长、扣索力、弹性模量和截面面积有关，当F 和A 确定后，索长与弹性模量成正比，通过该关系对模型中的扣索弹性模量进行换算。因为南岸和北岸对称，故表5-6只列出了南岸扣索换算值。

表5-6　南岸扣索弹性模量换算结果

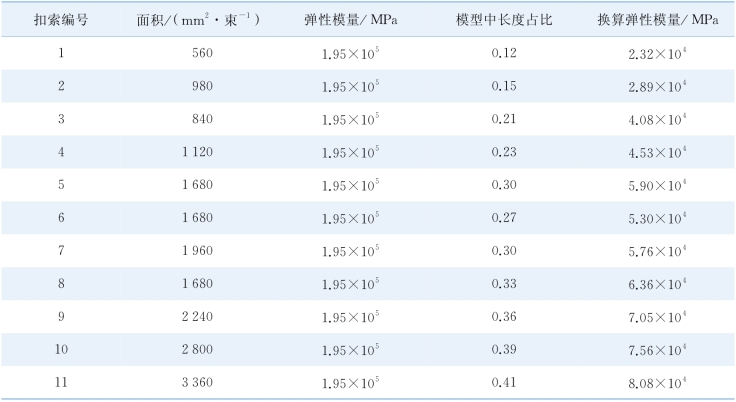
4）计算模型

按照设计图纸及施工组织方案对吊装拱肋建立空间有限元模型，如图5-24所示。

图5 24 平南三桥拱肋安装扣挂系统布置

5.3.3.3　计算方法

基于前面马滩红水河特大桥的研究表明，“过程最优，结果可控”斜拉扣挂一次张拉施工优化计算方法具有良好的计算效果。因此平南三桥拱圈扣索索力和线形的计算仍采用该计算方法。由于结构的对称性，这里取下游拱圈各控制点的线形和扣索力情况计算结果进行分析。

5.3.3.4　不同吊装顺序对比分析

整个吊装过程中采用对称吊装施工，第1～4节段吊装方式相同，这里主要讨论吊装第5节段至合龙节段安装过程中两种不同的吊装方案：

（1）方案1采用上下游各吊装一节段再吊装中间横联，即每吊装一节拱肋索鞍横移一次，直至合龙的吊装方式，整个吊装施工过程中扣索横移24次。

（2）方案2采用上下游各吊装两节段再连续吊装中间两段横联，直至拱圈合龙的吊装方式，即每吊装两节拱肋索鞍横移一次，整个吊装过程中索鞍横移15次。

方案1和方案2的吊装顺序如图5-25、图5-26所示。

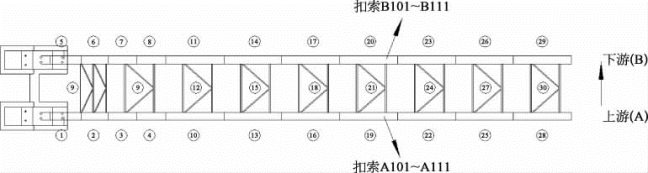
图5-25　吊装方案1（南半跨）

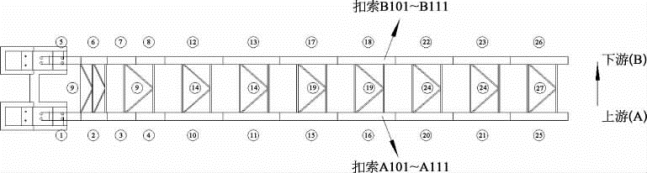
图5-26　吊装方案2（南半跨）

1）各扣索索力对比分析

经过计算发现，上游（A）和下游（B）扣索索力以及南岸（A101～A111、B101～B111）和北岸扣索索力（A201～A211、B201～B211）差别较小，因此这里取南岸上游扣索A101～A111进行对比分析，结果如图5-27所示。

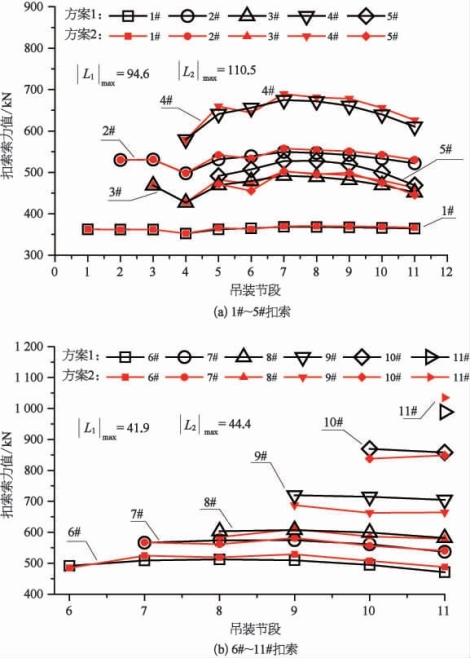
图5-27　各扣索索力变化（根据结构的扣索布置，1＃～4＃扣索为单束布置，5＃～11＃扣索为双束布置）

（1）各扣索索力均匀性。由图5-27可知，在整个吊装施工过程中，方案1和方案2各扣索索力变化的最大值分别为94.6 kN和110.5 kN，两者扣索索力差别很小且整个施工过程中扣索索力变化平缓，各扣索索力均匀性较好。

（2）最大扣索力及配索。由图5-28可知，在整个吊装施工过程中，相邻两扣索索力最大值偏差控制在200 kN以内，没有显著波动，各扣索索力均匀性较好。表5-7进一步表明方案1和方案2各扣索最大索力差别很小，拱圈所需扣索数量相同。

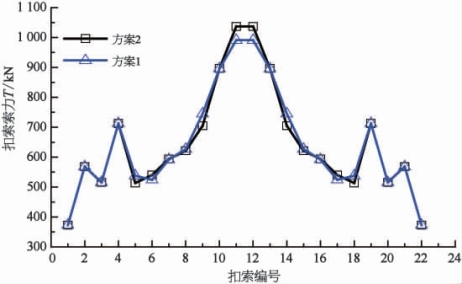
图5-28　各扣索最大索力

表5-7　半跨拱圈扣索配索　单位：根

2）应力对比分析

（1）弦杆应力。由图5-29可知，从安装第一个拱肋节段到安装最后一段横梁过程中，方案1和方案2的弦杆最大应力分别为46.9 MPa和46.1 MPa，最小应力分别为-119.9 MPa和-119.2 MPa，由此表明两种吊装方案在整个吊装施工过程中应力差别很小。

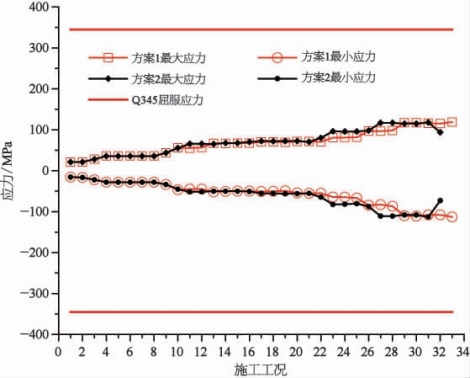
（2）腹杆应力。由图5-30可知，从安装第一个拱肋节段到安装最后一段横梁过程中，方案1和方案2的腹杆最大应力分别为119.0 MPa和118.1 MPa，最小应力分别为-113.0 MPa和-113.0 MPa，由此表明两种吊装方案在整个吊装施工过程中应力差别很小。

3）线形对比分析

（1）最大线形偏差。由图5-31可知，在整个吊装施工过程中，方案1和方案2预抬高值与目标线形的最大偏差分别为130 mm和125 mm，合龙松索后线形与目标线形偏差均为30 mm，小于规范要求的允许值L／3 000＝186.7 mm。由此表明两种吊装方案施工过程中线形与合龙松索后线形均较好，且方案1合龙松索后线形以及施工过程中的线形均与方案2相差很小。

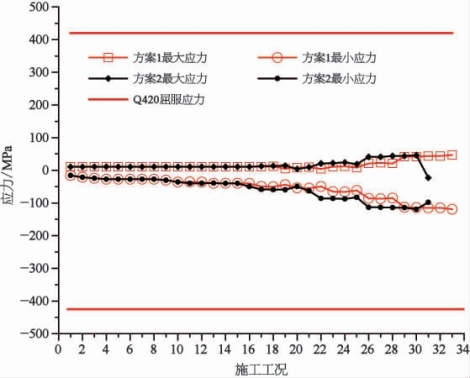
图5-29　各吊装施工过程中拱圈最大和最小应力

(www.xing528.com)

图5-30　各吊装施工过程中拱圈最大和最小应力

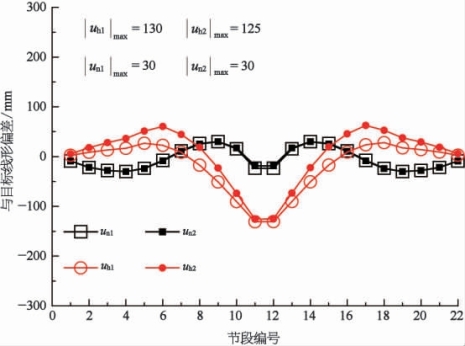
图5-31　各控制点线形偏差

uh1—方案1的预抬高值；uh2—方案2的预抬高值；un1—方案1的合龙松索后线形；un2—方案2的合龙松索后线形

（2）线形均匀性。为进一步研究各控制点在斜拉扣挂施工过程中线形的变化情况，取南岸上游控制点1＃～11＃（每个控制点对应一个扣索扣挂位置，控制点位置位于扣点位置）与目标线形的偏差情况进行对比分析，结果如图5-32所示。

由图5-32可知，在整个吊装施工过程中，方案1和方案2各控制点与目标线形的最大偏差分别为131.7 mm和137.8 mm（国标对合龙松索线形规定小于L／3 000＝186.7 mm，但未对施工过程中线形偏差进行规定），均与目标线形偏差较小，各控制点线形较为均匀。

4）白噪声试验对比分析

为模拟施工过程中的测量误差和拱圈制造误差对结构合龙线形的影响，对施工过程中安装预抬高值引入幅值为30 mm的白噪声，进行了200次试验分析，其结果如图5-33所示。

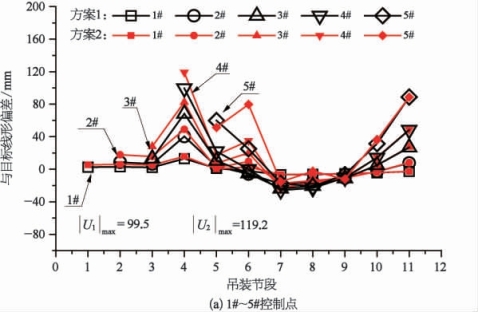
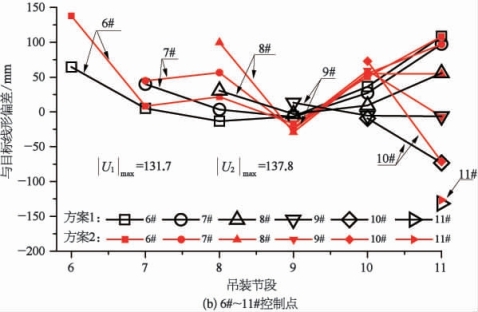
图5-32　各控制点与目标线形偏差

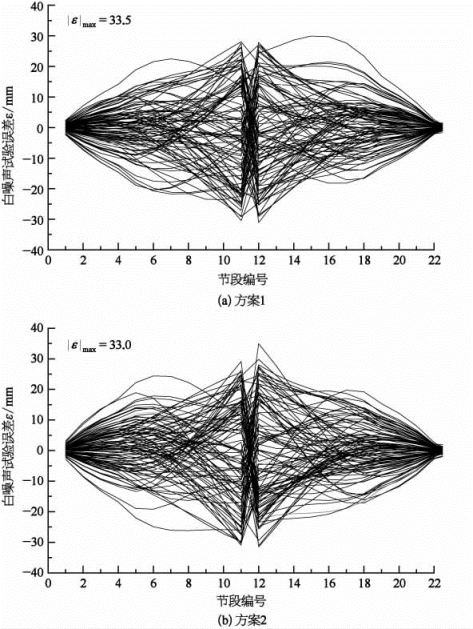
图5-33　各控制点线形偏差

由图5-33可知，方案1和方案2悬臂拼装施工过程中预抬高值误差30 mm，在松索成拱后分别被放大成为33.5 mm 和33.0 mm，两种方案相差很小，变化幅度均很小。由此表明方案1和方案2在施工过程中较小的线形偏差，在合龙松索后均不会被大幅度放大，施工线形精度良好。

以平南三桥为工程背景，采用“过程最优，结果可控”一次张拉施工优化方法对拱圈两种不同的吊装方案进行研究，从斜拉扣挂施工过程中的线形、索力以及白噪声试验等进行了计算和对比分析，结论如下：

（1）整个吊装施工过程中，方案1和方案2的扣索索力变化平缓，索力均匀性较好，两种方案各扣索配置数量相同；对两种不同吊装方案的弦管应力和腹杆应力进行对比分析，计算结果表明两种方案的最大／最小应力较钢材的屈服应力均有较大的安全富余。

（2）整个吊装施工过程中，方案1和方案2的施工过程线形与目标线形偏差控制均在140 mm范围内，合龙松索线形与目标线形偏差控制在30 mm范围内，远小于规范要求的允许值L／3 000＝186.7 mm。由此表明两种吊装方案施工过程中线形与合龙松索后线形均较好。

（3）通过白噪声试验研究表明，方案1和方案2悬臂拼装施工过程中预抬高值误差30 mm，在松索成拱后分别被放大成为33.5 mm和33.0 mm，两种方案相差很小，变化幅度均很小。由此表明方案1和方案2施工过程中较小的线形偏差，在合龙松索后不会被大幅度放大，施工线形精度良好。

（4）在整个吊装施工过程中，方案1和方案2的线形和扣索力相差较小，但是方案1所需的索鞍横移次数是24次，方案2横移次数为15次，因此建议采用方案2的吊装方式，以减小施工过程中的横移次数，提高施工效率和施工安全。

5.3.3.5　不同封拱脚方案对比分析

这里主要讨论三种不同的吊装方案：①两岸均在安装完第4段拱肋后封拱脚；②两岸均在吊装第6段拱肋后封拱脚；③两岸均在吊装第8段拱肋后封拱脚。

1）各扣索索力对比分析

（1）各扣索索力均匀性。由图5-34可知，在整个吊装施工过程中，三种封拱脚方案相邻两扣索索力在100 kN以内波动，各扣索索力变化平缓，均匀性较好。

（2）最大扣索力及配索。由图5-35可知，在整个吊装施工过程中，第6段封拱脚和第8段封拱脚相邻两扣索索力最大值偏差控制在200 kN以内，没有显著波动，各扣索索力均匀性较好。采用第4段封拱脚方案，5＃扣索和6＃扣索相差327 kN，存在较大波动性。表5-8进一步表明采用第4段封拱脚方案所需扣索数量略高于较其他两种封拱脚方案。

表5-8　半跨拱圈扣索配索　单位：根

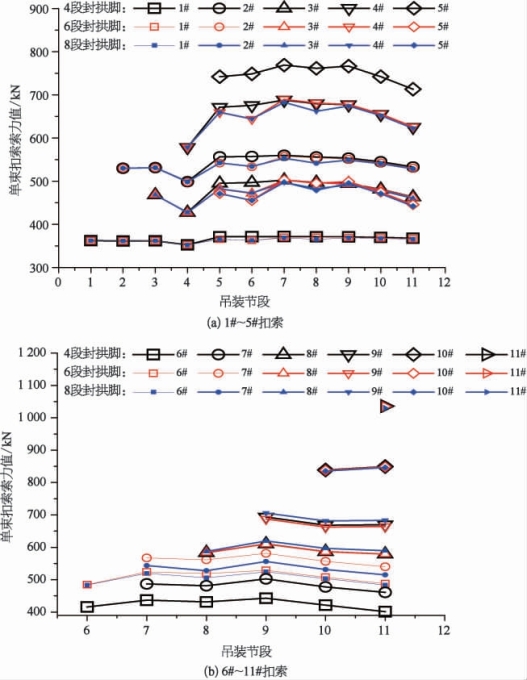
图5-34　各扣索索力变化情况（根据结构的扣索布置，1＃～4＃扣索为单束布置，5＃～11＃扣索为双束布置）

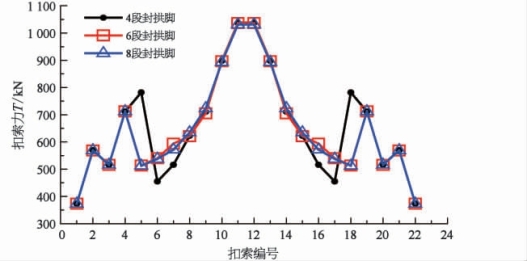
图5-35　各扣索最大索力

2）线形对比分析

（1）最大线形偏差。由图5-36可知，在整个吊装施工过程中，第4段封拱脚、第6段封拱脚和第8段封拱脚预抬高值与目标线形的最大偏差分别为160 mm、125 mm 和120 mm，合龙松索后线形与目标线形偏差均为30 mm，小于规范要求的允许值L／3 000＝186.7 mm。由此表明三种封拱脚方案施工过程中线形与合龙松索后线形均合理。此外，从线形精度考虑，第6段和第8段封拱脚方案的线形要优于第4段封拱脚方案。

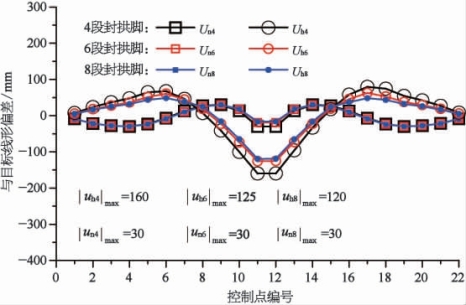
图5-36　各控制点线形偏差

（2）线形均匀性。为进一步研究各控制点在斜拉扣挂施工过程中线形的变化情况，取南岸上游控制点1＃～11＃（每个控制点对应一个扣索扣挂位置）与目标线形的偏差情况进行对比分析，结果如图5-37所示。

由图5-37可知，在整个吊装施工过程中，第4段封拱脚、第6段封拱脚和第8段封拱脚各控制点与目标线形的最大偏差分别为160.5 mm、137.8 mm和126.1 mm（国标对合龙松索线形规定小于L／3 000＝186.7 mm，但未对施工过程中线形偏差规定），均与目标线形偏差较小，各控制点线形较为均匀。

3）白噪声试验对比分析

为模拟施工过程中的测量误差和拱圈制造误差对结构合龙线形的影响，对施工过程中安装预抬高值引入幅值为30 mm的白噪声，进行了200次试验分析，其结果如图5-38所示。

由图5-38可知，第6段封拱脚方案和第8段封拱脚方案悬臂拼装施工过程中预抬高值误差30 mm，在松索成拱后分别被放大成为33.0 mm和32.2 mm，两种方案相差很小，变化幅度均很小。由此表明第6段封拱脚方案和第8段封拱脚方案施工过程中较小的线形偏差，在合龙松索后基本上不会被放大，施工线形精度良好。采用第4段封拱脚方案，对施工过程中安装预抬高值引入幅值为30 mm的白噪声，并进行了200次试验分析，在松索成拱后分别被放大成为44.0 mm，具有一定的施工风险。

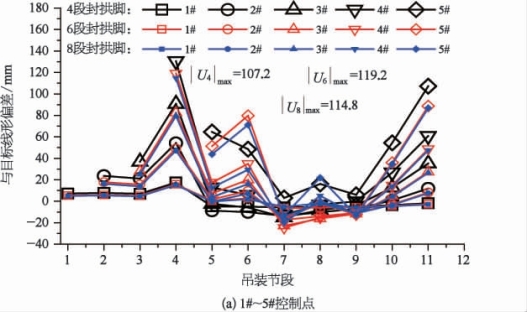
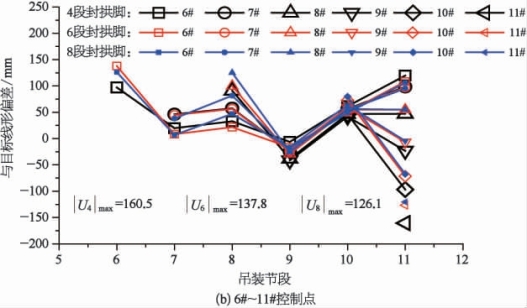
图5-37　各控制点与目标线形偏差

综上所述，可以得到以下结论：

（1）整个吊装施工过程中，三种封拱脚方案的扣索索力变化平缓，索力均匀性较好，第6段封拱脚和第8段封拱脚方案各扣索配置数量相同，略低于第4段封拱脚方案的扣索数量。

（2）整个吊装施工过程中，第6段封拱脚和第8段封拱脚方案施工过程线形与目标线形偏差控制均在140 mm范围内，第4段封拱脚方案施工过程线形与目标线形偏差达160.5 mm，三种封拱脚方案合龙松索线形与目标线形偏差控制在30 mm 范围内，远小于规范要求的允许值L／3 000＝186.7 mm。由此表明第6段封拱脚方案和第8段封拱脚方案优于第4段封拱脚方案。

（3）通过白噪声试验研究表明，第6段封拱脚方案和第8段封拱脚方案悬臂拼装施工过程中预抬高值误差30 mm，在松索成拱后分别被放大成为33.0 mm 和32.2 mm，两种方案相差很小，变化幅度均很小。采用第4段封拱脚方案，对施工过程中安装预抬高值引入幅值为30 mm 的白噪声，并进行了200次试验分析，在松索成拱后分别被放大成为44.0 mm，具有一定的施工风险。

（4）在整个吊装施工过程中，第4段封拱脚方案的线形、索力均匀性以及经济性均不及第6段封拱脚方案和第8段封拱脚方案，第6段封拱脚方案和第8段封拱脚方案的扣索数量、索力均匀性、线形精度均很接近。由于提前封拱脚有助于提高后续施工过程中的安全性，因此建议采用第6段封拱脚的施工方式。

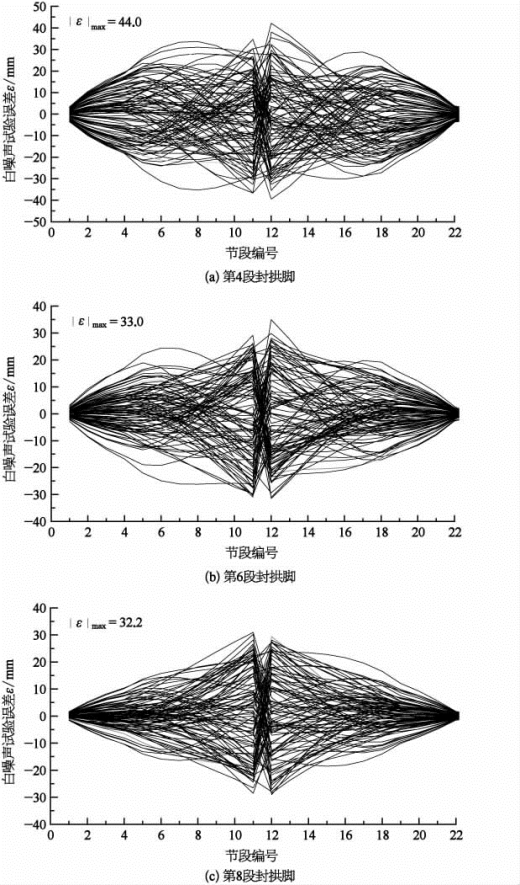
图5-38　各控制点线形偏差

以合龙松索后各节点的实际位移与目标线形位移差为约束条件、各吊装施工阶段的拱肋控制节点实际位移与目标位移差的平方和为优化目标函数，结合影响矩阵法建立“过程最优，结果可控”的CFST拱桥斜拉扣挂施工一次张拉最优化计算方法，有效克服了传统定长扣索法存在的约束条件多、索力均匀性有待解决的问题，应用于马滩红水河特大桥、六律大桥和平南三桥，具有良好的计算效果。

针对CFST拱桥的斜拉扣挂施工优化进行了分析，后续可结合影响矩阵原理进行拱桥吊杆无应力长度的计算分析。同时将进一步研究劲性骨架拱桥、斜拉桥等不同类型桥梁的施工优化方法，并将“过程最优，结果可控”推广应用于不同类型的桥梁施工中。

现有的规范仅对拱桥的合龙松索后的线形提出了限值要求，建议对施工过程中的线形偏差以及扣索均匀性提出相应的规范要求。

参考文献

［1］陈宝春，韦建刚，周俊，等.我国钢管混凝土拱桥应用现状与展望［J］.土木工程学报，2017，50（6）：50-61.

［2］郑皆连，徐风云，唐柏石.广西邕宁邕江大桥千斤顶斜拉扣挂悬拼架设钢骨拱桁架施工仿真计算方法［C］／／中国公路学会桥梁和结构工程学会1996桥梁学术讨论会论文集.南宁：中国公路学会，1996：214-228.

［3］周水兴，江礼忠，曾忠，等.拱桥节段施工斜拉扣挂索力仿真计算研究［J］.重庆交通大学学报（自然科学版），2000，19（3）：8-12.

［4］张建民，郑皆连，肖汝诚.钢管混凝土拱桥吊装过程的最优化计算分析［J］.中国公路学报，2005，18（2）：40-44.

［5］张治成，叶贵如，王云峰.大跨度拱桥拱肋线形调整中的扣索索力优化［J］.工程力学，2004，21（6）：187-192.

［6］张治成，叶贵如，陈衡治.大跨度钢管砼拱桥拱肋吊装中的扣索索力计算［J］.浙江大学学报（工学版），2004，38（5）：610-614.

［7］李传夫，李术才，魏建军，等.迭代优化算法在大跨拱桥线形控制中的应用［J］.山东大学学报（工学版），2008，38（3）：23-27.

［8］韩玉，秦大燕，郑健.CFST拱桥斜拉扣挂施工优化计算方法［J］.公路，2018，63（1）：100-104.