【摘要】：该优化模型以松索成拱后各拱段实际位移与目标位移差的平方和为优化目标函数，以各悬拼施工过程中的拱肋实际位移与目标位移差为约束条件，该方法为一次张拉方法，避免了应用正装法和倒拆法进行CFST拱桥斜拉扣挂施工优化计算时存在计算过程复杂、反复调索等缺点，进一步推动了CFST斜拉扣挂施工优化方法的发展。
式中 f（X）——待最小优化目标函数；
X、x——设计变量；
gi、hi、wi——状态变量，上划线和下划线分别表示上边界和下边界。
传统优化模型基于“过程可控，结果最优”的优化方法，以合龙松索后拱肋上各控制点位移与目标位移差的平方和为目标函数进行结构的最优化分析，其数学模型如下［5-6］：
设计变量：
目标函数：
约束条件：
式中 s——各组扣索索力组成的向量；
vj（s）——拱轴线上观测点的实际位移；(www.xing528.com)
——各观测点的目标位移；
L——扣索钢绞线的根数；
Np——单根钢绞线的屈服力；
k——安全系数；
v、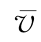
——各观测点的实际位移与目标位移的上、下限；
σj——结构各节点的应力；
σ——钢材的容许应力。
该优化模型以松索成拱后各拱段实际位移与目标位移差的平方和为优化目标函数，以各悬拼施工过程中的拱肋实际位移与目标位移差为约束条件，该方法为一次张拉方法，避免了应用正装法和倒拆法进行CFST拱桥斜拉扣挂施工优化计算时存在计算过程复杂、反复调索等缺点，进一步推动了CFST斜拉扣挂施工优化方法的发展。然而该方法采用“过程可控”的计算方法，导致在各吊装施工阶段中前后段拱肋实际位移与目标位移有一些较大偏差，需对钢材的应力和各扣索索力进行容许应力约束，进而造成约束条件多等问题。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
