500米级钢管混凝土拱桥的非线性承载能力影响

考虑到在实际工程条件中，不可避免地存在钢管初始应力和管内混凝土脱空的问题，钢管初始应力和管内混凝土脱空对钢管混凝土构件的刚度和极限承载力都有一定影响。因此通过理论计算和模型试验验证，在“统一理论”的基础上对其组合弹性模量以及应力-应变曲线进行0.85的折减，如图2-58所示。另外由于施工安装误差的存在，计算中还应引入结构“初始缺陷”对安装误差进行模拟分析。

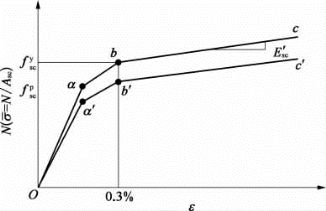
图2-58　修正后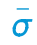ε关系曲线

图2-59　极限荷载特征点(www.xing528.com)

在稳定极限承载能力有限元分析中，极限荷载的确定方法不同，可能也会导致计算结果有所不同。在双重非线性分析时，可认为当材料的切线弹性模量少于或等于0时，结构被压溃，计算中断，此阶段的荷载作为极限荷载。在切线弹性模量少于或等于0的计算中断之前，可能曲线已经出现“拐点”，之后的曲线出现了平坦或反转段，甚至是曲线点徘徊，如图2-59所示。根据位移-荷载曲线，可根据以下几种情况来确定极限荷载（或荷载系数）：

（1）曲线转折点。当曲线经过转折点后，斜率大幅下降。曲线表明，当外荷载增加很少的情况下，拱的位移急剧增大，说明拱实际上已经被压溃。

（2）曲线反转点。当曲线经过反转点后，位移转向反方向。当外荷载作用下，拱上某点的位移沿一个方向移动，突然位移转向另一个方向，表明拱出现失稳。

（3）曲线徘徊点。当曲线经过徘徊点后，荷载增加微小，位移也增加微小，在一个很小的区段内，出现很多曲线点。说明拱已经不能继续承受更大的荷载，有限元程序反复在一个小区域内搜索有效解。