500米级钢管混凝土拱桥:徐变影响及承载能力

随着钢管混凝土拱桥技术发展和技术突破，世界最大跨径钢管混凝土拱桥——平南三桥已于2018年开工建设，该桥主拱主管直径为1.4 m，单根主拱管内混凝土用量为958 m3，管内混凝土的徐变影响已不容忽视。

目前，钢管混凝土的徐变计算方法主要有参数计算方法和分段常数计入法。

2.4.3.1　参数计算方法

四川省公路规划勘察设计研究院有限公司等单位通过对C60混凝土7 d、14 d、28 d、90 d四个龄期以及C50混凝土7 d、28 d、90 d三个龄期进行徐变、收缩试验，测得了相应的徐变收缩系数；另外还进行了节段模型的收缩徐变试验，得到了钢管混凝土的徐变规律以及应力重分布规律，提出了两种理论分析方法。

第一种理论分析方法以混凝土收缩徐变理论为基础，考虑钢管对混凝土收缩徐变的约束作用。其基本假定如下：①钢管与混凝土之间黏结良好，满足平截面假定；②假定模型为轴心受压构件，且压力恒定；③忽略收缩对徐变的影响。在假定条件下结合《公路钢筋混凝土及预应力混凝土桥涵设计规范》混凝土徐变系数的计算方法，通过考虑钢管对混凝土的约束作用，用考虑钢管约束的徐变调整系数来替代混凝土的徐变系数，计算钢管及混凝土的应力重分布规律。考虑钢管约束的混凝土徐变系数可按下列公式计算：

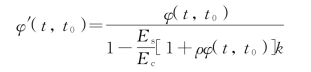
式中 t0——加载时的混凝土龄期（d）；

t——计算考虑时刻的混凝土龄期（d）；

φ（t，t0）——混凝土的徐变系数，可根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》附录F取值；

k——参数，；

ρ——参数，；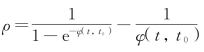

Es、Ec——钢管和混凝土材料弹性模量；

As、Ac——钢管和混凝土截面面积。

利用钢管约束的混凝土徐变系数，钢管与混凝土应力重分布值按下列公式计算：

压应力：

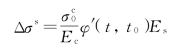
拉应力：

式中 Δσs——钢管的应力重分布值；

Δσc——混凝土的应力重分布值；

——加载时混凝土的应力值。(www.xing528.com)

对于轴心受压构件，第二种理论分析方法采用钢筋混凝土的分析思路来进行分析，将钢管等效为一根处于混凝土截面中心的钢筋，设混凝土的徐变（不受钢筋约束的情况下）为Δεc0。由于受到黏结的钢筋的约束，在钢筋水平处的混凝土实际徐变应变为Δεs，经过推导得到，钢管的重分布应力为

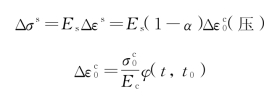
混凝土的重分布应力为

也可得到新的考虑钢管约束的徐变系数：

对于上述两种分析理论的比较，第一种在计算钢管的重分布应力比较准确，而第二种在计算钢管混凝土的混凝土徐变增量方面比较准确。就总体而言，第一种比第二种更精确，因此推荐采用第一种理论分析方法中的徐变系数进行分析。

2.4.3.2　分段常数计入法

通过大量模型试验，确定钢管混凝土徐变影响与轴压比的关系，提出钢管混凝土徐变折减系数。对于钢管混凝土轴压和e／rc≤0.3的偏压构件，将组合强度设计值乘以徐变折减系数Kc，见表2-31，表内中间值是采用插入法求得。

表2-31　徐变折减系数Kc值

当该表不能满足计算要求时，也可按下列公式计算：

当m≤0.4时，

Kc＝l2.5m（0.2m2-0.4m＋1）［1＋0.3m（1-n）］

当0.4＜m≤1.2时，

当m＞1.2时，

其中，l＝ξ0.05，m ＝λ／100，n＝（1＋e／r）-2，e为荷载偏心距，r＝D／2。

通过对钢管混凝土构件在不同含钢率、偏心率下的徐变特性研究表明：含钢率越大，构件徐变越小；外荷载越大，构件徐变越大；偏心率越大，构件徐变越大，且在小偏心受压状态下，徐变随偏心率增大的速率大于大偏心受压状态下徐变随偏心率增大的速率；在构件截面积相同的情况下，随着含钢率的增大，徐变引起的钢管与核心混凝土的应力重分布影响将有所减小。含钢率、偏心率对钢管混凝土构件的徐变影响在计算公式中同样有体现：对于参数计算方法，徐变系数计算中参数k即含钢率的体现，k越大，构件徐变越小；对于分段常数计入法，徐变折减系数计算公式中l、n也分别体现了含钢率和偏心率的影响。总的来说，在进行钢管混凝土结构设计时，从徐变引起的截面应力重分布方面考虑，应尽量增大构件含钢率。