网络计划资源，实现土木工程施工高效

所谓资源是指完成任务所需的人力、材料、机械设备和资金等的统称。在一定的时期内，某项建设项目所需的资源量基本上是不变的，一个部门的人力、物力和财力也是有一定限量的。因此，在编制网络计划时，必须对资源问题统筹安排。资源优化就是通过改变工作的开始时间，使资源按时间的分布符合优化的目标。

资源优化可以分为“资源有限、工期最短”和“工期固定、资源均衡”两类问题。

13.5.1 资源有限，工期最短

资源有限，工期最短的优化是指在资源有限的条件下，保证各项工作的每日资源需要量不变，寻求工期最短的施工计划的优化过程。

例如，某一网络计划如图13.5.1所示。箭线上的数字表示各活动的持续时间和所需要的人力资源。

图13.5.1

现每天需保证出勤人数不超过15人。若工作1—2、1—3和1—4都同时按最早可能开始时间开始工作，则1到3天每天需要劳动力20人，大于出勤限制人数15人。但如果将时差较大的工作1-3推迟到第6天以后开始，则每天最多需要劳动力14人。那么这个计划就可以实现了。

1. 优化方法

资源优化的过程实际上就是按照各项工作在网络计划中的重要程度，把有限的资源进行科学合理地分配的过程。因此，资源分配的先后顺序是资源优化的关键。

资源分配的顺序:

第一级: 关键工作。按每日资源需要量大小，从大到小依顺序供应资源。

第二级: 非关键工作。按总时差大小，从小到大依顺序供应资源。总时差相等时，以叠加量不超过且接近资源限额的工作优先供应资源。

第三级: 允许中断的工作。

2. 优化步骤

①将网络计划绘制成时标网络计划图，标明各项工作的每日资源需要量。

②计算出每个“时间单位”的资源需要量之和。

③从计划开始日期起，逐个检查每个“时间单位”的资源需用量是否超过资源限量。若整个工期内都能满足资源限额的要求，则完成优化。否则，进行第④步。

④找到首先出现超过资源限额的时段，按资源分配顺序对该时段内的各项工作重新进行资源分配，未分配到资源的工作向后移出该时段。其后的各时段因此发生资源需要量变化的，不予理会。

⑤绘制出调整后的时标网络计划图。

⑥重复②～⑤步，直至所有时段内的资源需要量都不超过资源限额，资源优化即告完成。

3. 优化实例

［例13.5.1］ 已知网络计划如图13.5.2所示。图13.5.2中箭线上方数据表示该工作每天需要的资源数量，箭线下方的数据表示该工作的持续时间 (天)。若资源限量为22，试求满足资源限量的最短工期。

图13.5.2 某项目的网络计划图

解 (1) 将网络计划绘制成时标网络计划图，如图13.5.3所示。

图13.5.3 某项目时标网络计划图

(2) 对时标网络计划进行优化。

第一步: 根据图13.5.3中数据，计算每日所需资源量，如表13.5.1所示。

从计划开始日期起，逐个检查每天的资源数量。找到首先出现超过资源限额的时段，即第1、2天。按资源分配顺序对该时段内的各项工作进行资源分配。

表13.5.1 每日资源数量表

该时段内共有3项工作，即1—3、1—2和1—4工作。根据分配原则，1—3工作为关键工作，首先分配资源10个单位。1—2、1—4工作均为非关键工作，比较总时差大小。1—2工作的总时差为2天，大于1—4工作的总时差1天，先分配1—4工作资源12个单位。1—3工作和1—4工作的资源之和为22个单位，满足资源限量22个单位。把1-2工作向后移2天，移出该时段，形成新的时标网络计划，如图13.5.4所示。

图13.5.4

第二步: 根据图13.5.4中的数据，计算每日所需资源量，如表13.5.2所示。

表13.5.2 每日资源数量表

从计划开始日期起，逐个检查每天的资源数量。找到首先出现超过资源限额的时段，即第3、4天。按资源分配顺序对该时段内的各项工作进行资源分配。

该时段共有4项工作，即1—2、1—3、4—6和4—7工作。其中1—3工作为关键工作，1—2工作的总时差已耗尽，首先分配资源给1—3工作和1—2工作，资源之和为16个单位。此时，资源无论分配给4—6工作或4—7工作都会超过资源限量，必须把4—6工作和4—7工作后移2天。由于4—6工作的总时差只有1天，关键工作6—8工作是4—6工作的紧后工作，因此要保证资源限量，6—8工作也必须后移1天。形成新的时标网络计划，如图13.5.5所示。

第三步: 根据图13.5.5中的数据，计算每日所需资源量，如表13.5.3所示。

图13.5.5

表13.5.3 每日资源数量表

从计划开始日期起，逐个检查每天的资源数量。找到首先出现超过资源限额的时段，即第6天、第7天。按资源分配顺序对该时段内的各项工作进行资源分配。

该时段共有4项工作，即2—5、3—6、4—6和4—7工作。关键工作3—6首先分配资源2个单位。按照总时差由小到大的顺序依次给4—6、2—5和4—7工作试配资源。由于资源限量的控制，4—7工作要移出该时段，后移3天。形成新的时标网络计划，如图13.5.6所示。

图13.5.6

第四步: 根据图13.5.6中的数据，计算每日所需资源量，如表13.5.4所示。

表13.5.4 每日资源数量表

从计划开始日期起，逐个检查每天的资源数量，整个网络计划的资源用量都控制在资源限量以内。图13.5.6所示时标网络计划就是最优解。

13.5.2 工期固定，资源均衡

1. 基本概念和指标

工期固定，资源均衡的优化是指在工期保持不变的条件下，使资源需要量尽可能均衡的优化过程。也就是在资源需要量曲线上尽可能不出现短期高峰或长期低谷情况，力求使每天资源需要量接近于平均值。

衡量资源是否均衡的指标通常有三个，即:

(1) 资源不均衡系数K

式中: Rmax——最高峰日期的资源需要量;

Rm——每天平均资源需要量。

显然，资源不均衡系数K愈小，资源均衡性愈好。

(2) 资源极差值ΔR

式中: R (t) ——第t天的资源需要量。

同样，资源极差值愈小，资源均衡性愈好。

(3) 资源均方差σ2

同样，资源均方差愈小，资源均衡性愈好。

2. 优化的方法和步骤

(1) 优化方法

现说明用资源均方差σ2衡量资源均衡性的方法。资源均方差是用以描述每天的资源需要量对资源需要量的平均值的离散程度。这种方法主要是利用自由时差对网络计划进行改进，使资源需求量曲线的均方差值减到最小，从而达到资源均衡的目标。(www.xing528.com)

资源均方差的表达式可以展开为

由于上式中T和Rm为常数，只要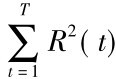最小就可以使资源均方差最小，即

假定在网络计划中，有某一非关键工作i-j开始于第k天，结束于第l-1天，每天的资源需要量为ri-j，则这项工作它向后(右) 移动1天时，资源均方差之和的增量为

化简后得

当Rl- (Rk-ri-j) 为非正值时，意味着工作i-j右移1天能使资源均方差之和减小或保持不变，那么就将这项工作向右移1天。

在新的资源曲线上按上述同样的方法继续考虑工作i-j是否还能再右移1天，如果能再右移1天，那么就再右移1天，直至不能移动为止。

如果Rl- (Rk-ri-j) 为正值，表示工作i-j不能向右移1天，那么考虑能否(在总时差许可的范围内) 向右移2天。计算［Rl- (Rk-ri-j)］+ ［Rl+1- (Rk+1-ri-j)］的值，若这个值为非正值，那么工作i-j就右移2天，进一步考虑工作i-j能否 (在总时差许可的范围内) 向右移3天的问题。

如果工作i-j的右移时间确定以后，再按上述方法考虑其他的工作移动。

(2) 优化步骤

①将网络计划改成时标网络计划。

②计算“单位时间”资源需要量之和。

③按节点最早开始时间的后先顺序，自右向左地进行调整。

若节点n为最右 (后) 的一个节点，则首先对以节点n为结束点的工作进行调整。在以节点n为结束点的工作中，首先调整最早开始时间最迟的工作。最早开始时间相同的工作中，以自由时差较小的工作先行调整。当它们的时差相同时，以资源需要量大的先行调整。

④绘制出调整后的时标网络图，重新计算“单位时间”资源需要量之和。按上述顺序对其他工作进行调整。

⑤按节点最早开始时间的后先顺序，自右向左继续调整。

为使资源均方差值进一步减小，重复③～⑤步，进行第二次优化。反复循环直至所有工作都不能再优化为止。

3. 优化示例

［例13.5.2］现仍以图13.5.2为例，说明工期固定，资源均衡的优化步骤。

解: (1) 将网络计划改成时标网络计划。如图13.5.7所示。

根据图13.5.7中的数据，计算每日所需资源量，如表13.5.5所示。

表13.5.5 每日资源数量表

图13.5.7

假设资源的供应没有限制，则由表13.5.5可知，每天资源最大需要量Rmax=33个单位，每天平均需要量为

Rm= (28×2+32×1+33×1+25×1+16×1+19×1+17×3+12×2+10×1+6×4) ÷17=17.06

资源需要量不均衡系数为

(2) 对时标网络计划进行优化。

为了使计划的总持续时间满足工期不变的条件，因此在以下调整过程中不考虑位于关键线路上的工作，即工作1—3、3—6、6—8和8—9不移动。

第一次调整:

①对以节点9为结束点的7—9工作进行调整，7—9工作自由时差为4天。

由于R14- (R7-r7-9) =6- (19-4) =-9＜0 可以右移1天 ES7-9=7

又因R15- (R8-r7-9) =6- (17-4) =-7＜0 可以再右移1天 ES7-9=8

R16- (R9-r7-9) =6- (17-4) =-7＜0 可以再右移1天 ES7-9=9

R17- (R10-r7-9) =6- (17-4) =-7＜0 可以再右移1天 ES7-9=10

7—9工作共向后移动4天，已移至最右端，不能再移。

绘制出调整后的时标网络计划图，如图13.5.8所示。根据图13.5.8中的数据，计算每日所需资源量，如表13.5.6所示。

图13.5.8

表13.5.6 每日资源数量表

②对以节点8为结束点的工作5—8进行调整，5—8工作自由时差有2天。

由于R11- (R8-r5-8) =12- (13-5) =4＞0不能右移。

又因R12- (R9-r5-8) =12- (13-5) =4＞0不能右移。

③对以节点7为结束点的工作4—7进行调整，4—7工作自由时差有4天。

R7- (R3-r4-7) =15- (32-7) =-10＜0 可以右移1天　ES4-7=3

R8- (R4-r4-7) =13- (33-7) =-13＜0 可以再右移1天　ES4-7=4

R9- (R5-r4-7) =13- (25-7) =-5＜0 可以再右移1天　ES4-7=5

R10- (R6-r4-7) =13- (16-7) =4＞0 不能右移。

绘制出调整后的时标网络计划，如图13.5.9所示。根据图13.5.9中数据，计算每日所需资源量，如表13.5.7所示。

表13.5.7 每日资源数量表

④对以节点6为结束点的工作4—6进行调整，4—6工作自由时差有1天。

R6- (R3-r4-6) =16- (25-9) =0

可以不右移。

⑤由于以节点5、4、3、2为结束点的工作的自由时差均为0，故不可右移。自此，第一次调整结束。

图13.5.9

按照上述方法自右向左再进行第二、三、……次调整，直至所有工作都不能移动。调整过程由读者自行完成。最后结果如图13.5.10所示。

图13.5.10

根据图13.5.10中的数据，计算每日所需资源量，如表13.5.8所示。

表13.5.8 每日资源数量表

由表13.5.8可知，每天资源最大需要量Rmax=25个单位，资源需要量不均衡系数为

不均衡系数K比未优化前的1.93改善了许多。