测量员上岗必读：高效使用地形图方法

（一）在图上确定某点坐标

在大比例尺地形图上画有10cm×10cm的坐标方格网，并在图廓西、南边上注有方格的纵横坐标值，如图8-3所示，要求P点的平面直角坐标（x_p，y_p），可先将P点所在坐标方格网用直线连接，得正方形abcd，过P点分别作平行于x轴和y轴的两条直线mn和kl，然后用分规截取ak和an的图上长度，再依比例尺算出ak和an的实地长度值。

已知ak=520m，an=260m，则P点的坐标为：

x_p=x_a+ak=（2200+520）m=2720m

y_p=y_a+an=（1700+260）m=1960m

为了检核，还应量出dk和bn的长度。如果考虑到图纸伸缩的影响，可按内插法计算：

x_p=x_a+（10/ad）×ak

y_p=y_a+（10/ad）×an

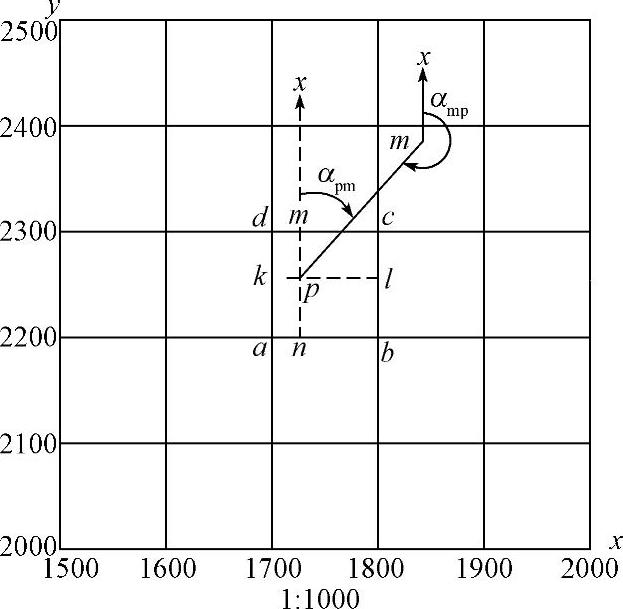
图8-3 地形图基本应用示意图（一）

（二）在图上确定某点高程

地形图上任一点的高程，可以根据等高线及高程标记来确定，如图8-4所示，如果某点A正好在等高线上，则其高程与所在的等高线高程相同，即H_A=104.0m。如果所求点不在等高线上，如图8-4中的H点，而位于106m和108m两条等高线之间，则可过H点作一条大致垂直于相邻等高线的线段mn，量取mn的长度，再量取mB的长度，若分别为9.5mm和3mm，已知等高距h=2m，则B点的高程H_B可按比例内插求得：

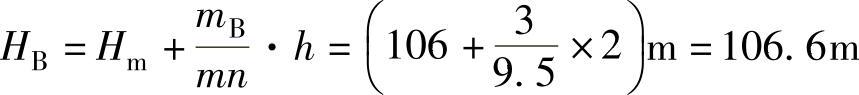
在图上求某点的高程时，通常可以根据相邻两等高线的高程目估确定。例如图8-4中m_B约为mn的3/10，故B点高程可估计为106.6m。因为，GB 50026—2007《工程测量规范》中规定，在平坦地区等高线的高程中误差不应超过1/3等高距；丘陵地区不应超过1/2等高距；山地不应超过2/3等高距，高山地不应超过一个等高距。也就是说，如果等高距为1m，则平坦地区等高线本身的高程误差允许到0.3m，丘陵地区为0.5m，山地为0.67m，高山地可达1m。显然，所求高程精度低于等高线本身的精度，而目估误差与此相比，是微不足道的。所以，用目估确定点的高程是可行的。

（三）在图上确定两点间距离

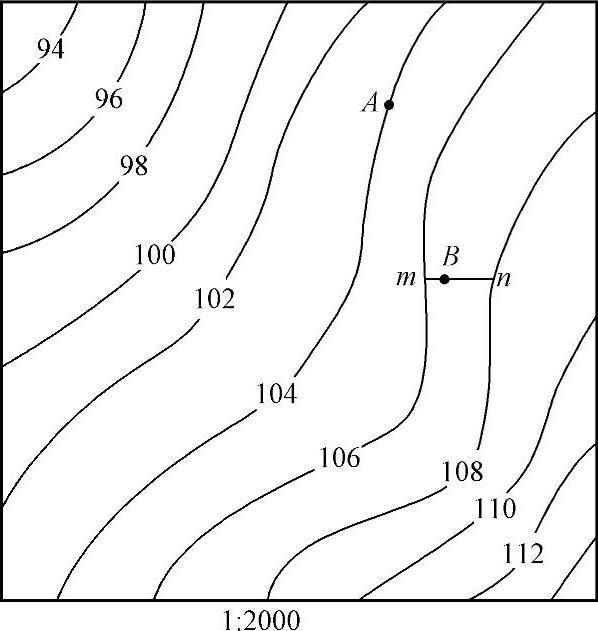
图8-4 地形图基本应用示意图（二）

1.直接测量

用卡规在图上直接卡出线段长度，再与图示比例尺比量，即可得其水平距离。也可以用毫米尺量取图上长度并按比例尺换算为水平距离，但后者会受图纸伸缩的影响，误差相应较大。但图纸上绘有图示比例尺时，用此方法较为理想。

2.根据直线两端点的坐标计算水平距离

为了消除图纸变形和量测误差的影响，尤其当距离较长时，可用两点的坐标计算距离，以提高精度。如图8-4所示，欲求直线mn的水平距离，首先求出两点的坐标值x_m、y_m和x_n、y_n，然后按下式计算水平距离：(www.xing528.com)

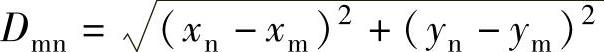
（四）在图上确定某直线坐标方位角

如图8-4所示，欲求图上直线mn的坐标方位角，有下列两种方法。

1.图解法

当精度要求不高时，可用图解法用量角器在图上直接量取坐标方位角。如图所示，先过m、n两点分别精确地作坐标方格网纵线的平行线，然后用量角器的中心分别对中m、n两点量测直线mn的坐标方位角α′_mn和nm的坐标方位角α′_nm。同一直线的正、反坐标方位角之差为180°，所以可按下式计算：

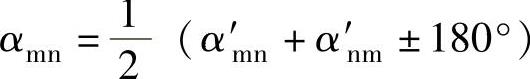
上述方法中，通过量测其正、反坐标方位角取平均值是为了减小量测误差，提高量测精度。

2.解析法

先求出m、n两点的坐标，然后再按下式计算直线mn的坐标方位角：

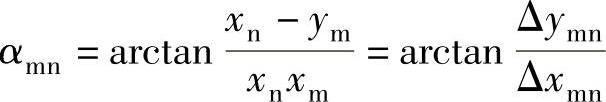
当直线较长时，解析法可取得较好的结果。

（五）在图上确定直线坡度

在图上求得直线的长度以及两端点的高程后，可按下式计算该直线的平均坡度i。

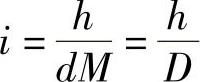
式中 d——图上量得的长度；

h——直线两端点的高差；

M——地形图比例尺分母；

D——该直线的实地水平距离。

坡度通常用千分率或百分率表示，“+”为上坡，“-”为下坡。