高速铁路中等压缩性土地基工程研究

早在20世纪30年代就有学者开始对非饱和土进行研究，但是由于难度较大，进展非常缓慢。直到50年代后期，解释非饱和土若干性状的概念才在英国帝国大学进行的研究中建立起来（Bishop，1959年）。20世纪50年代末到70年代中期，非饱和土研究取得了一些非常重要的成果，Bishop有效应力公式（1960年）和Fredlund双应力变量理论（1978年）都是在这一时期提出的，这个阶段的研究特点是将饱和土力学有关理论借用到非饱和土研究中。20世纪80年代后期，对非饱和土的研究更加深入，Alonso（1990年）提出了非饱和土的弹塑性本构模型。然而受吸力量测技术的影响，直到20世纪90年代才系统地建立起非饱和土固结理论。我国对非饱和土的研究始于20世纪60年代。俞培基、包承纲（1979年，1998年）等按照土体内部水气结构特征对非饱和土进行重新分类。1995年，殷宗泽等设计了我国首台用于研究非饱和土强度和变形的非饱和土三轴仪。随后，国内很多学者通过对非饱和土的研究提出了广义吸力的概念，初步建立了适用于非饱和土的广义固结理论、统一变形理论。

在过去的半个世纪里对非饱和土的理论研究得到了长足发展，各种本构理论、强度理论、固结理论被相继提出，其中的部分理论已经逐渐成熟起来，并且在岩土工程的各个领域得到广泛应用。但是由于试验条件限制，国内外对非饱和土的研究还处于起步阶段，尚未形成完整的理论体系，在工程实际应用中的难度很大。尤其是非饱和土固结理论，仅一维固结问题涉及的变量就达十几个之多。如何确定参数，简化模型，把非饱和土理论实用化，已经成为非饱和土研究所要面临的最突出的问题之一。

1.2.1.1　非饱和土的分类方法研究概况

目前，非饱和土的分类有很多种，其中具有代表性有以下几种：

1.俞培基等的分类方法

俞培基（1965年）等通过高柱法试验、渗透试验和击实试验研究了非饱和土的基本水-气形态。通过几项土工试验的成果，按照孔隙中水相和气相的存在形态，将非饱和土划分为3种类型：① 气封闭系统，孔隙中气相被孔隙水所分隔、孤立，以气泡形式存在，此时孔隙水相互贯通并与大气连通；② 双开敞系统，孔隙水和孔隙气都是连通的，并且有各自的通道与土体表面相连；③ 水封闭系统，此时孔隙气是连通的，而孔隙水被土粒和气相分隔，处于封闭状态。

俞培基的试验研究表明，气封闭系统和双开敞系统的界限饱和度一般为80%～87%，进入水封闭系统的临界饱和度一般为20%～25%。尽管如此，相邻系统的界限饱和度并不存在截然的分界线，受土质情况、取样过程、试验方法等因素影响，实际上是一个变化范围。就力学性质而言，水封闭和双开敞系统的差别不是很大，与气封闭系统相比就有显著不同，后者渗透系数小，气压消散缓慢。

2.包承纲的分类方法

包承纲（1979年，1998年）依据气相形态将非饱和土分为4种类型：气相完全连通、气相部分连通、气相内部连通和气相完全封闭。各类非饱和土的极限饱和度、液相形态、气相形态如表1.2-1所示。

表1.2-1　包承纲依据气相形态的非饱和土分类方法

3.Barden的分类方法

Barden（1965年）按照非饱和土的饱和度和干湿程度将非饱和土划分为5种，如表1.2-2所示。Barden认为通常研究的非饱和土饱和度介于20%～90%，Sr<20%和 Sr>90%的土属于是两种特殊的非饱和土，分别称为干土和饱和土。干土的强度变形特性与饱和度没有关系，而饱和土的研究相对成熟。

表1.2-2　Barden依据气相形态的非饱和土分类方法

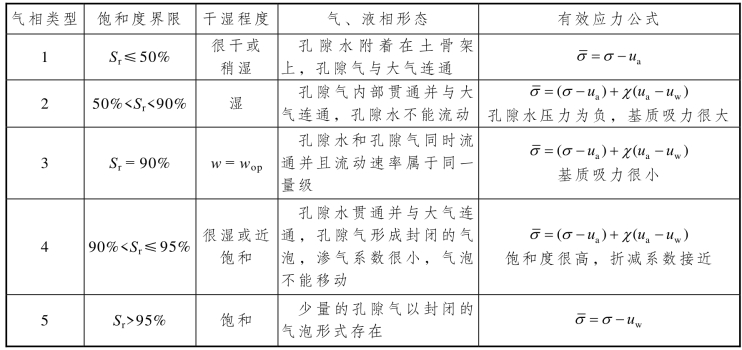
注：wop为最优含水量。

4.其他分类方法

蒋彭年在俞培基分类方法的基础上提出将含分散气泡的非饱和土（气封闭）分为两类：一是分散气泡远远小于土颗粒的高饱和土，其中水气交界面的曲率半径等于气泡的半径，曲率半径控制了气压力和水压力的差值；二是气泡远远大于土粒的非饱和土，其中的大气泡周界处为许多小气泡包围，各个土粒间跨界的许多小弯液面形成了水气交界面。

为了进一步研究不同饱和状态下的吸力效应，有关学者对非饱和土分类方法进行了补充。非饱和土的一个主要特征是孔隙水具有明显的表面现象。对于水封闭下的非饱和土，弯液面全部在土颗粒表面搭接，表面张力全部作用于土颗粒。对于气封闭的非饱和土，在气泡边界上，表面张力与液压平衡，对土颗粒没有直接的作用，即表面张力对颗粒的作用完全表现为液压。较为复杂的情况是双开敞非饱和土。考虑到表面张力对土颗粒的作用，研究认为可以将双开敞非饱和土按照弯液面是否与颗粒表面搭接进一步地细分为两种：

（1）单个土颗粒周围的弯液面部分与颗粒自身的表面搭接，其余部分则与其他颗粒周围的弯液面相连，不同颗粒周围的弯液面之间可以传递表面张力，这里将处于这种状态的非饱和土称为搭接双开敞非饱和土。

（2）当饱和度进一步增大时，弯液面完全不与颗粒表面搭接，此时各颗粒四周的表面张力在孔隙水表面传递，表面张力对颗粒不产生直接的作用，这里将处于这种状态的非饱和土称为不搭接双开敞非饱和土。

通过以上分类可以看出，正是由于非饱和土的内部结构特征对土体的工程力学特性起着至关重要的作用，非饱和土的分类方法都是从土体内部气相和液相的存在形式入手。Barden的分类方法将饱和度—气、液相形态—力学特性联系起来，侧重饱和度对土体力学特性的影响，划分细致，概念清晰，但是在实际应用上有一定的难度。包承纲和俞培基的分类方法着重于物理性质的本质，并且简单适用。

1.2.1.2　非饱和土水土特性研究概况

吸力是非饱和土研究中的核心内容。非饱和土的吸力是由渗透吸力和基质吸力两部分组成的，其中基质吸力为土中水自由能的毛细部分，是由非饱和土中收缩膜分子间的作用力引起的，通常采用孔隙气压力（ua）和孔隙水压力（uw）的差值来定义，如式（1.2-1）所示：

式中　Ts——水的表面张力；

　　　Rs——弯液面的半径。

基质吸力源于表面张力，通常和水的表面张力引起的毛细作用联系在一起。在毛细作用下形成的弯液面具有弹性薄膜的性状，而基质吸力正是为了平衡弯液面所产生的表面张力。从式（1.2-1）可以看出，基质吸力的大小取决于弯液面的曲率半径，也就是说基质吸力大小与非饱和土的内部结构形态有着必然联系。

Bishop和Fredlund在各自的非饱和土强度理论中都引入了吸力，Bishop将吸力看成是有效应力的一部分，Fredlund双应力理论将吸力作为独立的变量。如同荷载一样，吸力与变形本身就是一种应力-应变关系。引入吸力使得非饱和土本构关系变得更加复杂，但计算结果更加精确。因此，绝大多数本构模型都引入了吸力。

目前，非饱和土理论无法直接计算得到吸力值，必须依赖于试验。为了获得准确的吸力值，轴平移技术在试验过程中被广泛采用，但是由于非饱和土试验设备昂贵、试验时间长、试验成本高等问题，吸力的量测一直是困扰非饱和土研究的难点问题。

水土特征曲线的概念最早起源于土壤学。1939年，在威尔士召开的国际土壤学科学会第一届委员会上，Childs（1940年）提出将含水量和毛细势（吸力）之间的连续函数定义为水分特征曲线。早期的水土特征曲线研究是将其概念性地理解为土中水的体积或质量与水相能量之间的关系，着重对土的吸力变化、持水特性及水分运动特征进行研究。后来随着非饱和土理论的发展，逐渐将水土特征曲线的概念引入其中。

水土特征曲线是指基质吸力和重量（体积）含水量的关系曲线。典型的非饱和土水土特征曲线如图1.2-1所示，可以分为3个阶段：① 边界效应阶段；② 转化阶段；③ 残余阶段。图中对应的两个特征点A、B分别对应非饱和土的进气值和残余含水量，其中进气值是空气开始进入土体的临界吸力。从图中可以看出，当含水量低于残余含水量或高于进气值对应的含水量时，含水量的微小变化都会造成基质吸力的大幅增加。

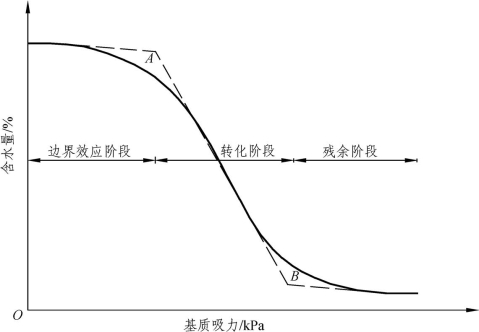
图1.2-1　典型非饱和土水土特征曲线

1.水土特征曲线的影响因素

事实上，水土特征曲线包含了孔隙结构、土颗粒排列方式、孔隙水分布形式等多种土体结构信息。因此，水土特征曲线的影响因素非常复杂，归纳起来主要有以下几个方面：

（1）土的矿物成分，包括土颗粒矿物成分和孔隙中的可溶盐。在相同饱和度下，土中黏粒含量越高，比表面积越大，毛细现象越显著，基质吸力就会越大。工程力学特性表现为良好的亲水力，对于具有较强亲水力的矿物组成的土，吸力也必然很大，反映在水土特征曲线上，则为残余含水量较大。

（2）孔隙结构，包括孔隙尺寸及组成结构。孔隙结构影响到水土作用面积和收缩膜的弯曲程度，后者直接决定了吸力的大小。孔隙结构的差异与土的持水性有密切联系，孔径大小导致土体内部不同的连通方式。土粒级配均匀的土，孔径小，则进水和脱水比大孔径困难，土的持水性弱，进气值低，脱水后的残余含水量高。

（3）应力状态，对水土特征曲线的影响包含内容更加广泛，比如应力历史、原状土扰动、路基填筑等人为因素都会造成土体结构的根本性变化，影响土的持水能力，改变水土特征曲线的形状。对于相同土质的非饱和土，在不同饱和度下，原状土的吸力较扰动土大。

（4）温度，对吸力的影响主要是水的黏滞度和表面张力引起的。温度升高，吸力下降，尤其是低饱和度和黏粒含量较高的土质表现最为显著。

水土特征曲线反映了吸力随含水量的变化关系，而对吸力的研究源于毛细现象中的表面张力，考虑表面张力的大小就不能忽略收缩膜的性质，收缩膜的形状、弯曲程度、接触角都依赖于土自身的物理力学特性。因此，在以上几个影响因素中，以矿物成分和孔隙结构对水土特征曲线的形状影响最为显著。

2.水土特征曲线的数学模型

水土特征曲线对研究非饱和土的强度、变形有非常重要的作用，为了能够更好地描述水土特征曲线的形状，分析非饱和土的内部结构，掌握其工程力学特性，研究人员逐渐建立其各类数学模型，典型数学模型有以下4种：

（1）以对数函数的幂函数形式表达的数学模型。

Fredlund等通过对土体孔径分布曲线的研究，用统计分析理论推导出适用于全吸力范围的通用水土特征曲线表达式：

其中，

式中　a，b，c——拟合参数；

　　　a——进气值函数的土性参数；

　　　b——当基质吸力超过土的进气值时，土中水流出率的函数的土性参数；

　　　c——残余含水量的土性参数；

　　　e——孔隙比；

　　　ψ——基质吸力；

　　　ψr——残余含水量θr对应的基质吸力；

　　　θ——体积含水量；

　　　θs——饱和体积含水量。

式（1.2-2）中体积含水量的取值范围是θ∈[0，θs]，基质吸力ψ的取值范围为ψ∈[0，ψmax]，ψmax 是土体积含水量θ=0时所到达的最大基质吸力。由此可见，全吸力范围是指0～106 kPa，通过对不同种类的土进行试验发现，对应零含水量的基质吸力基本一致，约为106 kPa。虽然Fredlund推导出的水土特征曲线表达式适用于所有土质全吸力的范围，但是模型很复杂，给实际应用带来诸多不便。

（2）幂函数模型。(www.xing528.com)

Van Genuchten通过对水土特征曲线的研究，得出非饱和土含水量和基质吸力间的幂函数的关系式：

式中　a——进气值函数的土性参数；

　　　b——当基质吸力超过土的进气值时，土中水流出率的函数的土性参数（体积含水量的取值范围是θ∈（θr，θs]）；

　　　ψ——基质吸力，其取值范围为：ψ∈[0，ψr）。

该公式适用于高于残余含水量范围的水土特征曲线。

（3）分形模型。

土水特征曲线的分形模型基于土体质量分布具有分形特征，以及孔隙数目与孔径之间的具有分形关系的认识。依据分形孔隙数目与孔径之间关系和Youg-Laplace方程得到分形模型的通用表达式：

式中　Dv——孔隙体积分布的分维值，Dv<3；

　　　ψb——进气值对应的基质吸力。

公式（1.2-4）中，体积含水量的取值范围为θ∈（θr，θs]，基质吸力ψ的取值范围为ψ∈[ψb，ψr），该式适用于基质吸力变化范围为ψ∈[ψb，ψr）的水土特征曲线，其实分形模型也是幂函数模型的一种。

（4）对数函数模型。

包承纲等结合气相形态将非饱和土划分为4种形态，提出水土特征曲线的进气值与气相完全封闭和气相内部连通的分界点相对应，残余含水量与气相内部连通和气相完全连通的分界点对应。参照Fredlund的水土曲线公式，发现曲线在进气值和残余含水量两个特征点之间近乎为一条直线，于是建议采用对数方程在表征水土特征曲线，并将其简化如下：

式（1.2-5）中体积含水量的取值范围为θ∈[θr，θs]，基质吸力ψ的取值范围为ψ∈[ψb，ψr]，该式适用于基质吸力在ψ∈[ψb，ψr]的范围内变化，较前面几种数学模型，对数模型更加简单适用。

1.2.1.3　非饱和土强度特性

已有的研究表明，非饱和土的强度随着基质吸力的增加而增大，这是由于吸力增加了土颗粒之间的抗滑阻力。与饱和土抗剪强度不同，非饱和土的抗剪强度由3个部分组成：① 由凝聚力产生的强度；② 土受外部有效应力作用而产生的摩擦强度；③ 由基质吸力产生的强度可称为吸附强度。通常将非饱和土强度看成是饱和土的强度和吸附强度之和。

目前，研究非饱和土强度的公式非常多，国内的学者如卢肇均（1997年）、徐永福等都对此做过研究，但是最具有代表性的非饱和土的强度公式有两类：Bishop公式和Fredlund公式。Bishop根据太沙基有效应力原理和实验研究，将有效应力公式σ′=（σ-ua）+χ（ua-uw）带入莫尔-库仑准则得到以下非饱和土抗剪强度公式：

式中　c′、φ′——饱和土有效黏聚力和有效内摩擦角；

　　　ua、uw——孔隙气压力和孔隙水压力；

　　　χ ——与饱和度有关的参数，非饱和土取0～1.0，饱和土取1.0，干土取0。

Bishop（1960年）在文献中给出了用三轴实验结果确定有效应力参数χ 的方法，并于1963年给出了根据4种不同的压实黏土样品剪切实验得到的参数χ 与饱和度的关系，继而又有很多学者研究了不同类型土的有效应力参数χ 的确定。研究表明，有效应力参数χ 与非饱和土的结构、应力历史、饱和度和性质有关。

Khalili等（1998年）对14种土进行试验后得出有效应力参数χ 和基质吸力之间的关系，并且绘制了有效应力参数χ 和基质吸力比（ua-uw）/（ua-uw）b之间的拟合曲线，得到有效应力参数χ 的近似表达式：

式中　（ua-uw）b ——土的进气值。

将式（1.2-7）带入式（1.2-6）可得

Khalili的这一试验成果表明尽管有效应力参数χ 因为受很多因素影响不易精确测定，但是通过式（1.2-8）可以从理论上近似估算非饱和土抗剪强度，说明Bishop的非饱和土的抗剪强度理论具有一定的实用价值。

Fredlund（1978）利用双变量（σ-ua）和（ua-uw）提出了非饱和土抗剪强度公式：

式中　φb——吸力内摩擦角。

该理论假设非饱和土抗剪强度与基质吸力呈线性比例关系，tanφb对同一土样为常数。Fredlund的非饱和土抗剪强度理论将破坏包络面扩展为三维平面，增加了变量基质吸力。在基质吸力恒定的前提下，莫尔圆与饱和土莫尔圆相同。在Fredlund提出非饱和土抗剪强度理论后，Fredlund等对这一理论做了进一步验证发现，非饱和土抗剪强度与基质吸力并不完全呈线性比例关系，即使对同一土样吸力内摩擦系数tanφb也不是常数，而是随基质吸力的变化而变化的。当土样接近饱和土时，吸力内摩擦系数tanφb接近饱和土的内摩擦系数tanφ；当饱和度降低时，吸力内摩擦系数tanφb随着吸力的减小而增大。

卢肇钧（1997年）将膨胀力作为非饱和土的吸附强度，并且提出吸附强度的计算公式：

式中　ms——膨胀力的有效系数；

　　　Ps——膨胀力。

1.2.1.4　非饱和土固结特性

饱和土固结理论以一维固结理论和比奥固结理论为核心形成了成熟的理论体系。在已经提出的非饱和土固结理论基本上以饱和土理论为基础，并引入了吸力，造成变量和方程非常多，数学模型复杂。国外从20世纪60年代开始研究非饱和土固结问题，典型的有Scott.R.F.，Barden.L，Licret A，Fredlund等人提出的固结方程，其中最为流行的为Fredlund固结理论。Fredlund和Hasan将非饱和土视为四相系，即在水、气、土粒之外增加了水气分界作为第四相。土粒和水汽的分界面在力的作用下处于平衡状态，在非饱和的条件下，空气和水同时发生流动。Fredlund和Hasan提出了两个偏微分方程来求解固结过程中孔隙水和孔隙气的变化。

液相偏微分方程：

气相偏微分方程：

Fredlund的固结理论可以看作Terzaghi固结理论的推广，概念明确，形式简单，最大的优点在于它放弃了有异议的非饱和土有效应力原理，代之以两个独立的应力状态变量外加应力（σ-ua）和（ua-uw）来建立非饱和土各相的体应变本构方程；但它也具有与Terzaghi固结理论类似的缺点，即假定总应力在固结过程中不变，本构方程中参数的测定也很困难。为了导出孔隙压力消散方程，采用了过多的与实际情况不大相符的简化假设。

Lloret和Alonso（1980年）以状态面代替本构方程，并结合连续方程及渗水、渗气的Darcy定律组成封闭方程，即：

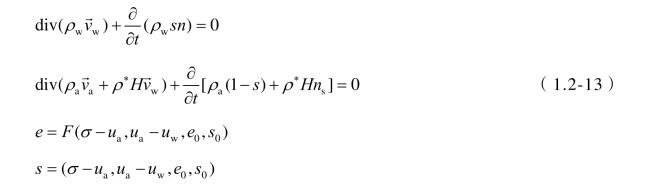
求解了非饱和土的固结和一维入渗时的膨胀问题和湿陷问题，从而拓宽了非饱和土固结的内涵。但模型没有参数化，不便于应用。

Rahardjo（1990）通过对非饱和粉砂进行K0固结试验，验证超静孔隙气压力几乎是在瞬间消散的，这个过程可以通过水的流动方程来描述非饱和土的固结过程，由此可将式（1.2-11）简化为：

Lloret和Benjamin（2000年）把混合物理论应用于三相介质，提出了确定非饱和土本构关系的三维模型，三相介质中每相都有其应力和应变，建立了弹性和弹-塑性本构方程。该本构方程要求最少的材料参数，直接包含了土-水特征曲线。对公式影响较大的是有效应力的确定，以及有效应力和吸力的耦合影响。该模型可以描述试验过程中观察到的许多土的固结特征。

国内在非饱和土固结理论问题的研究中，近年来取得了较大的进展。非饱和土的固结理论是20世纪90年代以来研究的热点，陈正汉（1989年，1991年）、杨代泉（1992年）和殷宗泽（1998年）曾先后研究过非饱和土的固结理论。目前，非饱和土的固结计算方法大体上归纳为3类：

（1）考虑孔隙混合流体消散的简化计算方法。魏云海等将土体假设为具有可压缩流体的两相土，考虑水气混合物的压缩性，推导出不排水条件下的压缩公式，建立非饱和土排水固结方程，并获得一维简化解析解。这种方法假设孔隙气以封闭气泡的形式存在于孔隙水中随水一起运动，忽略基质吸力，认为孔隙水压力等于孔隙气压力，因此只适用于高饱和度的非饱和土。

（2）主要考虑孔隙水压力消散的简化计算方法，适用于高饱和土体，如沈珠江方法。该方法假设孔隙气的排气率等于常量，建立非饱和土的简化固结理论，并应用于裂隙黏土中雨水渗入过程的数值模拟，得出了土体吸力丧失、有效应力降低和膨胀回弹的全过程，算例结果合理，只是有关孔隙气排气量的设定尚有待进一步研究。

（3）主要考虑孔隙气消散的简化计算方法，适用于饱和度不太高的情况，如杨代泉方法。杨代泉用水气连续方程、水气渗流的Darcy定律、土骨架的平衡方程、热量守恒方程、吸力状态方程等19个方程求得19个未知量：sij，eij和wi（土的位移）；ua，uw，T（温度）和s（饱和度）等。对一维固结条件，由于在孔隙气体未进入完全封闭状态之前，非饱和土的固结过程主要是排气过程，而且固结过程中饱和度的变化与瞬时加荷后饱和度的变化相比可以忽略不计，故此时非饱和土的固结问题就变成孔隙气压力的消散问题。他求得了简化的解析解，证明了它与数值解的一致性。他还提出了Fredlund关于非饱和土加载瞬时不排水、不排气分析方法中存在的问题，提出用水气连续方程、土在加载后的体变增量方程和吸力方程作为封闭方程，从而求出加载瞬时的Δua，Δuw，Δs，Δn，这个增量与加载前相应量之和即为固结的起始条件。

虽然对非饱和土进行了大量的研究，并取得了部分成果，但由于非饱和土的复杂性，还未形成便于操作和计算的非饱和土固结理论与沉降计算方法，通过原位试验、现场实测掌握非饱和土沉降特性，对于工程实践将具有急迫性和重要性。