室内模型试验：群桩中各单桩性状

(1)土与桩的特性参数

Gandhi&Selvam(1997)对一系列室内群桩模型试验的性状进行了分析,群桩布置如图7-6所示。试验在一个0.7 m×0.7 m×0.6 m试验槽中进行,槽中填土为细到中等颗粒大小的干河砂,砂土粒径组成如下：D10=0.22 mm,Cc=1.28,Cu=2.09,G=2.68,γmin=14.61 kN/m3和γmax=17.30 kN/m3。填砂相对密度Dr=60%,容重γs为16.22 kN/m3,内摩擦角φ取为36.3°(Schmertmann,1978)。土体泊松比假设为0.3。

模型桩由铝管制成,外径18.2 mm,壁厚0.75 mm,抗弯刚度为0.086 kN·m2。承台离砂面高度10 mm,每根桩的嵌入长度为500 mm,排内各桩中心距sp/d=3,改变排间距比ss/d考虑排距对群桩性状的影响。如果桩的位置沿荷载轴线对称,则假定它们的性状相同,因此,图7-6中编号相同的桩具有相同的性状。

(2)各桩的LFP分析

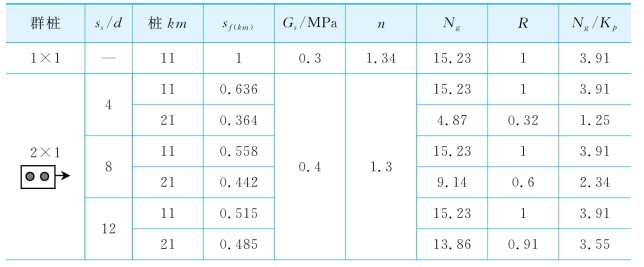
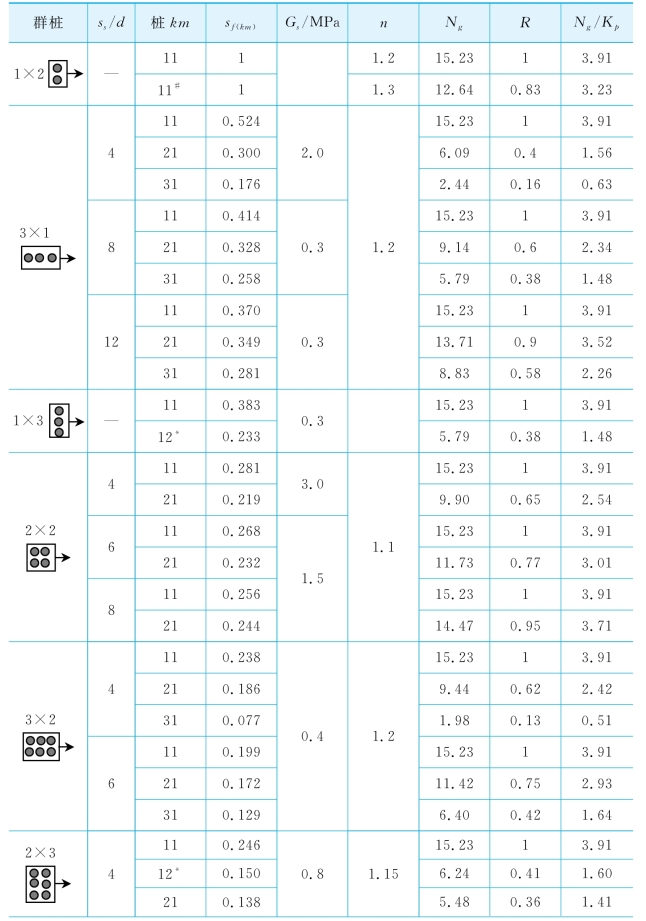
在本节的分析中,单桩km的荷载分配系数sf(km)见表7-7,由桩头位移为10 mm时分配在该桩上的荷载计算得到。值得注意的是,在模型试验中10 mm对应的荷载,除了单桩是直接测定的外,其他桩分配的荷载由桩头总荷载Pt结合如下假定(Gandhi&Selvam,1997)确定：

①2×1群桩(图7-6(b))中桩P11分配的荷载与桩头固定的单桩(图7-6(a))相同;

②3×1群桩(图7-6(d))前面两桩承担的桩头荷载与2×1群桩(图7-6(b))相同;

③1×3群桩(图7-6(g))中桩P11分担的桩头荷载与1×2群桩(图7-6(c))的P11相同;

④2×2群桩(图7-6(e))中桩P11分担与1×2群桩(图7-6(c))中P11相同的桩头荷载;

⑤3×2群桩(图7-6(f))中前两排桩分担与2×2群桩(图7-6(e))相同的荷载;

⑥2×3群桩(图7-6(h))的前排桩分担的荷载与1×3群桩(图7-6(g))相同;

⑦2×3(图7-6(h))或3×3群桩(图7-6(i))中,边桩与中间桩的荷载比对于各排相等;

⑧3×3群桩(图7-6(i))前两排分担的荷载与2×3群桩(图7-6(h))相同。

假定sf(km)为常数,因此可由程序GASLFP预测桩头荷载(Pt)-变形(yt)关系。各个桩的LFP(图7-6(a)～(i))可通过拟合实测和预测的Pt-yt曲线反分析确定。对于群桩中的桩P11,取α0=0和Ng=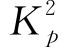=15.23(Barton,1982;Fleming等,1992;Guo,2003,2004),通过反分析得到n和Gs。然后,采用与桩P11相同的n值,通过拟合各自计算和实测的Pt-yt曲线反分析后排桩和前排中间桩(如果存在的话)的Ng和Gs值。一般地,对于同一群桩中的各个单桩,除非考虑桩的扰动效应(如加密效应),可取相同的Gs值。

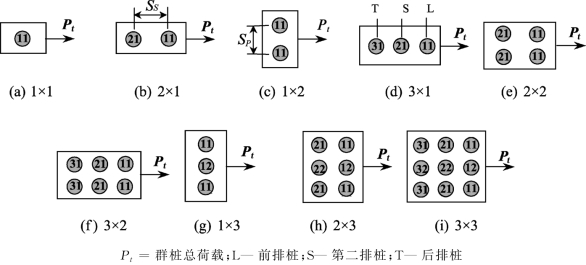
图7-6　群桩室内模型试验的布置(Gandhi&Selvam,1997)

(3)单桩

对于图7-6(a)中所示的打入单桩,通过拟合实测Pt-yt曲线,反分析得n和Gs分别为1.34 MPa和0.3 MPa。相应的实测和计算Pt-yt曲线如图7-7(a)所示,二者吻合很好。在最大荷载时,塑性滑移深度xp为12.7d。在xp深度内,反分析得到的LFP与Reese LFP和Broms LFP一同绘于图7-7(b)。反分析得到的LFP与Reese LFP十分接近,但远比Broms LFP大。

分别将Ng和Gs值或两者同时减少一半,预测的Pt-yt曲线也绘于图7-7。可以发现,桩的性状对Ng值比Gs值敏感,特别是在较高的荷载水平下。例如,在最大荷载时,桩头侧向位移从11.1 mm(Ng&Gs)分别增长到21.4 mm(0.5Ng)和13.8 mm(0.5Gs)以及24.5 mm(0.5Ng&0.5Gs)。根据该实例和其他实例的分析(Guo&Zhu,2004),如果最大塑性滑移深度小于2d时,桩的性状可能对Gs值比较敏感。否则,桩的性状主要受LFP控制(Guo,2002)。因此,在下面的实例分析中,主要讨论各单桩的位置对相应LFP的影响,特别是Ng的变化。

图7-7　单桩的性状和LFP

(4)2-桩群桩

对于不同桩间距ss/d(=4,8和12)的2×1群桩(图7-6(b))和1×2群桩(图7-6(c))的性状如图7-8所示。在图7-8中,对于桩P11的LFP和桩P21的LFP分别用点和线表示。同时还绘制了Reese LFP和Broms LFP。

对于ss/d=4的2×1群桩,预测的Pt-yt曲线如图7-8(b)所示,分别标记为P11-G和P21-G。预测的Pt-yt曲线与实测结果相当一致(图7-8(b))。对于桩P11和P21,最大荷载对应的滑移深度分别为13.7d和19.4d(没有在图中标出)。桩P11和P21最大荷载对应的最大弯矩分别为45.4 N·m2和32.5 N·m2。因此,对于给定的桩头荷载,前排桩的最大弯矩比后排桩的大(Brown等,1988)。(www.xing528.com)

如果采用Reese LFP预测ss/d=4的2×1群桩中P11和P21的桩头变形,在图7-8(b)分别计为P11-R和P21-R。预测的P11桩头变形与实测结果比较吻合,然而过低地预测了桩P21的变形。因此,直接将现有的LFP应用于群桩中的各桩,特别是后排桩的分析是不合适的。

从表7-8可以看出,对于不同ss/d的2×1群桩,桩P11的LFP参数均为：n=1.3,α0=0和Ng=15.23。并且,LFP几乎与单桩的LFP参数相同。对于后排桩,Ng=4.87(ss/d=4),9.14(8)和13.86(12),LFP似乎与ss/d有关。如果引入系数R,定义为各桩Ng值与桩P11的Ng值之比,则各桩的R值随着ss/d的增加而不断增长(图7-9)。

图7-8　2-桩群桩的LFP与性状

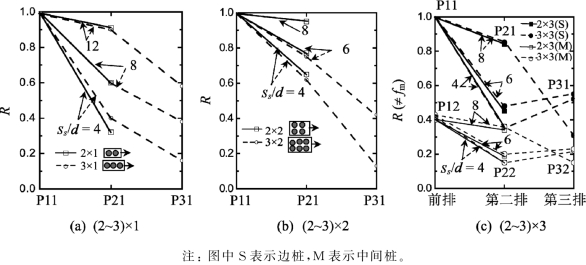
图7-9　各群桩中单桩的R值

对于1×2群桩,n=1.2,α0=0和Ng=15.23。n值比2×1群桩中桩P11的值稍小。由于只实测了桩顶位移,其他n和Ng(α0=0)值组合可能也能给出较好的2-桩群桩的性状预测。如对于1×2群桩,n=1.3,α0=0和Ng=12.64也能给出很好的桩基变形分析结果。

(5)其他群桩

从表7-8可以看出：①对于3×1(图7-6(d))),2×2(图7-6(e)),3×2(图7-6(f)),2×3(图7-6(h))和3×3(图7-6(i))群桩,n=1.08～1.2;②对于所有群桩中的桩P11,Ng=15.23和α0=0。因此,与单桩相比,除了n值稍低外,桩P11的LFP几乎与单桩的相同。

图7-9绘制了各群桩中单桩的R值。结果表明：①除了ss/d=8的3×3群桩的后排桩(P31和P32),第二和第三排桩的R值随ss/d值的增加而增大;②对于mg=3的群桩,前排和第二排桩的R值与相同ss/d的二桩排群桩相同。因此,Ng值与群桩的桩排数量无关;③对于ng=3的群桩(1×3,2×3或3×3),中间桩比边桩的R值小,因而中间桩比边桩发挥的土体抗力小。然而,二者的差距比群桩的离心机试验结果(Mc Vay等,1998)大,这将在下面进一步讨论。图7-10和图7-11只给出了ss/d=4的3×3群桩中各桩的荷载—变形关系。各桩分配的荷载随R值的增加而增长。

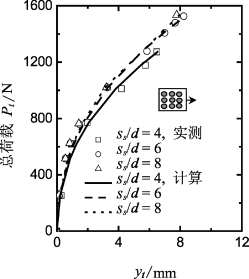
图7-10　3×3群桩的Pt-yt曲线

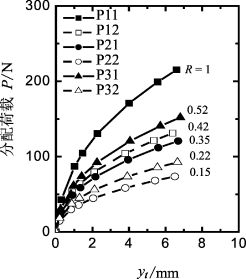
图7-11　ss/d=4的3×3群桩中各单桩P-yt曲线

表7-8　群桩模型试验分析中采用的土体参数

续表

续表

*：各排中的中间桩,其他为边桩。

(6)fm与系数R的关系

如果将群桩中每排桩作为一个分析整体,假设同一排内每个桩承担的荷载相等和性状相同,采用同一群桩中P11的Gs,n和α0值,通过拟合计算和实测的荷载-变形关系曲线,可以得到该排的等效Ng值。因为桩的性状一般由LFP控制而不是地基反力模量,则抗力折减系数fm近似等于各排的等效Ng值与同一群桩中桩P11的Ng值之比。

对于2×1～3×2群桩(图7-6(a)—(f)),fm与R值相等。对于2×3～3×3群桩,尽管各单桩的R值不同,前排桩的fm似乎与ss/d无关,大约为0.77～0.79。该值与ss/d=3的3×3群桩试验报道的0.8(Brown等,1988)非常一致。然而对于第二排桩,fm值为0.27(ss/d=4)～0.67(ss/d=8);3×3群桩的第三排,fm值为0.42(ss/d=4),0.43(ss/d=6)和0.25(ss/d=8)。因此,多桩排群桩中后排桩的fm可能为ss/d的函数。