土体侧向受荷桩性状及群桩分析方法

根据上述群桩分析的假定和模型,如果能够得到独立单桩在侧向荷载作用下的精确解答和群桩中各单桩分配的荷载大小,就比较容易得到群桩中各单桩的性状以及群桩的整体效应。

不考虑群桩施工引起土体性质的变化,则在群桩分析过程中,土体弹性参数(如剪切模量和泊松比)对各单桩分析都相同,并与独立单桩分析时相等。因此,由式(2-35)或式(2-45)可知,土体的地基反力模量也都相等。如果采用理想弹塑性p-y模型,由于桩—土—桩的相互作用,各单桩的极限抗力pu,即LFP,可能各不相同。

对于前排桩,如果已知独立单桩的LFP和分配在前排桩的荷载大小,那么,采用程序GASLFP或FDLLP就可直接计算前排桩的性状。单桩的LFP可通过单桩的现场载荷试验,按照第5章的分析过程,反分析得到。如果在缺少试验条件下,可根据第5章的LFP数据库选用。因此,关键的问题在于分配到前排桩的荷载大小。

对于后排桩,由上述群桩的简化分析阶段可知,由于前排桩的遮拦效应,相应的极限抗力比前排桩小。因此,对于后排桩的分析相对比较复杂,除了研究桩头分配的荷载大小,还必须考虑极限抗力的折减。

为了考虑桩头的荷载分配,引入分配系数Sf,定义如下：

式中,Pt=群桩总荷载;Pr=每排桩承担的总荷载。则作用在单个桩上的荷载P=Pt×Sf/ng。对于方形布置的群桩,目前,由试验报道的Sf值见表7-3。为叙述方便,对于第一排(即前排桩),将Sf计为Sf1,第二排计为Sf2,依此类推到第mg排。

表7-3　实测的荷载分配系数

(www.xing528.com)

续表

表7-4　由试验资料反分析得到的fm值

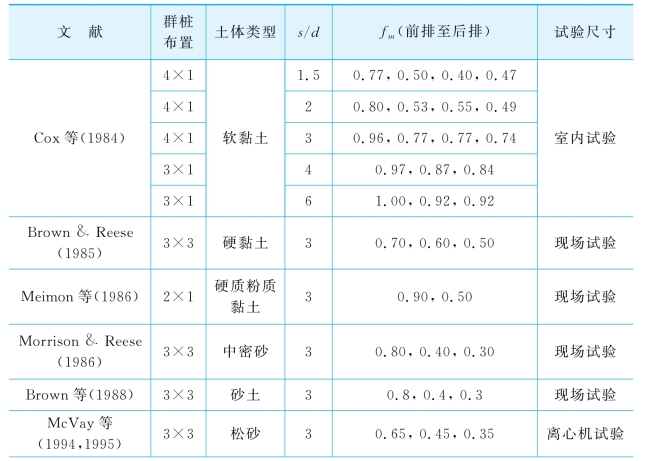
表7-3中的试验资料表明：①对于同一布置的群桩,随着桩中心距的增大,各排Sf的差距减小。当间距大于5d后(这与前面假定为6d比较接近),各排桩反应几乎相同;②前排桩的Sf最大,而中间排桩的Sf可能比后排桩的大,也可能比后排桩的小。为了考虑群桩效应引起土体抗力的降低,Brown等(1987)提出了抗力折减系数法,即在单桩p-y曲线基础上,对于相同的侧向变形y,将抗力p乘以折减系数fm,从而得到群桩中各单桩的p-y曲线)(Brown等,1988)。表7-4给出了一些研究者由群桩试验反分析得到的fm值。值得说明的是,采用不同的单桩p-y曲线,fm值可能不同,但主要取决于土体极限抗力的分布LFP。

续表

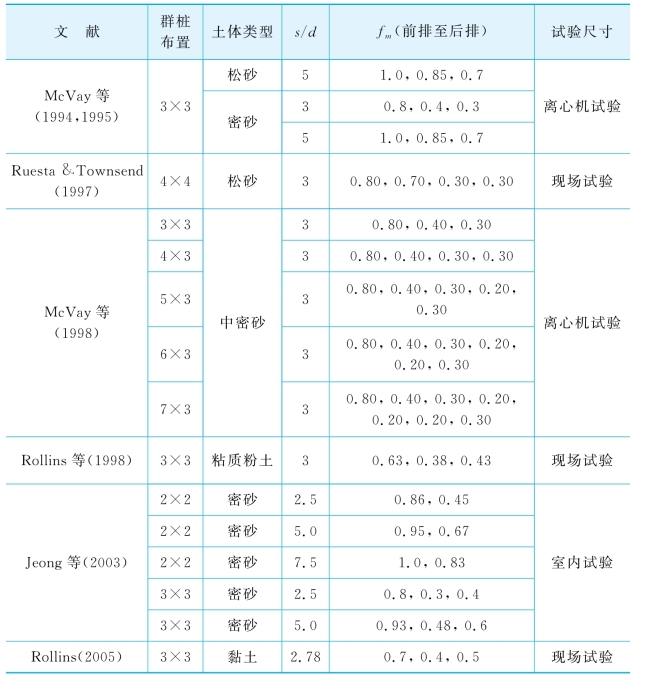
因此,如果已知独立单桩的LFP,参照表7-3选取每排桩的荷载分配系数Sf,采用程序GASLFP或FDLLP可以计算群桩中各单桩的性状,通过比较计算与实测的各桩荷载-变形关系,反分析得每排桩的fm值。同样,如果已知独立单桩的LFP,按照表7-4选取fm值(即地基反力模量和土体极限抗力同乘以表7-4中的系数),采用程序GASLFP或FDLLP可以计算群桩中各单桩的性状。通过比较计算与实测的各排桩荷载-变形关系,反分析得每排桩承担的荷载Sf。相反,如果已知独立单桩的LFP,按照表7-3和表7-4分别选取每排桩的荷载分配系数Sf和土体抗力折减系数fm,采用程序GASLFP或FDLLP就可直接预测群桩中每排桩的性状和群桩效应。由于本文采用理想p-y曲线模型和统一极限抗力分布,实际fm值可能与表7-4报道的结果不同。因此,本文将主要根据实测的桩基性状,讨论群桩中各桩的极限抗力分布。