土体极限抗力与侧向受荷桩性状案例分析

Reese(1997)报道了一个直径为1.22 m灌注桩的侧向载荷试验。该试验在Islamorada Florida Keys工程中进行(Reese& Nyman,1980),由Florida交通局资助。该场地岩层为易碎的,含晶簇珊瑚礁石灰岩。地面附近岩层的典型抗压强度为3.45 MPa。由于很难钻孔取样得到非扰动岩样,Reese(1997)认为RQD近似为零。根据岩石的分类,不连续结构间距可能小于60 mm(Bieniawski,1989)。由于在钻孔取样中可以发现很小的、由石膏粘接的不连续结构,可假定断层泥厚度小于5 mm。假定该场地岩体完全干燥,可得RMR89为34(Bieniawski,1989)和GSI为29。另外,根据试验轴向压缩试验得该岩体的平均杨氏模量Em为7.24 GPa,因此剪切模量Gm为2.9 GPa。

该试桩嵌入岩层深度为13.3 m,抗弯刚度EI=3.73 GN·m2。由桩的尺寸计算得截面惯性矩Ip为0.109 m4(不考虑钢筋的影响),则等效杨氏模量Ep为3.43×107kPa(=3.73×106/0.109)。取Ec≈Ep,混凝土的抗压强度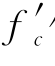估计为51.6 MPa。根据式(6-2),预测的开裂弯矩为798～1 276 kN·m(kr=19.7～31.5),其中,zt=d/2=0.61 m。

由于岩层上的砂土层由较大钢管护壁,荷载作用在地面附近,不考虑砂土层对桩性状的影响,则荷载作用在岩面上约3.51 m。

根据第5章实例RS7的线性分析结果,α0=0.2 m,n=2.5和AL=3.45 MN/m3.5(Ng=1.35),采用EI值和程序GASLFP预测的桩顶侧向变形如图6-38。根据计算或图6-38,当Pt大于300 kN后,实测的桩顶变形逐渐偏离计算桩顶变形。当Pt=300 kN时,计算的最大弯矩为1 161 kN·m,该值介于ACI方法预测的开裂弯矩范围内。因此,可取Mcr=1 161 kN·m,kr≈28.7。由于缺少钢筋数量和布置的相关资料,不能由MUEI直接计算(EI)cr值和由式(6-3)计算Pt大于300 kN后的EpIp值。因此,将上述岩体参数、LFP输入到程序GASLFP,通过拟合每一级荷载对应的计算桩顶变形和实测桩顶变形(图6-38(a)),反算出相应的EpIp值,如图6-40所示。与实例RN1相似,采用EpIp值得到的桩顶变形远比采用E I值得到的桩顶变形大,特别是在荷载水平较大的条件下。然而,二者给出的最大弯矩相差很小(6-38(b))。如在最大试验荷载Pt=667 kN条件下,桩顶变形从采用EI值的4.83 mm增加到采用EpIp值的18.0 mm(增长2.7倍);相应的,塑性滑移深度增长22.7%,从0.881 m(=0.72d)增加到1.084 m(=0.89d),然而,二者预测的最大弯矩同为2 674 kN·m。

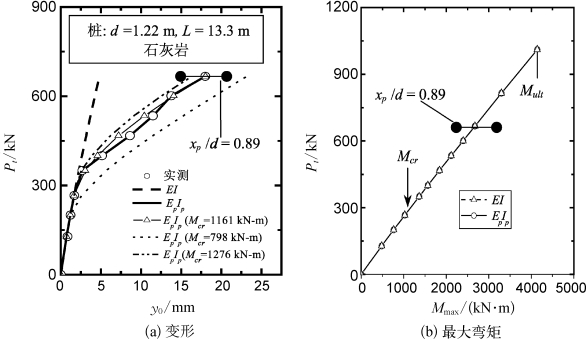
图6-38　Islamorada试验计算和实测桩基性状比较

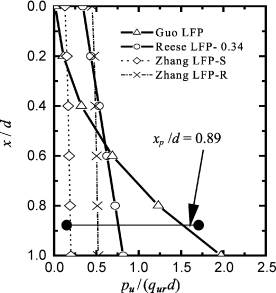
图6-39　Islamorada试验的LFP(www.xing528.com)

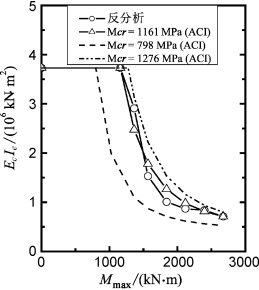
图6-40　Islamorada试验的EpIp

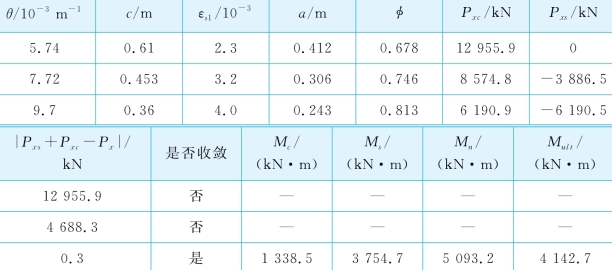
在最大试验荷载Pt=667 kN时,反算的E p I p值为0.71×106 kN·m2。将EpIp=0.71×106kN·m2,M max=2 674 kN-m和M cr=1 161 kN·m代入式(6-3),可求解得：Icr=0.012 9 m4和(E I)cr/E I=0.118。采用程序MUEI,不同的钢筋强度、钢筋数量和尺寸可得到几乎相同的Mcr和Icr。为了与实例RN1比较,采用与实例RN1相同的钢筋强度、钢筋尺寸和钢筋保护层厚度,即fy=496 MPa,ds=43 mm和t=0.18 m,将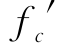=51.6 MPa和Ec=3.43×107kPa,输入到程序MUEI,当钢筋数量为20时,得到Icr=0.012 9 m4和Mult=4 142.7 kN·m。表6-18给出了3个代表性的迭代计算步结果,其中,Pxu=58.84 M N和Px=0。此时,钢筋的面积含量约为2.48%(=20×0.0432/1.222),比实例R1的1.46%(=40×0.0432/2.252)大,因此得到较大的kr和(EI)cr/EI值。

采用Mcr,Icr和EI值,可采用与实例RN1相同的步骤计算每一级荷载水平下的桩身最大弯矩、EpIp和桩顶变形。计算桩顶变形和EpIp值分别绘于图6-38(a)和图6-40。可以看出,计算EpIp与反分析得到的EpIp值,以及计算桩顶变形与实测值吻合相当好。值得指出的是,Mcr对EpIp值和相应的桩基性状有一定的影响。如图6-40,当取Mcr=798 kN·m和1 276 kN·m将分别得到与反分析结果小很多和稍大的EpIp值。相应的,在Pt=667 kN时,将分别得到28.5%高估和9.4%低估的桩顶变形。然而,在岩土工程中,计算误差在25%以内是可接受的。因此,在嵌岩桩分析中,采用ACI方法评价有效抗弯刚度是准确的。

表6-18　Islamorada试验实例中Mult的计算

在最大荷载对应的塑性滑移0.89d内,归一化极限抗力pu/(qurd)和Zhang LFP一同绘于图6-39。对于Zhang LFP,确定的参数为：mi=10,mb=0.792,s=0.000 37和m=0.5。与实例RN1相似,反分析得到的pu/(qurd)从岩面处的0.015逐渐增加到0.89d深度处的1.54。如果采用Reese LFPR,使0.89d深度内的pu/(qurd)平均值与反分析得到的值相等,则αr=0.34。而Zhang LFP-S和Zhang LFP-R得到的pu/(qurd)平均值远小于和接近于反分析结果。因此,采用αr=0.34的Reese LFPR和Zhang LFP-R也能得到合理的桩基性状。