土体极限抗力与侧向受荷桩性状

Zhang(2003)报道了在香港地区进行的两个大尺寸方形灌注桩(桩DB1和DB2)的现场侧向载荷试验。在该试验项目中,研究了方形桩在不同荷载作用方向下的性状。本节将对桩DB1分别在截面高度方向上和宽度方向上加载的性状进行分析,分别称为实例SN4和SN5。

桩DB1截面高2.8 m,宽0.86 m。桩长51.1 m,从上到下,横向加箍钢筋笼分别由24T32+24T25,28T25和24T20组成,保护层厚度为75～100 mm,钢筋屈服强度fy=460 MPa,取杨氏模量Es=2.0×108kPa;混凝土的杨氏模量Ec=3.03×107kPa,方形试样抗压强度fcu=53 MPa,则柱状试验的抗压强度fc′≈fcu/1.22=43.4 MPa(Beckett& Alexandrou,1997)。开裂前沿高度方向(称主方向)加载时,截面惯性矩Ip=1.573 2 m4,截面抗弯刚度E I=4.77×107kN·m2;沿宽度(次方向)加载时,截面惯性矩Ip=0.148 4 m4,截面抗弯刚度EI=4.50×106kN·m2。

采用ACI kr值,根据式(6-2)沿主方向加载时计算开裂弯矩为4.61～7.38 MN·m,其中,混凝土边缘距中性轴距离zt=h/2=1.4 m;沿次方向加载时计算开裂弯矩为1.42～2.27 MN·m,其中,混凝土边缘距中性轴距离zt=b/2=0.43 m。由实测结果表明,由于桩的侧向受荷性状主要发生在上部10 m内,仅计算上部截面的极限弯矩。采用MUEI计算得：沿主方向加载时,Mult=10.13 MN·m和(E I)cr=0.89 GN·m2;沿次方向加载时,Mult=2.98 MN·m和(EI)cr=71.26 MN·m2。

桩DB1试验场地属于围垦地,表层由粘质粉砂组成,夹杂鹅卵石。地面高程为+5.1 m,地下水位高程为+2.6 m。在地面下15 m(10d)范围内,平均标准贯入击数NSPT约为32.5,则可取Gs=0.4NSPT≈13.0 MPa;在地面下8 m(极限抗力可能发生最大深度5d)内,土体平均内摩擦角为49°。土体干容重为18 kN/m3,饱和容重为21 kN/m3(浮容重近似取11 kN/m3),地面下8 m深度内的有效容度γs=13.3 kN/m3。荷载近似作用在地面,即荷载偏心高度e=0。

(1)实例SN4的分析

由于夹杂鹅卵石引起表层土体内摩擦角过高,参照第5章的分析,保守估计Ng=0.55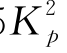=28.15,α0=0和n=1.7,相应的极限抗力分布与Reese LFP和Broms LFP同时绘于图6-18。采用EI值和程序GASLFP计算桩顶位移yt,如图6-19所示。在Pt小于约2.26 MN时,计算桩顶位移与实测值比较吻合;当大于该值时,实测值逐渐偏离计算值。取Pcr=2.26 MN,计算得最大弯矩为7.42 MN·m。该值比采用ACI kr值和式(6-2)计算的开裂弯矩大,因此可取Mcr=7.42 MN·m和kr≈31.7。

采用上述Mcr,(EI)cr,Gs和LFP,考虑抗弯刚度非线性特性,由GASLFP计算的桩顶位移和最大弯矩分别如图6-19和图6-20所示,相应的EpIp值绘于图6-21。计算结果表明：①在Pt≈3.61 MN时,桩的最大弯矩达到极限弯矩,同时,当Pt从3.0 MN增长到4.0 MN时,桩顶实测变形急剧增加,这表明桩在Pt=4.0 MN作用下可能发生了破坏;②采用ACI方法考虑桩的非线性,可以非常准确地预测桩顶变形;③在Pt=4.0 MN时,采用EpIp值计算得最大塑性滑移深度为2.8d,比采用EI值的计算结果(2.2d)大27.9%;④由于在主方向加载时,桩土相对刚度Ep/G*达1.1×105(对于一般的桩,Ep/G*=102～104),考虑桩的非线性后,桩身最大弯矩最大降低幅度达21%。因此对于长条形截面,混凝土开裂对最大弯矩存在一定的影响;⑤在1.5d深度内,土体极限抗力介于Reese LFP和Broms LFP之间;在(1.5～2.8d)范围内,土体极限抗力大于Reese LFP和Broms LFP得到的极限抗力;但在2.8d深度内,平均值接近Reese LFP。

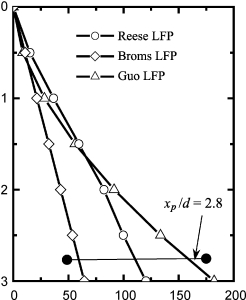
图6-18　桩DB1主方向加载的LFP

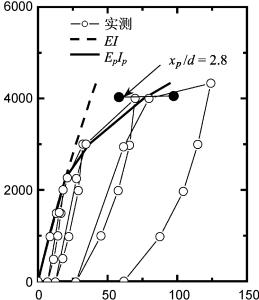
图6-19　桩DB1主方向加载实测与计算Pt-yt曲线

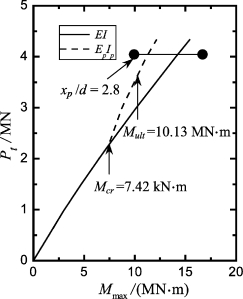
图6-20　桩DB1主方向加载实测与计算Pt-Mmax曲线

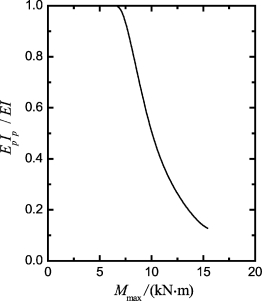
图6-21　桩DB1主方向加载EpIp-Mmax关系(www.xing528.com)

(2)实例SN5的分析

由于实例SN5没有实测资料,参照实例SN4,取kr≈31.7,则Mcr=2.28 MN·m,并采用下述两组参数进行分析：

组SN5_1：Gs=13.0 MPa,α0=0,n=1.7;Ng=0.55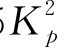=28.15;上述参数与实例SN4相同;

组SN5_2：Gs=13.0 MPa,α0=0和n=1.0;Ng=0.14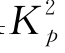=7.16;即采用极限抗力等于朗肯被动土压力(注意：由于加载方向上桩宽较大,可能表现出挡土墙的性质),如图6-22所示。

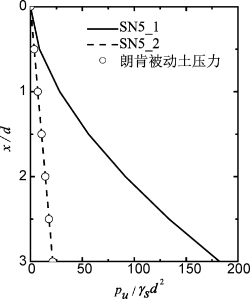
图6-22　桩DB1次方向加载的LFP

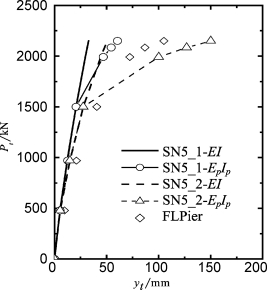
图6-23　桩DB1次方向加载的Pt-yt关系

采用上述Mcr,(EI)cr,Gs和LFP,考虑抗弯刚度非线性特性,由GASLFP计算桩顶位移和最大弯矩,分别如图6-23和图6-24所示,相应的EpIp值绘于图6-25。结果表明：①在Pt≈3.61 MN时,组SN5_1和组SN5_2计算的最大弯矩分别为2.78 MN·m和3.42 MN·m,二者均大于Mcr和MUEI计算的极限弯矩,因此,桩在该荷载水平下,受压侧混凝土发生压碎破坏,受拉侧则发生了开裂;②采用不同的极限抗力分布对侧向位移和桩身有效抗弯刚度影响显著,而对最大弯矩的影响较小。

比较采用Reese LFP和程序FLPier(Zhang,2003)得到的分析结果(图6-23)：①在开裂前,组SN5_2的分析结果与FLPier计算结果接近,这表明沿次方向加载时,桩DB1表现为挡土墙特性;②在开裂后,FLPier计算结果介于组SN5_1和组SN5_2分析结果之间,因此可以采用本文方法分析次方向加载时桩的非线性性状。

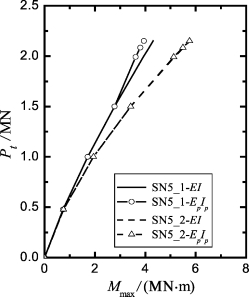
图6-24　桩DB1次方向加载的Pt-Mmax关系

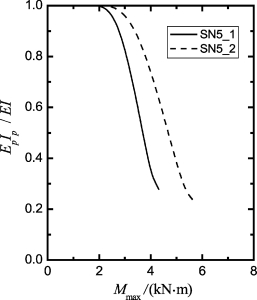
图6-25　桩DB1次方向加载的EpIp-Mmax关系