台湾试验实例SN1和SN2：土体极限抗力与桩性状

Huang等(2001)报道了在我国台湾地区进行的两个分别为钻孔灌注桩和预应力群桩和三个单桩(两个钻孔灌注桩B7,B13和一个预应力混凝土桩P7)现场侧向载荷试验。由于原文未报道桩B13的性状,这里只对单桩B7和P7进行非线性分析,分别称为实例SN1和SN2。

桩的结构组成如图6-5。桩B7长34.9 m,桩径1.5 m。横向加箍钢筋笼由52个直径为32 mm的钢筋组成,钢筋的强度fy=471 MPa,从钢筋布置图上量得保护层厚度约为50 mm;混凝土抗压强度f′c=27.5 MPa。开裂前桩截面抗弯刚度EI估计为6.86 GN·m2,桩截面惯性矩Ip=0.248 5 m4,则初始等效杨氏模量Ep=2.76×107kPa。采用ACI kr值,根据式(6-2)计算开裂弯矩为1.08～1.73 MN·m,其中混凝土边缘距中性轴距离zt=d/2=0.75 m。由MUEI计算得,Mult=8.77 MN·m和(EI)cr=1.02 GN·m2,相应的计算参数和结果见表6-8。

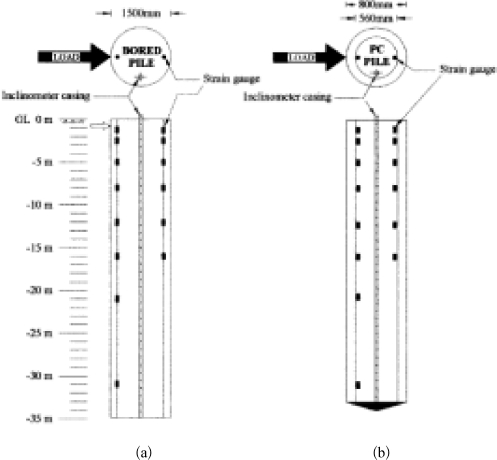
图6-5　桩B7和P7结构组成与钢筋布置图

桩P7为内部充填钢筋混凝土的预应力混凝土管桩,长34.0 m,桩径0.8 m。管桩外径0.8 m,内径0.56 m。预应力混凝土的抗压强度78.5 MPa,内填混凝土强度为20.6 MPa。横向加箍钢筋笼由19根直径为19 mm的钢筋和38根直径为9 mm的高强钢丝组成。预应力管桩内钢筋屈服强度fy=1 226 MPa,内部填充的钢筋强度为471 MPa,从钢筋布置图上近似可得管桩保护层厚度约为30 mm。开裂前桩截面抗弯刚度EI估计为0.79 GN·m2,初始等效杨氏模量Ep=3.93×107kPa。采用管桩混凝土强度和ACI kr值,由式(6-2)计算开裂弯矩为277.4～443.9 kN·m,其中混凝土边缘距中性轴距离zt=d/2=0.4 m。由于桩P7为混合材料,取桩的混凝土强度f′c近似为(Ep/151 000)2=67.74 MPa(而不是采用管桩或内填混凝土强度),由MUEI计算得,Mult=1.89 MN·m和(EI)cr/EI=0.146 MN·m2,相应的计算参数和结果见表6-8。

试验场地由相对均质的粉砂(SM)或粉土(ML)组成,偶见粉质黏土(CL)夹层。地下水位在地面下约1 m,由于未见土体重度的报道,假定土体平均有效重度为10 kN/m3。根据标贯试验,在地面下15 m深度范围内的平均贯入击数NSPT约16.9。根据表2-3,可插值得土体内摩擦角φ=32.6°。荷载近似作用在地面(e=0),如图6-5所示。

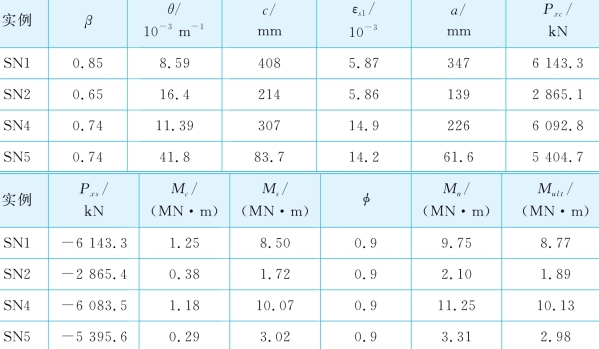
表6-8　砂土中桩的Mult计算

(1)实例SN1分析

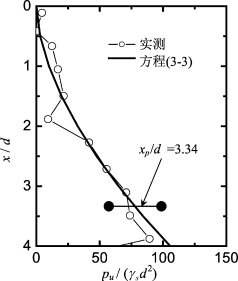
图6-6　桩B7的实测与拟合LFP

图6-7　桩B7的实测与计算Pt-yt曲线

根据现场DMT试验,桩B7的土体侧向极限抗力如图6-6。取n=1.7和α0=0,采用式(3-3)可拟合实测极限抗力得：Ng=0.9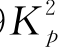=10.02。采用该LFP和EI值,取Gs=0.64 NSPT=10.8 MPa,应用程序GASLFP可得到如下结果：①Pt-yt曲线如图6-7所示。大约在Pt大于1 250 kN后,实测桩顶变形逐渐偏离计算桩顶变形;②在Pt=1 250 kN时,计算最大弯矩为3.45 MN·m,该值比采用ACI kr值和式(6-2)的计算结果大,表明桩在该荷载下开始发生开裂,即可取Mcr=3.45 MN·m(即kr=62.7)和Pcr=1 250 kN·m;(3)由计算极限弯矩Mult,反分析得Pult=2 571 kN;(4)在最大试验荷载Pt=2 943 kN时,计算最大弯矩为10.5 MN·m,该值大于计算Mult值。从实测桩顶变形可见,当桩顶荷载增大到Pt=2 943 kN时,桩顶位移变化仍比较平缓,表明桩在小于该荷载水平时,并没有发生极限破坏。因此,实测最大弯矩比计算极限弯矩大19.7%。在该实例中,得到比ACI方法大的开裂弯矩和比MUEI方法大的极限弯矩,可能部分归功于桩B7较高的配筋率以及桩周土体约束,其他原因不详。

采用Mcr=3.45 MN·m,根据6.3.2节的分析过程(或参照6.3.3节实例的分析过程),重新计算考虑抗弯刚度非线性特性的桩顶位移(图6-7)和最大弯矩(图6-8),其中部分荷载对应的桩顶变形、最大弯矩和塑性滑移深度如表6-9,相应的有效抗弯刚度绘于图6-9。计算结果表明：①开裂后采用EpIp计算得到的最大弯矩比开裂前采用EI值得到的最大弯矩差值在3.2%以内;②在Pt=2 571 kN(M ul t=8 773.5 kN·m)时,分析得到的桩顶位移比实测变形(97.1 mm)大1.15倍;③塑性滑移深度xp随开裂程度的增加而增长。在Pt=2 571 kN时,xp/d值从2.49增长到3.08,增长率为23.7%;④EpIp值比直接通过拟合桩顶实测位移反分析的结果小。在Pt=2 571 kN时,正分析EpIp/EI值为0.20,而反分析得到的值为0.61(比正分析结果大两倍)。因此,采用上述方法可能过高地估计了实例SN1的桩顶变形,但偏于安全。

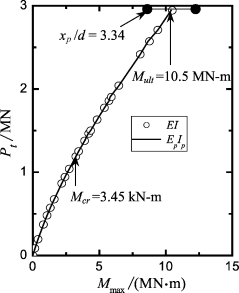
图6-8　桩B7的实测与计算Pt-Mmax曲线(www.xing528.com)

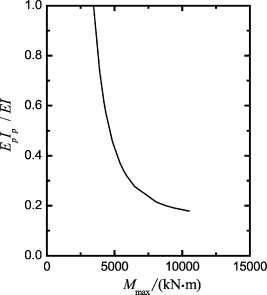
图6-9　桩B7的EpIp-Mmax关系

表6-9　桩B7非线性性状的预测

(2)实例SN2分析

根据现场DMT试验,桩P7的土体侧向极限抗力如图6-10所示。取n=1.7和α0=0,采用式(3-3)可拟合实测极限抗力得：Ng=1.0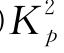=11.13。与桩B7相比,可以发现,由于桩的打入效应引起土体极限抗力增长约10%。采用该LFP和EI值,取Gs=0.64 NSPT=10.8 MPa,应用程序GASLFP可得到如下结果：①Pt-yt曲线如图6-11。大约在Pt大于284 kN后,实测桩顶变形逐渐偏离计算桩顶变形;②在Pt=284 kN时,计算最大弯矩为464.7 kN·m,该值比采用ACI kr值和式(6-2)的计算结果大,表明桩在该荷载下开始发生开裂,即可取Mcr=464.7 kN·m(即kr=33.0)和Pcr=284 kN·m;③由极限弯矩M ul t=1 886.0 kN·m反分析得：Pult=826.2 kN;④在P t=804和863 kN时,计算最大弯矩分别为18 180 kN·m和2 000.4 kN·m。从实测桩顶变形可见,当Pt从804 kN增大到863 kN时,桩顶位移显著增加。因此,桩在Pt在804～863 kN之间,确实发生了极限破坏。因此,计算极限弯矩是合理的。

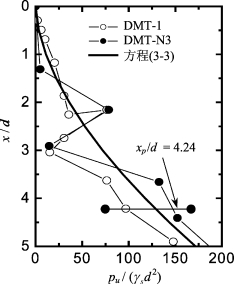
6-10 桩P7的实测与拟合LFP

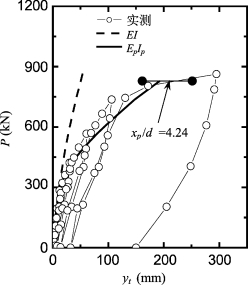
6-11 桩P7的实测与计算Pt-yt曲线

采用Mcr=464.7 kN·m,根据6.3.2节的分析过程(或参照6.3.3节实例的分析过程),计算考虑抗弯刚度非线性特性的桩顶位移和最大弯矩,分别如图6-11和图6-12所示,相应的EpIp结果如图6-13所示。其中部分荷载对应的桩顶变形、最大弯矩和塑性滑移深度见表6-10。比较采用EpIp值计算的桩顶位移和实测值发现,二者的最大误差在28%以内,因此,分析结果是合理的。其他结论与实例SN1相似。

表6-10　桩P7非线性性状的预测

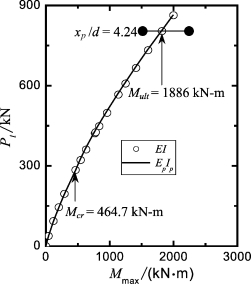
图6-12　桩P7的实测与计算Pt-Mmax曲线

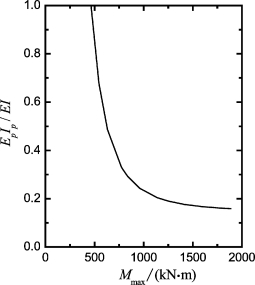
图6-13　桩P7的EpIp-Mmax关系