土体侧向受荷桩的Mult和(EI)cr差异

理论上,极限弯矩Mult和开裂后截面惯性矩Icr可通过弯曲理论进行计算。即根据混凝土和钢筋的应力应变关系,采用弯矩(M)-曲率(θ)法进行分析(如Hsu,1993)。然而,由于不同的混凝土和钢筋可能表现出不同的应力应变特性,很难给出Mult和Icr的显式表达式,往往借助复杂的数值分析过程,如Reese(1997)采用Hognestaad抛物线型混凝土应力应变关系和密布裂纹假定,给出了计算Mult和Icr的理论方法。然而,由于实际裂纹间存在一定的间距,并且混凝土的应力应变关系与多种因素(如混凝土强度,加载速率和持续时间等)有关,迄今还没有完全合理的弯曲理论计算Mult和Icr(Nilson等,2004)。因此,在设计中一般采用“简化矩形应力块”(Whitney,1937)极限状态设计方法。该方法被国外的混凝土结构设计规范广泛采用,如ACI 1993(美国);BSI 1985(英国);EC2 1992(欧洲);CSA(加拿大)和AS3600(澳大利亚)。

(1)简化矩形应力块计算模型

对于半径为r的圆形桩(图6-1(a))或截面高为h、宽为b的矩形截面桩(图6-1(b)),简化矩形应力块计算模型如图6-1所示(以桩截面内4排钢筋为例)。在极限状态时,桩可能发生两种破坏模式,即受压区混凝土发生破碎和受拉区钢筋拉伸破坏。对于第一种破坏模式,考虑到桩周土体的约束作用,破坏标准定义为混凝土极限抗压应变εcu=0.003 5(Nilson等,2004;BSI 1985;EC2 1992)(比ACI推荐的值0.003稍大)。对于第二种破坏模式,由于钢筋本身的破坏拉伸应变很大,在实际工程中很难发生,因此,规范中均未给出破坏标准(如ACI,1993;BSI,1985;EC2,1992)。但如果钢筋发生较大的应变,桩可能产生了过量的侧向变形。因此,为了限定桩的过量侧向变形,设定第二种破坏模式为：钢筋应变不超过极限拉伸应变εsu=0.015(Reese,1997)。

在简化矩形应力块法中,桩截面内应变线性变化(图6-1(c)),混凝土受压区内压应力均匀分布(图6-1(d))。受压强度σc=α1fc″=α1φcfc′,作用高度a=β1c,式中α1=平均应力系数,c=最边缘受压点到中性轴距离,φc=混凝土强度折减系数。对于第一种破坏模式,c=εcu/θ;对于第二种破坏模式,c=2r-t-ds/2-εsu/θ(圆形截面桩)或c=h-t-ds/2-εsu/θ(矩形截面桩),式中,θ为极限状态时的曲率,ds为钢筋直径和t为混凝土保护层厚度(图6-1(b))。

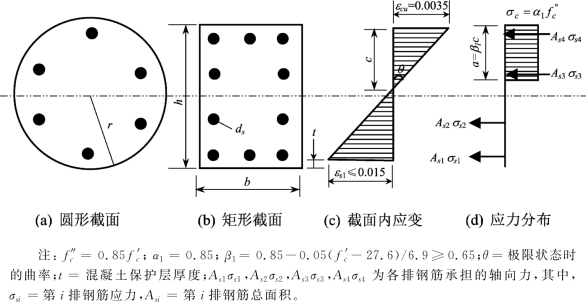
图6-1　简化矩形应力块模型

在图6-1中,钢筋按排编号,排号从受拉区到受压区,每排内的钢筋应力和应变相等。每排钢筋的应力计算如下：对于第i排钢筋,如果应变εsi超过屈服应变εsy=φrfy/Es,应力σsi=φrfy,式中Es=钢筋的杨氏模量;fy=钢筋的屈服强度,和φr=钢筋在拉伸和弯曲作用下的强度折减系数,取0.9;如果εsi小于屈服应变εsy,σsi=εsiEs。

根据截面内轴向力和弯矩的平衡,有如下方程：

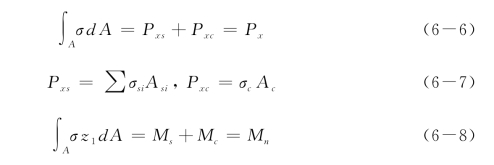
式中,A为截面内除受拉混凝土外的面积(包括钢筋面积和受压混凝土面积);σ为钢筋或混凝土轴向应力,即σsi或σc;Pxs和Pxc为分别为截面内钢筋和混凝土承担的轴向力;Px为截面内总轴向力;Ac为受压混凝土面积;Asi为第i排钢筋总面积;z1为研究点到中性轴距离;Ms和Mc为分别由钢筋和混凝土轴向力引起的关于中性轴的弯矩;Mn为名义或理论计算得到的极限弯矩。其中,Pxs,Pxc和Ms可以很容易得到,而Mc需要通过积分运算确定,特别是对于不规则桩截面。对于圆形截面桩和矩形截面桩(附录J),通过积分运算,Mc可表达为

圆形截面桩

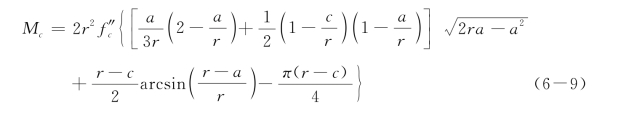
矩形截面桩

为了考虑桩的施工(如桩的尺寸不一致,钢筋笼偏位等)和“简化矩形应力块”模型中假定和简化引起的误差,设计极限弯矩可采用下式计算：

式中,ψ为极限弯矩折减系数。完全开裂后桩的抗弯刚度按下式计算：

(2)计算步骤

计算极限弯矩Mult和完全开裂后有效抗弯刚度(EI)cr的步骤可概括如下：

a.参数选取

εcu=0.035(=0.003～0.004),εsu=0.015,混凝土抗压强度fc′,钢筋屈服强度fy,混凝土平均应力系数α1;矩形应力块高度系数β1=0.85-0.05(fc′-27.6)/6.9≥0.65;钢筋强度折减系数φr(σr=φrfy);混凝土强度折减系数φc(σc=α1φcfc′)。对于上述各参数,不同的规范给出的值稍有差别(表6-1)。除了εcu外,本文推荐采用ACI建议的值。

表6-1　不同规范建议的设计参数

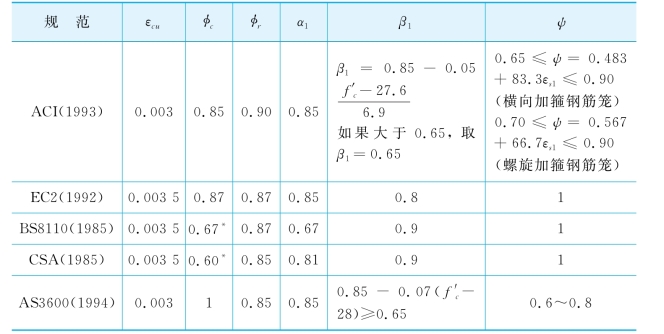
*：采用立方体混凝土试样抗压强度fcu,fcu与f′c值之间的关系可见Beckett&Alexandrou(1997),如对于C35,fcu约为1.286倍圆柱形混凝土块抗压强度fc′。(www.xing528.com)

b.迭代过程求解轴向力的平衡

①选定曲率θ(图6-1c)：对于圆形桩和矩形截面桩,第一次可分别假定θ=εcu/r和2εcu/h;然后,按指定的增量,如0.003 5/1 000r(圆形桩)或0.003 5/(1 000h/2)(矩形截面桩),增加(如果Pxs+Pxc-Px＞0)或降低(如果Pxs+Pxc-Px＜0);

②计算c=εcu/θ,α=β1c;

③采用式(6-7),分别计算钢筋和混凝土承担的轴向力Pxs和Pxc,并验算两者之和是否与该截面总轴向力相等和最大钢筋拉应变εs1是否小于0.015。轴向力收敛标准可取|Pxs+Pxc-Px|≤0.000 01Pxu,式中,Pxu=桩的轴向抗压强度=fc′Act+Es(fc′/Ec)As,Act和As=分别为混凝土和钢筋面积。如果缺少资料,Ec可采用桩的等效杨氏模量Ep代替;

④如果轴向力不平衡,重复步骤①—③,直到轴向力达到收敛标准,得到最终的c,a和θ值;如果εsmax＞0.015,重复步骤①—③,直到轴向力达到收敛标准,得到最终的c,a和θ,但需要注意的是,对于圆形桩和矩形截面桩,第一次选定的曲率θ应分别为θ=0.015/r和0.03/h;然后,按指定的增量,如0.015/1 000r(圆形桩)或0.015/(1 000h/2)(矩形截面桩),增加(如果Pxs+Pxc-Px＞0)或降低(如果Pxs+Pxc-Px＜0)。

c.计算截面弯矩

①采用式(6-9)(圆形截面桩)或式(6-10)(矩形截面桩)确定受压混凝土产生的弯矩;对于其他不规则截面桩,需采用积分运算过程计算混凝土压力产生的弯矩;

②计算受拉钢筋产生的截面弯矩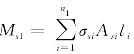,式中,n1=受拉钢筋排数,li=第i排钢筋离中性轴距离;

③计算受压钢筋产生的弯矩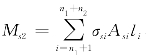,式中,n2=受压钢筋排数;

④根据式(6-8)计算名义极限弯矩Mn=Mc+Ms1+Ms2。

d.最后由式(6-11)和式(6-12)分别计算桩的设计极限弯矩Mult和完全开裂后有效抗弯刚度(EI)cr。

上述计算过程已编制成EXCEL2000电子表格计算程序MUEI。因此,下面Mult和(EI)cr的计算都基于程序MUEI。

(3)验证实例

实例1

直径d=450 mm的桩,混凝土保护层厚度t=30 mm,横向加箍钢筋笼由8根、沿桩周方向圆形均匀分布钢筋组成,混凝土抗压强度fc′=32 MPa,钢筋的杨氏模量Es=2×105MPa,混凝土杨氏模量Ec=2.71×104MPa,分别计算下述三种条件下的极限弯矩：①ds=28 mm,fy=500 MPa;②ds=28 mm,fy=400 MPa;③ds=24 mm,fy=400 MPa。

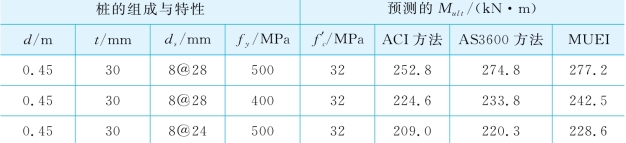
计算结果如表6-2。结果表明：①MUEI比ACI方法得到的设计极限弯矩大8%～10%(这是由于考虑桩周土体约束作用将εcu从0.003提高0.003 5的结果),比AS3600计算结果大1%～4%,因此,MUEI给出的设计极限弯矩是可靠的;②其他条件不变,当钢筋强度从500 MPa降低到400 MPa时,由MUEI得到的设计极限弯矩从277.2 kN·m降低242.5 kN·m,约为12.5%;③其他条件不变,当钢筋从28 mm降低到24 mm时,由MUEI得到的设计极限弯矩由277.2 kN·m降低至228.6 kN·m,约为17.5%。因此,钢筋强度和钢筋直径对极限弯矩都有较大的影响。

表6-2　实例1计算结果

实例2

直径d=2.25 m的桩,钢筋保护层厚度t=0.18 m,横向加箍钢筋笼由40根直径ds=43 mm、沿桩周方向圆形均匀分布钢筋组成,混凝土抗压强度fc′=34.5 MPa,钢筋屈服强度fy=496 MPa,钢筋的杨氏模量Es=2×105MPa,开裂前桩的抗弯刚度EI=35.15×106kN·m2。计算完全开裂后桩的等效抗弯刚度(EI)cr。

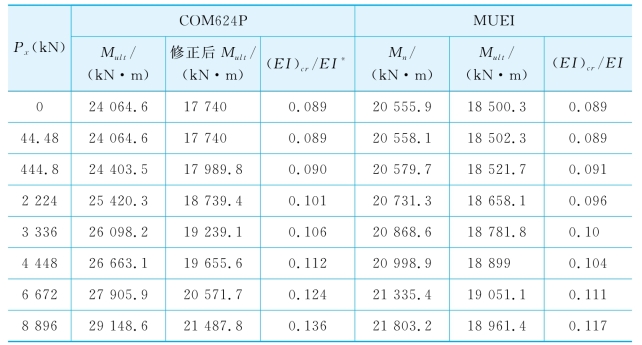
采用MUEI和COM624P(1993)分别计算完全开裂后桩的等效抗弯刚度,如表6-3。需要说明的是,COM624P(1993)可能由于内部计算错误,得到偏大的极限弯矩,因为Reese(1997)报道了一个与实例2相同的桩,当Px=0时,由LPILE Plus(COM624P的Windows版本)计算得Mult=17 740 kN·m。因此,当Px=0时,Mult值应修正为17 740 kN·m,对其他Mult值也同乘以系数0.737(=17 740/24 064.6),得到修正后的Mult值(表6-3)。修正后的Mult与MUEI预测的Mult,误差在12%以内。

由混凝土的抗压强度f′c=34.5 MPa,可得2.8×104MPa。采用MUEI计算(EI)cr值,相应的(EI)cr/EI值如表6-3。在轴向荷载Px小于444.8 kN时,采用MUEI得到的(EI)cr/EI值与修正后的COM624P计算值非常一致。然而,当Px大于444.8 kN后,随着荷载的增大,两者的差值越来越大,但误差在15%以内。总的来看,采用MUEI和COM624P预测的(EI)cr/EI值是比较一致的。值得指出的是,在Px=0条件下,完全开裂后的等效抗弯刚度(EI)cr仅为开裂前抗弯刚度EI值的9%(约降低10倍)。

表6-3　实例2计算结果

*：(EI)cr由修正后的极限弯矩计算。