Frantzen&Stratton(1987)报道了在美国Kansas城区四个不同场地进行的嵌岩桩侧向载荷试验。场地岩石分别为新鲜粘质页岩,风化粘质页岩,砂质页岩和砂岩。在每一场地,有两个4.57 m长、直径0.22 m、桩头自由的套管混凝土桩相互接近(分别称为南、北桩),互为反力桩,并承担相等的侧向荷载。由于在新鲜粘质页岩桩基施工中,桩与岩石之间存在空隙,本论文将不再讨论。在风化粘质页岩场地中,由于岩石的单轴抗压强度只有0.06 MPa,接近黏土的性质,从而可以按照黏土中侧向受荷桩的分析过程进行分析。因此,本文只对砂质页岩和砂岩中的情况进行分析,分别标记为实例RS1和RS2。相应的桩基参数如表5-11,岩石的分类指标和力学指标分别列入表5-12和表5-13。
由于试验中采用套管混凝土桩,套管的抗拉强度很大,内部混凝土提供的抗弯刚度较小,假定内部混凝土开裂后对桩的总抗弯刚度影响较小,故不考虑抗弯刚度的变化。根据报道的资料,E I=6.69 GN·m2,计算得Ep=5.815×107kPa。对于实例RS1和RS2,从报道的桩头变形测试位置,测量得荷载作用在岩面上的偏心高度e分别为0.61 m和0.82 m。因RS1和RS2的分析过程相似,下面只对实例RS1进行较详细的论述,RS2的分析结果可参见下一节侧向受荷嵌岩桩的分析数据库。
表5-11 嵌岩桩的计算参数
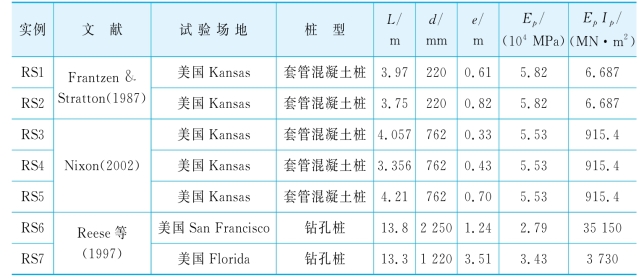
表5-12 岩石的强度和分类指标
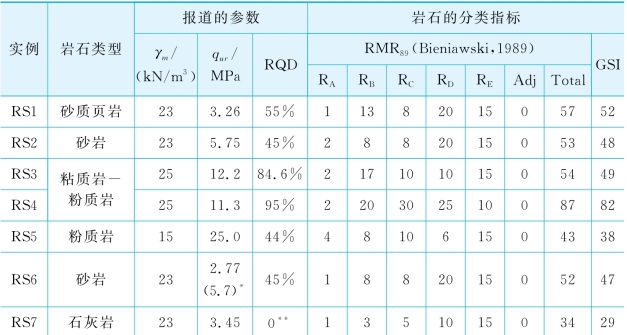
2.77(5.7)*:平均(典型)值;**:原始资料未报道,但Reese(1997)认为接近于零。
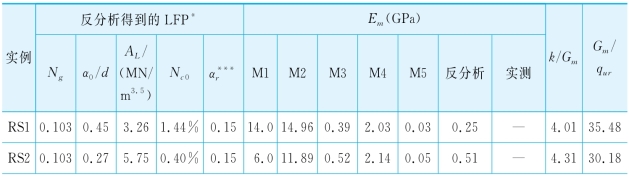
表5-13 岩石的其他力学指标
续表(https://www.xing528.com)
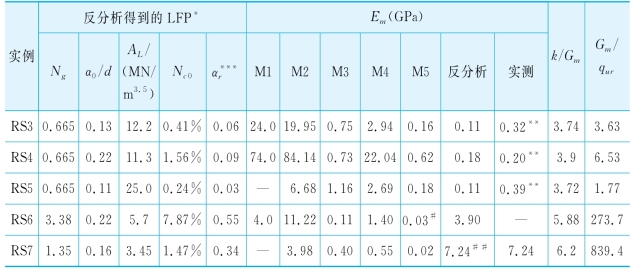
*:对于所有的实例n=2.5;**:岩面下三层岩石的平均值;***:如果采用Reese LFPR预测桩基性状时应采用的参数;
#:假设为开口裂隙;##:反分析值与Reese(1997)报道值相等。
在实例RS1中,砂质页岩的平均单轴抗压强度为3.26 MPa,平均RQD值为55%。因此,可假设岩体中不连续结构的间距为60~200 mm(Bieniawski,1989)。假定不连续结构的条件为“平均”状况,即“表面轻微粗糙,间距小于1 mm,岩壁高度风化”,并且砂质页岩完全干燥,则由Bieniawski(1989)的分类方法得RMR89=57,相应的GSI=52(表5-12)。
取n=2.5和AL=3.26 MN/m3.5,则由式(3-3)得Ng=0.103。采用程序GASLFP计算桩头变形,通过拟合预测与实测的桩基在岩面处的变形y0(如图5-20(a)),可反分析得如下参数:Gm=0.098 GPa(则Em=0.25 GPa)和α0=0.1 m(=0.45d)。将Gm和Ep代入式(2-19)得桩的有效长度Lcr=1.14 m(<桩的嵌入长度)。同时采用表5-8和5-9中的M1—M5方法确定Em经验值,如表5-13。可以看出,只有M3给出了比较合理的Em值。
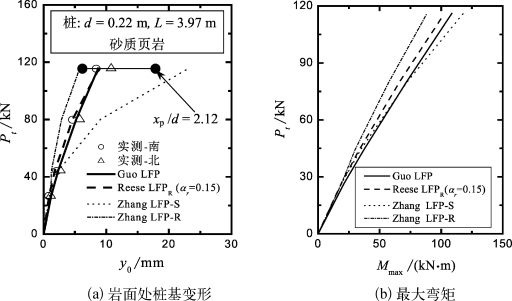
图5-20 Kansas砂质页岩中嵌岩桩的性状
在最大测试荷载Pt=115.6 kN时,计算得塑性滑移深度xp为0.466 m(=2.12d)。绘制该深度内无量纲极限抗力pu/(qurd)如图5-21(图中Guo LFP)。pu/(qurd)值从岩面处的0.014逐步增长到2.12d深度处的1.098。在xp深度内,pu/(qurd)的平均值与Reese LFPR采用αr=0.15时对应的值比较接近(图5-21)。同时αr=0.15的Reese LFPR可以采用式(3-3)进行拟合,拟合参数为n=1.35,Ng=0.12和α0=0.25 m。如果采用该Reese LFPR参数和程序GASLFP,预测的桩基变形也绘于图5-20(a),与实测结果也吻合很好。同时,分别采用Guo LFP和Reese LFPR得到的最大弯矩差别也不大(图5-20(b))。另外,图5-21也给出了Zhang LFP,其中,计算得到的参数为mi=12,mb=2.161,s=0.004 83和m=0.5。在2.12d深度内,由Zhang LFP-S和Zhang LFP-R得到的pu/(qurd)平均值分别小于和稍大于Guo LFP得到的pu/(qurd)平均值。相应的,Zhang LFP-S和Zhang LFP-R分别给出了过大和稍微过低的桩基变形预测,特别是在较大的荷载水平下(图5-20(a))。因此,只要最大塑性滑移深度内的LFP(包括形状和pu平均值)比较接近,不同的LFP(即不同的n,Ng和α0组合值)将给出比较一致的桩基性状预测;否则,将给出不同的结果。因此在实测资料有限的情况下,可假定n=2.5和AL=qur,由此引起的误差可由α0值进行补偿。
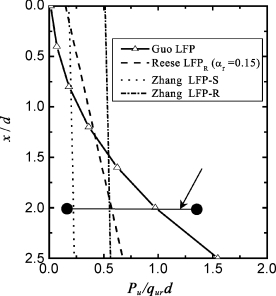
图5-21 Kansas砂质页岩中嵌岩桩的LFP
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




