黏性土中侧向受荷桩分析数据库：土体极限抗力与桩性状

对于黏性土,地面处土体极限抗力不为零,因此,α0＞0。根据第3章的分析,对于相对均质黏土,α0=0～0.4 m,n=0.7。但对于分层黏土,实例CS2的分析表明,n值可能不等于0.7。但对于不同的LFP,如果最大塑性滑移深度内平均值相近,分析结果比较一致,如果各层土体强度差别不大,仍可假定n=0.7,相应的误差可由Ng值得到补偿。除了上述实例CS1和CS2,表5-5和表5-6列出了其他30个分析实例的桩和土体参数。除了注明情况的实例外,采用GASLFP预测桩基性状与相应的实测结果非常吻合。相应的LFP和桩基性状可参见附录F,其中,J为Matlock LFP参数;c和φ为Hansen LFP参数,由拟合反分析得到的LFP确定。

表5-5　黏性土中侧向受荷桩数据库——桩参数

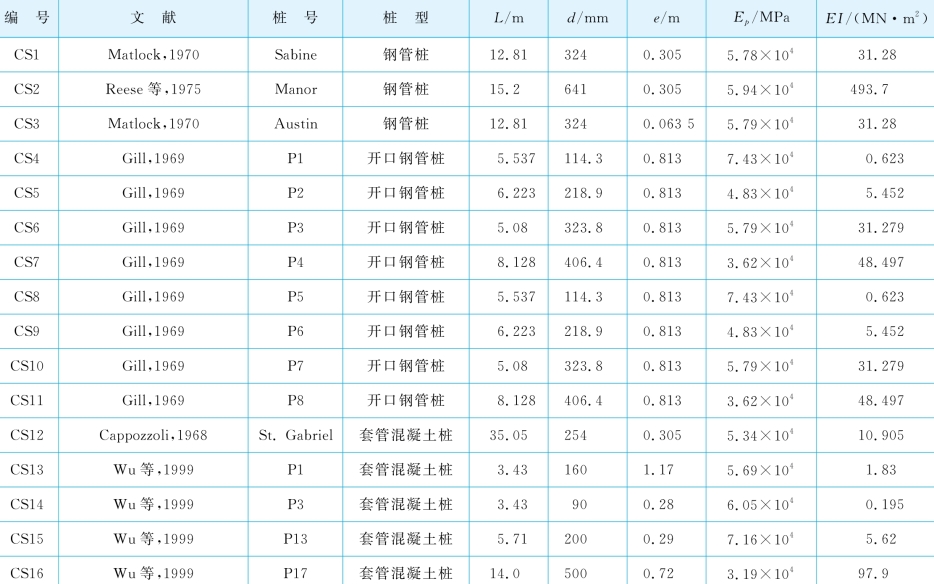
续表

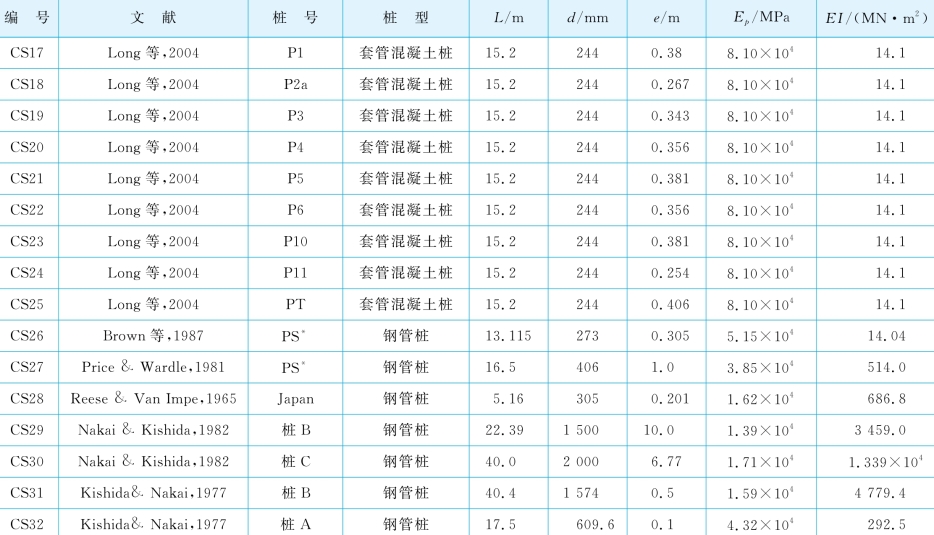
PS*：静载试桩。

表5-6　黏土中侧向受荷桩数据库——土体参数

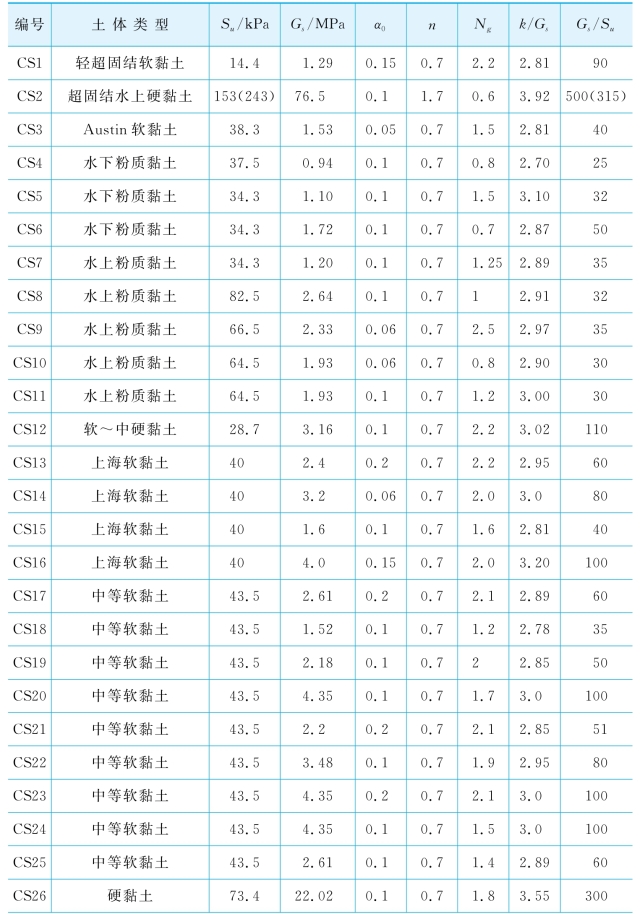
续表

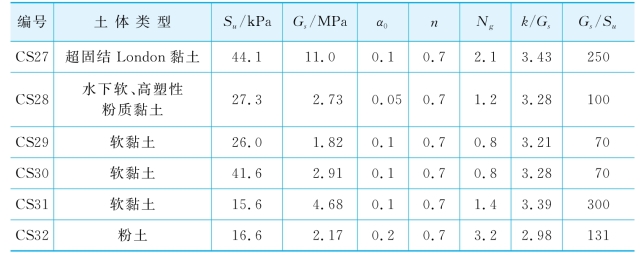
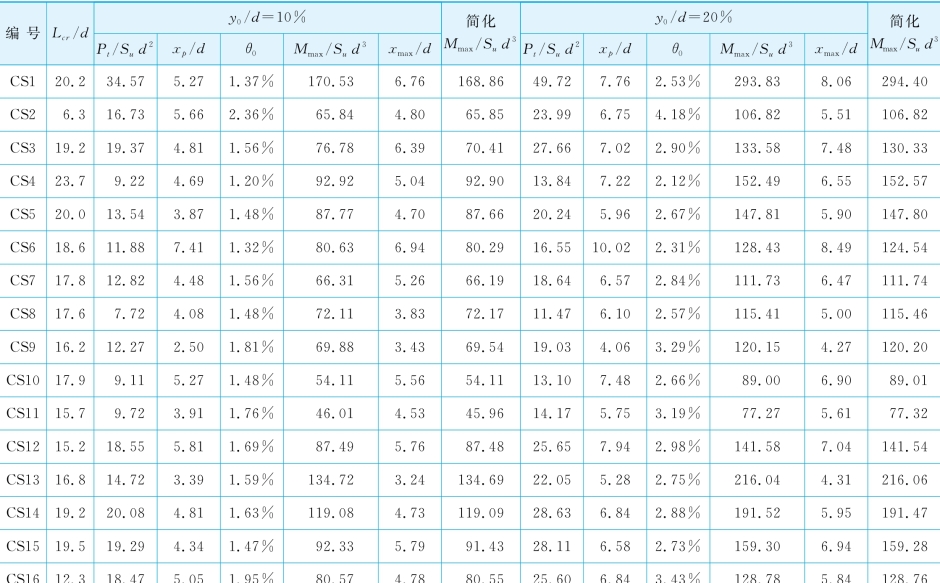
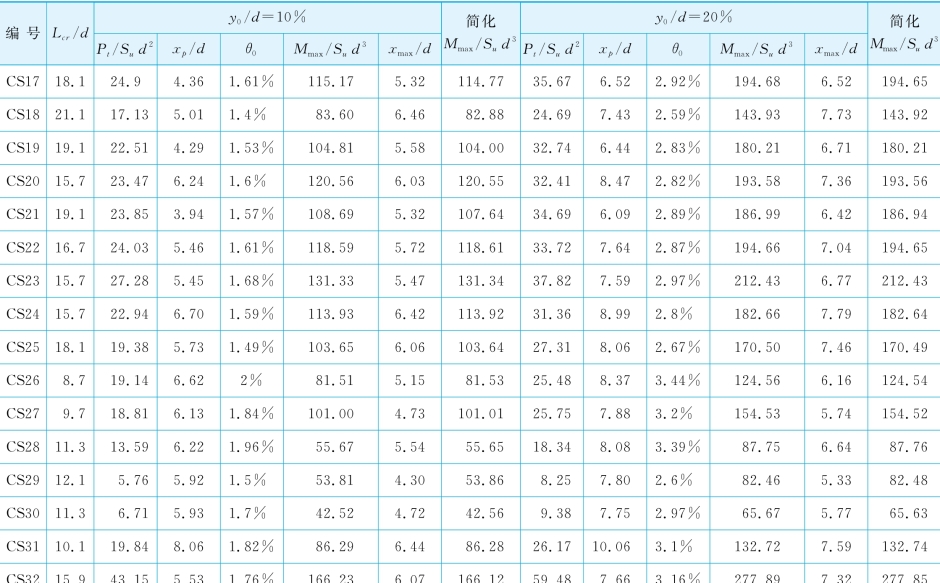
表5-7列出了地面处桩基变形分别为10%d和20%d的计算结果,包括：①归一化桩顶荷载Pt/Sud2;②归一化塑性滑移深度xp/d;③地面处桩的转角θ0;④归一化最大弯矩Mmax/Sud3;⑤归一化最大弯矩发生深度xmax/d。

根据表5-5—表5-7,可以得出如下结论：

(1)因为在上述数据库中,桩径d=0.09～2.0 m,不排水剪切强度Su=14.4～195.6 kPa,所以,分析结果既适用于微型桩,也可适用于大直径桩;既适用于软黏土,也适用于硬黏土;

(2)k=(2.7～3.92)Gs,平均值为3.04Gs。结果与砂土中的侧向受荷桩非常一致;

(3)Gs/Su=Ir=25～315,平均值为95Su,这与Duncan&Buchignani(1976)(图2-9)建议的Ir值变化范围比较吻合;(www.xing528.com)

(4)Ng=0.7～3.2,α0=0.05～0.2 m。考虑地面硬黏土的开裂或水力冲刷效应,α0可取零。上述结论适用于钻孔桩,也可适用于打入桩;

(5)当地面处侧向位移为10%d时,塑性滑移深度xp/d=2.5～8.06,平均值为5.19;最大弯矩发生深度xmax/d=3.24～7.41,平均值为5.35;当地面处侧向位移为20%d时,塑性滑移深度xp/d=4.06～10.06,平均值为7.26;最大弯矩发生深度xmax/d=4.27～10.02,平均值为6.56。因此,对于黏土中的侧向受荷桩,可选取(5～7)d深度内的平均不排水强度确定极限抗力;

(6)对于(5～7)d深度内相对均质土体,n=0.7;对于分层土体,n值可视土体组成条件而变化,一般而言,对于上软下硬土层,n值较大,对于上硬下软土层,n值较小;

表5-7　黏土中侧向受荷桩数据库——桩的计算性状

续表

(7)Lcr/d=6.3～23.1,平均值为16.1。对于柔性桩(即桩长大于Lcr),一般来说,桩基性状由上部10d深度内的土体控制,选择该深度内的土体平均参数确定地基反力模量k是准确的;

(8)由32个桩顶自由实例CS1—CS32,地面处桩基变形为10%d和20%d对应的地面转角分别为1.2%～2.37%(平均值分别为1.63%)和2.12%～4.22%(平均值2.91%)。因此,对于黏土中的侧向受荷桩,采用地面处转角约1.5%或3%为设计标准与采用地面处侧向变形为10%或20%基本上是一致的;

(9)将地面变形为10%d和20%d对应的Pt/Sud2和Mmax/Sud3与桩径的关系分别绘制在图5-12和图5-13。在地面变形为10%d时,Pt/Sud2=5.76～43.15,Mmax/Sud3=42.52～170.53;在地面变形为20%d时,Pt/Sud2=8.25～59.48,Mmax/Sud3=65.67～293.83。从图5-7和图5-8可以发现,Pt/Sud2和Mmax/Sud3值与桩径无关。

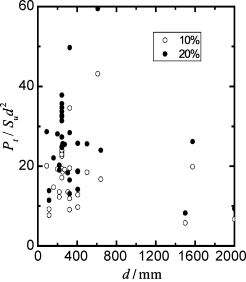
图5-12　Pt/Sud2～d关系

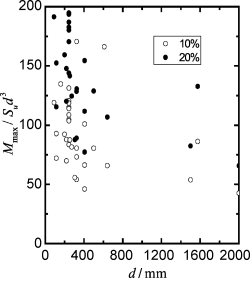
图5-13　Mmax/Sud3～d关系