土体极限抗力与侧向受荷桩性状分析

(1)实例CS1 相对均质土体

Matlock(1970)报道了一个黏土中钢管桩的侧向静力和循环载荷试验。该桩的桩径为324 mm,壁厚12.7 mm,长12.81 m,抗弯刚度E I=31.28 MN·m2,则Ep=EI/(πd4/64)=2.40×104MPa。根据桩截面的力学分析,出现塑性铰破坏时的极限弯矩为304 kN·m(Reese& Van Impe,2001)。本章主要论述桩的静载特性,因此只对静力载荷试验进行分析。

该试验位于美国得克萨斯州Sabine地区,是推导表2-13中CPY1模型的现场载荷试验,下称Sabine试验。土体为轻超固结海湘沉积黏土。土体相对均匀,不排水剪强度为14.4 kPa。在试验过程中,自由水面保持在地面高度。荷载作用在地面上0.305 m。

根据第3章的分析,取n=0.7。假定νs=0.3,采用程序GASLFP,首先通过准确拟合实测的最大弯矩Mmax(图5-10(c))、弯矩M沿深度分布(图5-10(d))和初步拟合实测荷载作用点处桩的变形(图5-10(b)),反分析得：α0=0.15 m和Ng=2.2。然后再通过调整Gs值,准确拟合实测荷载作用点处桩的变形(图5-10(b)),反分析得Gs≈1.29 MPa=90Su。从图5-10可见,预测的桩基性状与实测桩基性状相当吻合,并且比Reese&Van Impe(2001)预测结果更准确。

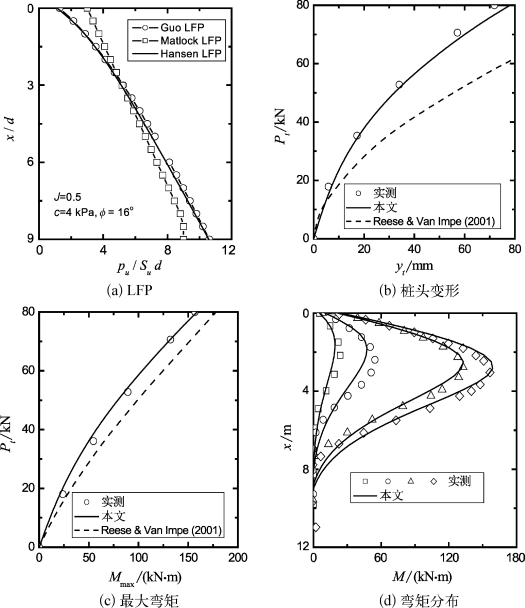
图5-10　Sabine试验LFP与桩基性状

在最大荷载Pt=80 kN时,M max=158.9 kN·m(＜Mu),塑性滑移深度xp为2.86 m(8.83d)。在该xp深度内,LFP与Matlock LFP(J=0.5)非常一致(图5-10(a)),并等效于c=4 kPa和φ=16°时的Hansen LFP。

将Gs和桩的等效杨氏模量Ep=5.79×104MPa代入式(2-19),可得桩的有效长度Lcr=6.54 m(=20.2d),该值小于桩长,因此该桩为柔性长桩。再将νs,Ep和Gs代入式(2-35)和式(2-45),可分别得到k/Gs=2.81和k/G*=2.43。

(2)实例CS2 分层土体(www.xing528.com)

Reese等(1975)报道了两个长15.2 m钢管桩的试验,分别为侧向静力和循环加载试验。桩的上部直径为0.641 m,下部0.610 m。由于侧向受荷桩的性状主要发生在上部,因此计算时采用直径d=0.641 m。桩截面惯性矩Ip=2.469×10-3m4,抗弯刚度E I=493.7 MN·m2,则Ep=EI/(πd4/64)=5.94×104MPa。桩的屈服弯矩My=1 757 kN·m,发生塑性铰破坏时的极限弯矩Mu=2 322 kN·m(Reese&Van Impe,2001)。本章主要论述桩的静载特性,因此只对静力载荷试验进行分析。

该试验位于美国得克萨斯州Manor附近。土体由地表附近的软黏土和深层强超固结黏土组成,如表5-4。土体不排水剪强度沿深度显著增长。由于试坑开挖深度约1 m,因此,取坑面下10d深度内Su=243.0 kPa用于确定地基反力模量;取坑面下5d深度内Su=153.0 kPa用于确定极限抗力分布。在试验过程中,自由水面保持在坑面高度,荷载作用在坑面上0.305 m。

表5-4　Manor现场试验土体组成(Reese&Van Impe,2001)

取νs=0.3,采用程序GASLFP,通过比较计算与实测的Pt-Mmax和Pty0关系曲线(图5-11),试算得：n=1.7,Gs=76.5 MPa=315Su,Ng=0.6和α0=0.1 m。从图5-11可见,预测的桩基性状和Reese等采用分层土体py曲线的预测结果一样,与实测桩基性状相当吻合。

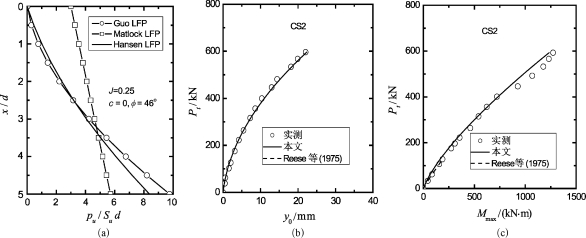
图5-11　Manor试验LFP与桩基性状

在最大荷载Pt=596 kN时,M max=1 242.3 kN·m(＜Mu),塑性滑移深度xp为2.72 m(4.24d)。在该xp深度内,LFP与Matlock LFP(J=0.5)显著不同(图5-11(a)),但接近于c=0 kPa和φ=46°(特密砂)时的Hansen LFP。同时比较n,Ng和α0与砂土中的相应值,可以发现,除了α0≠0外,LFP与砂土的LFP十分相似。因此,对于不排水强度沿深度显著增长的土体,LFP接近于砂土的LFP。综合实例CS1和CS2,结果表明,对于相对均质土体,n=0.7;对于分层明显的土体,应合理选择n值。一般的,对于上硬下软的分层土体,n可能小于0.7;对于上软下硬的分层土体,n的取值范围在0.7～1.7之间。

将Gs和Ep值代入式(2-19)可得桩的有效长度Lcr=4.05 m(=6.3d),该值小于桩长,因此该桩为柔性长桩。再将νs,Ep和Gs代入式(2-35)和式(2-45),可分别得到k/Gs=3.92和k/G*=4.3。后者得到的k值是前者结果的1.36倍。如第2章所述,由于轴对称有限元分析没有考虑桩后土体的拉裂而得到较高的土体刚度,由式(2-45)计算地基反力模量除以系数1.3是合适的,从而避免采用Bessel函数。