砂土中侧向受荷桩性状分析数据库

除了实例SS1外,本文还对其他19个砂土中的侧向受荷桩性状进行了分析。桩和土体的计算参数分别如表5-1和表5-2。在这些分析实例中(下称数据库),试验荷载水平可能并不一样。有的试验已经达到桩基破坏,有的则没有达到破坏。但在工程设计中,往往将一定的桩基变形或转角对应的荷载作为设计荷载(Kulhawy& Manye,1995)。因此,表5-3给出了地面处桩基变形分别为10%d和20%d的如下计算结果：①归一化桩顶荷载Pt/γsd3;②归一化塑性滑移深度xp/d;③地面处桩的转角θ0;④归一化最大弯矩Mmax/γsd3;和⑤归一化最大弯矩发生深度xmax/d。除注明情况的实例之外,计算桩基性状与相应的实测结果非常吻合,二者的比较可参见附录C。

在该数据库中,存在如下特性：①桩径d=0.018 2～0.812 8 m,内摩擦角φ=29.6°～43°;②包括现场试验、离心机试验和室内模量试验;③桩基有开口和闭口钢管桩、增强钢管桩、增强H型桩、套管混凝土桩以及铝管模型桩,可不考虑桩身屈服或开裂引起桩身抗弯刚度的衰减;④由于侧向受荷桩试验很难控制桩头为完全固定,因此只报道了两个桩头固定的室内模型试验结果,其他均为桩头自由桩。

根据表5-1、表5-2和表5-3,可以得出如下结论：

(1)由于在上述数据库中,桩径d=0.018 2～0.812 8 m,内摩擦角φ=29.6°～43°。因此,分析结果既适用于微型桩,也可适用于大直径桩;既适用于松砂,也适用于密砂;

(2)k=(2.38～3.73)Gs=(0.92～1.43)Es,平均值为3.23Gs或1.24Es。上述结果不仅与表2-6所列的α1值比较一致,而且与英国设计规范(CIRIA,1984)推荐的k=(0.8～1.8)Es非常吻合;

表5-1　砂土中侧向受荷桩数据库——桩参数

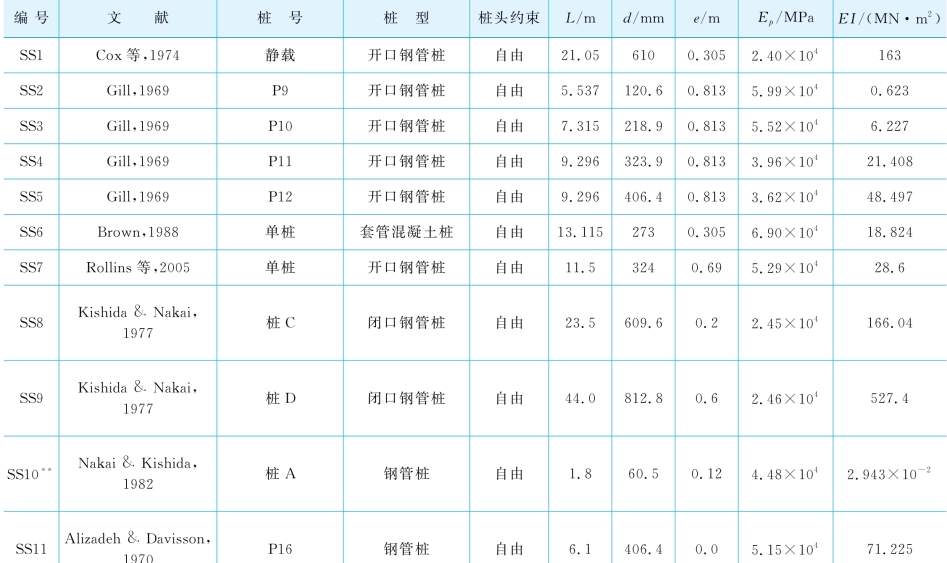
续表

桩号：原文报道的试桩编号或试验场地名;SS10* ：拟合地面位移和最大弯矩发生深度,实测最大弯矩偏小,很难拟合。
SS12& ：分析中采用Reese&VanImpe(2001)报道的土体参数以及角钢增强后桩宽(480.3mm);** ：原文未报道e 值大小,本文假定荷载施加在承台上部;*** ：采用程序FDLLP进行分析。

表5-2　砂土中侧向受荷桩数据库——土体参数

*：由于NSPT较大,内摩擦角采用Reese&VanImpe(2001)报道的平均值43°而非Alizadeh &Davisson(1970)给出的31°～35°。

表5-3　砂土中侧向受荷桩数据库——桩的计算性状

(www.xing528.com)

(3)Gs=(0.25～0.62)NSPT(MPa),平均值为0.50NSPT(MPa)。相应的土体杨氏模量Es=(0.65～1.6)NSPT(MPa),平均值为1.3NSPT(MPa)。该结果与大量报道的土体剪切模量或杨氏模量值非常一致,如Kulhawy& Mayne(1990)总结的Es值为(0.5～1.5)NSPT(MPa),Kishida& Nakai(1977)建议日本砂土Es=(1.4～1.8)NSPT。因此,采用侧向受荷桩试验可以准确反分析土体杨氏(或变形)模量,用于其他地下结构或基础的变形分析;

(4)Ng=(0.55～2.5)p,α0=0 m和n=1.7。对于挤土桩(如闭口钢管桩)和截面加强桩(如SS11—SS14),Ng=(1.0～2.5);对于部分挤土桩和钻孔桩,Ng=(0.4～1.6);

(5)Lcr/d=7.4～16.1,平均值为10.3。因此,一般选择10d深度内的土体平均弹性参数确定地基反力模量k是准确的;

(6)根据18个桩顶自由桩实例(SS1—SS18),当地面处桩基变形为10%d时,塑性滑移深度xp/d=1.63～5.18,平均值为3.60;最大弯矩发生深度xmax/d=3.35～6.10,平均值为4.07;当地面处桩基变形为20%d时,塑性滑移深度xp/d=2.22～6.39,平均值为4.61;最大弯矩发生深度xmax/d=3.85～6.55,平均值为4.67。因此,对于砂土中的侧向受荷桩,可选取5d深度内的土体重度、内摩擦角确定土体的极限抗力;

(7)根据18个桩顶自由桩的实例(SS1—SS18),地面处桩的变形为10%d和20%d时,对应的地面处桩的转角分别为1.45%～2.95%和2.85%～5.41%,平均值分别为2.17%和4.03%。因此,采用地面处转角为2%或4%为设计标准与采用地面处桩基变形为10%和20%基本上是一致的;

(8)比较SS12—SS15(加宽桩径)与SS11(未加宽桩径)的Ng值可知,增大桩宽可提高土体的极限抗力;

(9)比较SS18—SS20的Ng值可见,砂土中打入桩比钻孔桩的土体极限抗力大,桩头自由桩的土体极限抗力比桩头固定桩的土体极限抗力大。因此,土体极限抗力不仅与施工条件有关,还与桩头约束条件有关。比较反分析得到的LFP与Reese LFP,Barton LFP和Broms LFP表明(参见附录C),实际的LFP接近或大于上述三个LFP。因此,目前常采用的LFP(Reese LFP,Barton LFP和Broms LFP)可能只适用于钻孔桩或少量排土桩;

(10)分别采用式(2-35)和式(2-45)得到的k/Gs和k/G*值非常一致。如第2章所述,由于轴对称有限元分析没有考虑桩后土体的拉裂而得到较高的土体刚度,可将式(2-45)中的G*替换为Gs,或将式(2-45)除以系数1.3(略大于1+0.75νs),用于计算k值,从而避免采用Bessel函数;

(11)将地面处变形为10%d和20%d对应的Pt/γsd3和Mmax/γsd4与桩径关系分别绘制于图5-2和图5-3。可以看出,在地面变形为10%d时,Pt/γsd3=80～800,Mmax/γsd4=250～4 000;在地面变形为20%d时,Pt/γsd3=130～1 300,Mmax/γsd4=460～6 550。并且,Pt/γsd3和Mmax/γsd4值随桩径的增长呈降低趋势。

图5-2　Pt/γsd3～d关系

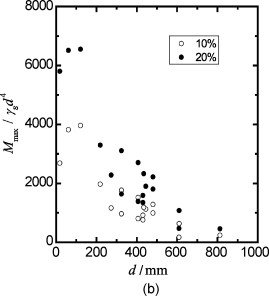
图5-3　Mmax/γsd4～d关系

值得指出的是,只要最大塑性滑移深度内的极限抗力平均值接近,形状相近的不同LFP可以得到比较一致的桩基性状。因此,对于砂土中侧向受荷桩的设计,可选取α0=0 m和n=1.7。对于分层土体,n=1.7与实际n值的差别可通过选取合适的Ng值得到补偿。