桩头约束对桩基性状的影响及极限寿命

采用程序FDLLP,可对桩头约束条件的影响进行研究。对上述假想的实例,采用与上述FDLLP分析相同的计算参数,图4-7给出了桩头自由、固定和部分固定(假设Mt/θt=1 000 kN·m/1)三种不同的桩头约束条件下的桩基性状。可以看出：

(1)桩头约束对桩的侧向变形y0影响十分显著(图4-7(a))。桩头自由时桩的侧向变形最大,桩头固定时变形最小。当Pt=300 kN时,桩头自由时的y0值是桩头固定时y0值的5.67倍,该值比一般的弹性解结果大(采用弹性解时二者的比值一般为2倍左右,如Kubo,1965)。

(2)桩头约束对桩的最大弯矩Mmax影响比较明显(图4-7(b))。桩头自由时,Mmax最大,部分固定时,Mmax最小。因此,采用部分约束的桩基不仅能降低桩的变形,而且能显著降低桩的最大弯矩。当Pt=300 kN时,桩头自由时的Mmax值是桩头部分固定时Mmax值的1.66倍。

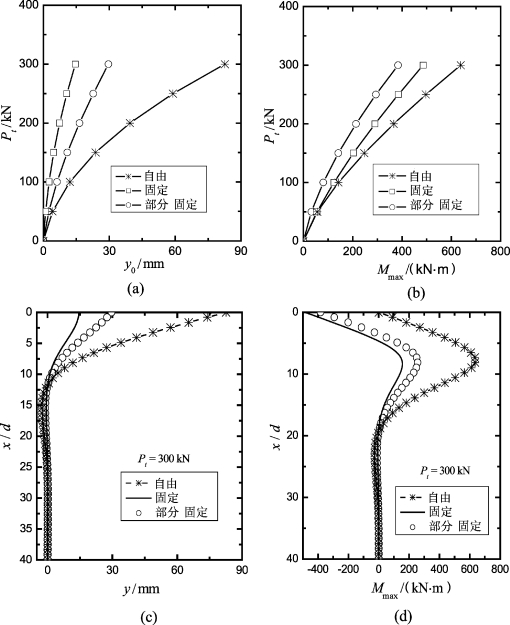
图4-7　桩头约束对桩基性状的影响

(3)无论哪种约束,桩的侧向变形主要发生在上部10d深度内(图4-7(c)),而弯矩主要发生在上部15d深度内(图4-7(d))。由于弯矩主要受上部土体极限抗力分布影响,所以选取10d深度内土体的平均弹性参数(Gs和νs),对任何桩顶约束条件都是合适的。

(4)在任意荷载水平下,桩头固定和部分固定时,最大正弯矩+Mmax和最大负弯矩-Mmax绝对值之和与桩头自由时的最大正弯矩Mmax有一定的差别,但差别不是太大。例如,当Pt=300 kN时,桩头固定和部分固定时,+Mmax与-Mmax绝对值之和分别为643.7 kN·m和640.1 kN·m,而桩头自由时的最大正弯矩Mmax为637.9 kN·m;当P t=100 kN时,桩头固定和部分固定对应的+Mmaxx与-Mmax绝对值之和分别为155.1 kN-m和147.5 kN·m,而桩头自由时的最大正弯矩Mmax为142.0 kN·m。因此,在工程实践中,可近似认为它们是相等的。(www.xing528.com)

另外,如果桩头为部分固定时,桩的性状与Mt/θt的大小有关。对上述实例,图4-8给出了Pt=300 kN时桩头变形和最大弯矩随Mt/θt值的变化关系。结果表明：

(1)随着Mt/θt的增长,桩顶变形在初始阶段急剧降低,然后趋于平缓(图4-8(a));

(2)随着Mt/θt的增长,在初始阶段,最大负弯矩急剧增长而最大正弯矩急剧降低;随后二者变化逐渐趋缓(图4-8(b));

(3)桩头自由和桩头固定条件并不是Mt/θt值分别为无限小和无限大的情况。当Mt/θt≈1 kN·m/1时,部分固定条件得到的桩头变形和最大正弯矩与桩头自由条件时对应的值相等;当Mt/θt分别为2 150 kN·m/1和2 780 kN·m/1时,部分固定条件得到的桩头变形和最大负弯矩分别达到桩头固定时对应的值,两者并不能同时吻合。因此,如果桩的设计由最大弯矩控制,在设计荷载条件下,最大正弯矩与最大负弯矩相等(即图4-8(b)中+Mmax与-Mmax的交点)对应的Mt/θt值即为最优桩顶约束。

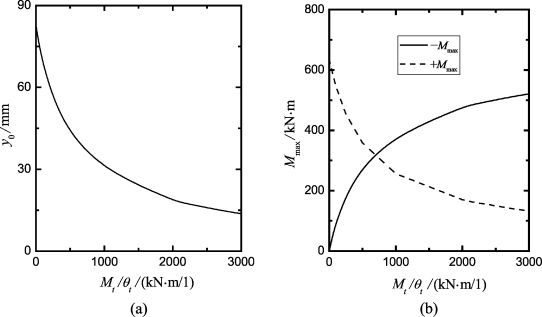
图4-8　桩头约束对桩头变形和最大弯矩的影响