差分求解土体极限抗力与桩性状

(1)微分方程的差分格式

采用Taylor级数展开桩的侧向变形函数y,可以得到x=xm+1和xm-1深度处的变形ym+1和ym-1如下：

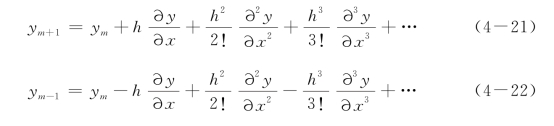
式中,h为选定的桩身增量长度。如果忽略上式中的高次项(3次以上),可以得到一次和二次导数中心差分的近似结果：

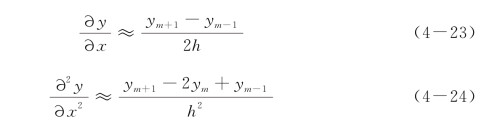
因此,这些表达式具有2次精度,要比采用“向前”或“向后”差分(1次精度)准确,即如果将桩身增量长度缩小一半,误差将近似降低4倍。因此,分段数量越多或h越小,解的精度就越高。由式(4-24)可进一步得到3次和4次微分的差分表达式：

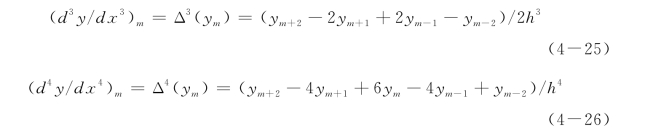
如果点m(深度xm)处变形为ym,惯性矩为Im,桩身材料弹性模量为Em,根据式(2-15)—式(2-18),则m点处的转角、弯矩、剪力和土体抗力为：

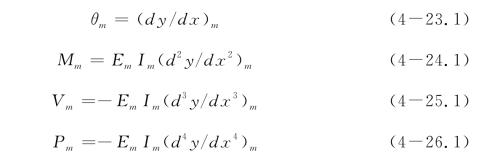
利用表达式(4-23.0)—式(4-26.0),式(4-23.1)—式(4-26.1)可表达为

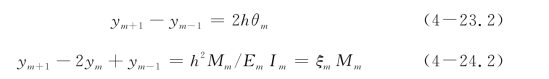
式中,ξm=h2/EmIm。

式中,ψm=-2h3/EmIm。

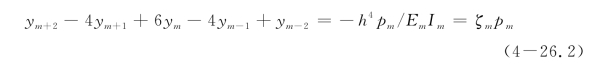
式中,ζm=-h4/EmIm。

参照Gleser(1984)对侧向受荷桩差分方法的描述,从桩端开始(m=0),可以得到桩头自由、完全固定或部分固定的差分方程,见表4-1。表4-1中包含t+4个方程,有t+5个未知数。第t+5个方程则可由桩头约束条件确定。

对于桩头自由桩(图4-3(a)),桩头弯矩为零,则有：

对于桩头固定桩(图4-3b),桩头转角为常数θt,即有：

表4-1　侧向受荷桩差分法统一方程(Gleser,1984)

如果桩头部分固定(图4-3(c)),即上部结构对桩头转动施加一定的约束Mt/θt(Mt=桩对上部结构施加的弯矩,θt=Mt引起上部结构的转角)(Reese&Van Impe,2001)已知,则有

式中,。桩头部分固定条件可以模拟刚性承台的转动或桩与承台接合处发生开裂后的桩基特性。

(2)土体抗力

由于采用理想弹塑性模型,土体抗力可表达为

式中,km=m点处的地基反力模量;yu(m)=m点处土体的屈服变形,等于pu(m)/km,pu(m)为m点处土体极限抗力。如果将式(4-26.3(m))右侧统一表达为

则有

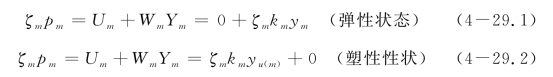
(3)差分方程的解

根据式(4-24.3(0)),式(4-25.3(0))和式(4-26.3(0)),消除y-1和y-2,并将y0表达为y1和y2的函数,有

式中

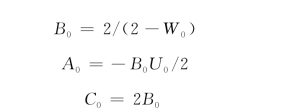
同样的,采用式(4-24.3(0)),式(4-26.3(1))和式(4-30(0)),可得

式中

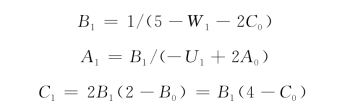
采用式(4-26.3(2)),式(4-30(0))和式(4-30(1)),可得

式中

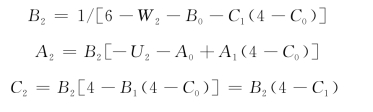
采用式(4-26.3(3)),式(4-30(1))和式(4-30(2)),可得

式中

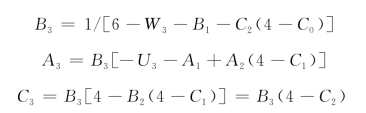
对于p≥m≥3时,按同样的方法,可得统一表达式：

式中

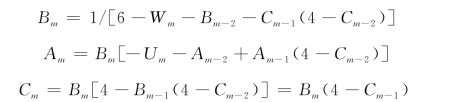
再将式(4-30(p)),式(4-30(p-1))和式(4-30(p-2))代入式(4-25.3(p)),得

式中(www.xing528.com)

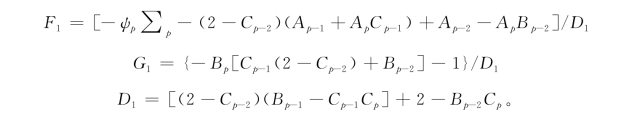
采用上述同样的方法,将式(4-30(p)),式(4-30(p-1))和式(4-31(1))代入式(4-25.3(p+1)),可得：

式中

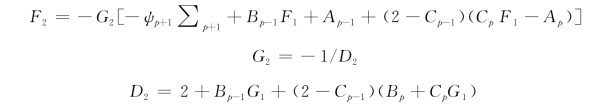
再由式(4-25.3(p+1)),式(4-30(p)),式(4-31(1))和式(4-31(2)),可整理得：

式中

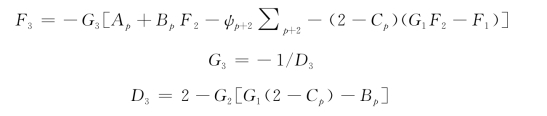
由式(4-25.3(p+3)),式(4-31(1)),式(4-31(2))和式(4-31(3)),可得：

式中

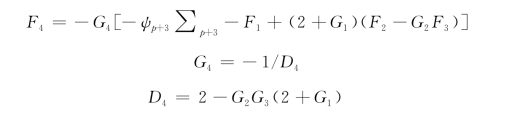
依此类推,对于p+4到点t,可得出统一的表达式：

式中

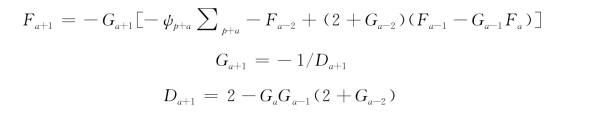
值得注意的是,上述方程对桩头自由、桩头固定和桩头部分固定的桩是相同的。三者的区别在于第t+5个方程,即约束方程不同。对于桩头自由桩,采用式(4-25.3′(t));对于桩头固定桩,采用式(4-24.3′(t));对于桩头部分约束的桩,采用式(4-27)。这些方程也可以表达为与yp+r+1,yp+r和yp+r-1的关系,其中,t=p+r。

参照Gleser(1984)相似的方法,首先推导r=0,1和2时桩顶约束条件的差分表达式,然后得出r为任意值的桩顶约束条件差分表达式。

①如果r=0

桩头自由

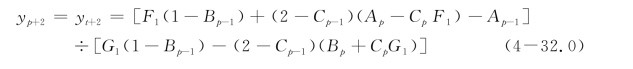
桩头固定

桩头部分固定

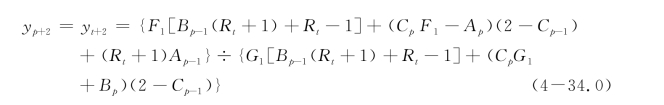
②如果r=1

桩头自由

桩头固定

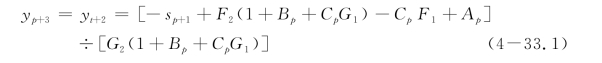
桩头部分固定

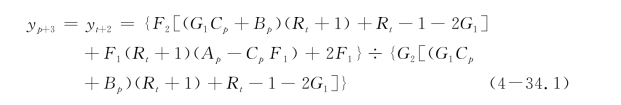
③如果r=2

桩头自由

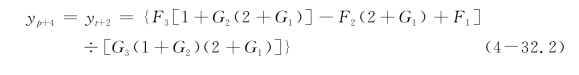
桩头固定

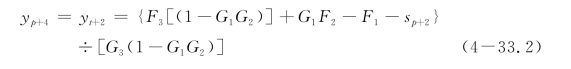
桩头部分固定

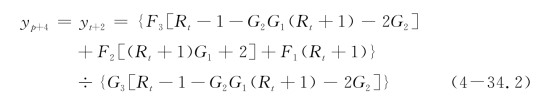
④如果r=r

桩头自由

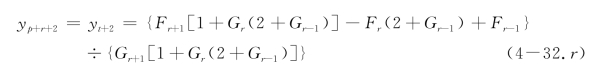
桩头固定

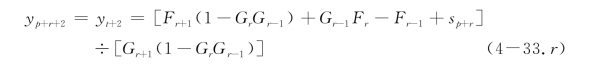
桩头部分固定

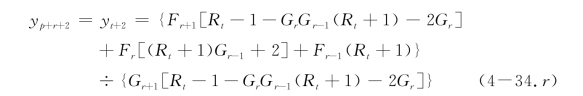
根据荷载大小、桩和土体参数,采用式(4-32.r)或式(4-33.r)或式(4-34.r)(r≥0)计算得到yt+2后,可以根据式(4-31(5))计算地面上各点的位移yp+a+1(0≤a≤r),即

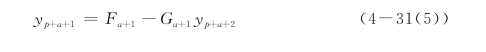
随后,采用地面上各点的位移与式(4-30(m))(3≤m≤p)计算第3点与地面之间各点的位移,即

然后,根据式(4-30(2)),式(4-30(1))和式(4-30(0)),分别计算第2,1和0点的位移。再将y2,y1,y0代入式(4-24.2(0)),可得到y-1：

最后将y2,y1,y-1代入式(4-25.3(0)),得到y-2：

在得到沿桩身各点的位移后,根据式(4-23.2)—式(4-26.2)分别计算各点的转角、弯矩、剪力和土体反力。

需要说明的是,如果在地面下一定深度内,存在与变形无关、沿深度分布的荷载q(如土体位移引起的极限土压力等),则可将该深度内的p-y曲线直接修改为(p-q)-y曲线。从而采用上述差分法统一求解。