锚锭板极限拉拔强度解析及应用探讨

(1)锚锭板极限拉拔强度上下限解

对于非均质黏土,土体不排水剪强度Su可假定沿深度线性变化,即

式中,Su0为地表处土体不排水剪强度;x为地面下土体深度;ρ为不排水强度沿深度增长的斜率(F/L3)。对于非均质土体中的平面锚锭板,如图3-11所示,其侧向抗拉强度qu可表达为(Merifield等,2001)：

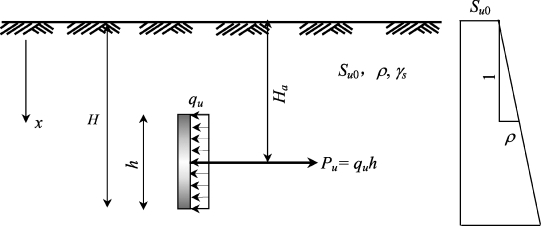
图3-11　黏土中侧向受拉锚锭板平面分析模型(Merifield等,2001)

其中,对于均质土体,即ρ=0,Su=Su0,

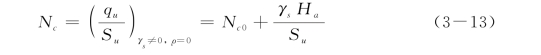
式中,Nc0为不考虑γs时的极限拉拔强度系数。对于非均质土体,即ρ≠0,

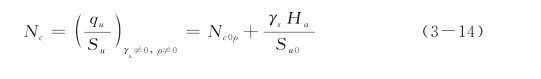
式中,Nc0ρ定义为

注意此时应将式(3-12)中的Su修改为Su0。

采用土体极限分析中的有限单元上下限解法(Sloan等,1988;Sloan &Kleeman,1995),Merifield等(2001)通过参数研究,给出了Nc0的拟合表达式：

和Nc0ρ的拟合表达式：

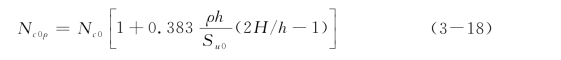
(2)不考虑γs影响时n与α0值

如果不考虑γs对锚锭板受拉强度的影响,将式(3-18)和式(3-14)代入式(3-11),得

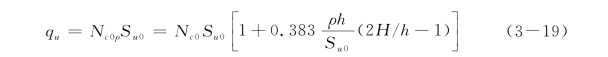
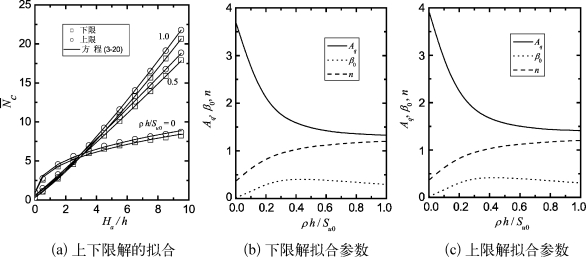
由于在侧向受荷桩的分析中,黏土的不排水剪强度一般采用5d深度内的平均值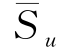,而不是地面处的不排水剪强度Su0。因此,将式(3-19)中的Su0替换为5h深度内的平均不排水剪强度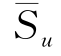,则有：

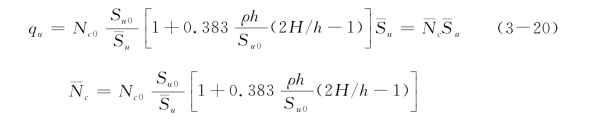
其中,Su0/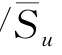=1/(1+2.5ρh/Su0)。式(3-20)可采用与桩的统一极限抗力式(3-3)相似的形式,即

或

进行拟合,其中Aq=锚锭板极限拉拔强度系数;β0=反映锚锭板在地面高度处极限拉拔强度大小的常数。对于ρh/Su0=0～1.0,拟合参数Aq,β0和n值如表3-8。图3-12给出了ρh/Su0=0,0.5和1.0时上、下限解的拟合曲线(图3-12(a))及相应的Aq,β0和n值与ρh/Su0的变化关系(图3-12(b),(c))。

(www.xing528.com)

图3-12　不考虑γs时上、下限解的拟合及其参数Aq,β0和n与ρh/Su0的关系

值得指出的是,对于ρh/Su0=0～1.0：①在地表处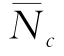=0.28～0.98,并随ρh/Su0值的增加而降低;②在5d深度下,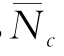可能大于深层绕流极限抗力系数(如式(3-1)中9～11.9),这是由于当ρh/Su0＞0时,Su沿深度增长,而本文仅采用5d深度内平均不排水剪强度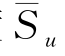的缘故。

表3-8　不考虑γs影响时锚锭板极限抗力的拟合参数

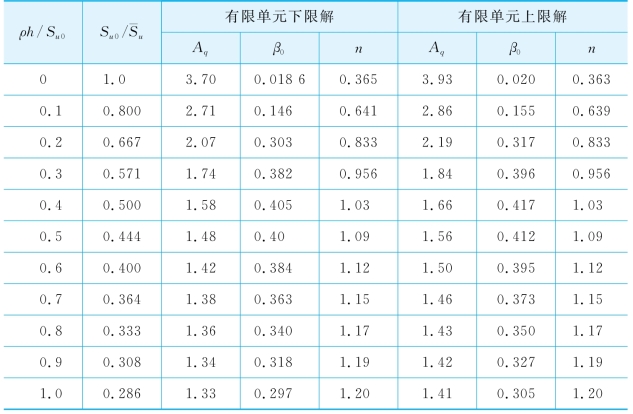
由图3-12(a)可见,对于上限和下限解,Aq,β0和n值的差别非常小,因此,该上、下限解可给出锚锭板极限拉拔强度较准确的解答。对于下限解,存在如下特性：①Aq值从ρh/Su0=0时的3.7陡降至ρh/Su0=0.4时的1.58,然后缓慢降低至ρh/Su0=1.0时的1.33;②n从ρh/Su0=0时的0.365增长到ρh/Su0=0.4时的1.03,然后十分缓慢地增长至ρh/Su0=1.0时的1.2;③β0从ρh/Su0=0时的0.02增长至ρh/Su0=0.4时的0.405,然后逐渐降低至ρh/Su0=1.0时的0.297。因此,ρh/Su0=0.4可能存在比较特殊的意义。我们认为,在ρh/Su0小于0.4时,锚锭板的破坏模式主要受Su0控制,此时n小于1.0;而ρh/Su0大于0.4后,ρx项控制锚锭板的破坏模式,表现出与砂土(锚锭板强度由γsx决定)相似的特性,因此n大于1.0。对于上限解,也表现出同样的特性,其中,Aq=1.41～3.93,n=0.363～1.20,β0=0.02～0.417。

对于低到中等塑性指数的黏土,Jamiolkowski等(1985)建议：

式中,OCR为超固结比。由式(3-10)和式(3-22)得

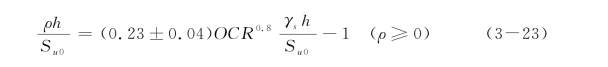
如果已知OCR,γs,Su0以及h,即可通过表3-8或图3-12得到相应的Aq,β0和n值。由于h值一般不是太大,对于常见的黏性土体,可能小于1,OCR=1～10(注意OCR大时值可能小,尽管二者没有确定的关系),则ρh/Su0通常小于0.4。在ρh/Su0=0～0.4时,Aq=1.58～3.93,β0=0.02～0.42和n=0.36～1.0,相应的平均值近似为2.8,0.22和0.7。

(3)考虑γs影响时的n与α0值

如果考虑γs对锚锭板受拉强度的影响,式(3-12)可表达为

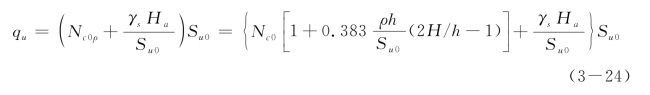
采用5h深度内的平均不排水剪强度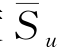,将式(3-24)改写为

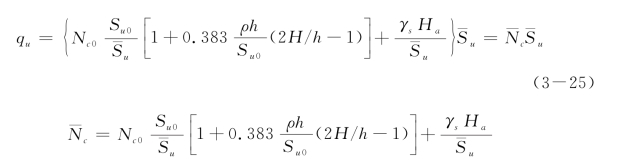
其中,Su0/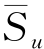=1/(1+2.5ρh/Su0)。同样地,式(3-25)可采用式(3-21)进行拟合。由于上下限解非常接近,表3-9只给出了ρh/Su0=0～0.5时下限解的拟合参数Aq,β0和n值。Aq,β0和n与ρh/Su0的变化曲线如图3-13所示。

由图3-13可见,对于ρh/Su0=0～0.5：①Aq值为1.49～4.98,随ρh/Su0和Su0/γsh的增加而降低;②β0值为0.02～0.4,随ρh/Su0的增加而增长;③在ρh/Su0≤0.1时,β0值随Su0/γsh的增加而降低;当ρh/Su0＞0.1时,β0值随Su0/γsh的增加而降低;④n=0.38～1.09,并随ρh/Su0的增加而增长。在ρh/Su0≤0.3时,n值随Su0/γsh的增加而降低;当ρh/Su0＞0.3时,n值随Su0/γsh的增加而缓慢增长;当ρh/Su0=0.3时,n值几乎不发生变化,近似为0.96。对于上限解,也表现出同样的特性,这里不再论述。

表3-9　考虑γs时土体锚锭板极限抗力下限解的拟合参数

图3-13　考虑γs时下限解的拟合参数Aq,β0和n值与ρh/Su0的关系

如果已知OCR,γs,Su0以及h,即可通过表3-9或图3-13确定相应的Aq,β0和n值。值得注意的是,由式(3-21)可知,在OCR值一定的条件下,ρh/Su0和Su0/γsh是相互制约的。当Su0/γsh值较大时,ρh/Su0较小,反之亦然。

对于ρh/Su0=0～0.4,Aq=1.59～4.98,β0=0.02～0.4和n=0.38～1.03,相应的平均值约为3.3,0.21和0.7。除了Aq较大外,β0和n平均值与不考虑γs时的结果十分接近。

黏土中侧向受荷桩与锚锭板的比较

对于黏性土,由于地面处土体极限抗力不为零,可将Ha视为深度x,则式(3-21)即为锚锭板极限拉拔强度沿深度的变化方程。

假定侧向受荷桩“单元锚锭板”(参考高度href=1,宽为桩径d)的极限压力与相同尺寸的实际锚锭板极限拉拔强度相等,即pu/d=qu,比较式(3-3)和式(3-20),则有相同的n值,并且Ng=Aqdn和α0=β0(L)。因此,在其他条件相同的条件下,桩径越大,Ng值越大(Stevens&Audibert,1979)。

综合上述在考虑和不考虑γs条件下对锚锭板拉拔强度的分析,当ρh/Su0=0～0.4时,n=0.36～1.03,Aq=1.33～4.98和β0=0.02～0.42。相应的平均值可取0.7,3和0.2。因此,对于黏土中的侧向受荷桩,可初步选取α0=0.2,n=0.7和Ng=3dn。考虑到沿深度方向上连续“单元”锚锭板之间的相互影响,Ng值应比3d0.7低。同时,由于施工扰动、表层裂隙黏土以及自由水的冲刷效应等,实际α0值也可能小于0.2。另外,应指出的是,上述锚锭板拉拔强度是通过锚锭板的平面极限分析得到的,而桩是三维结构,由于空间效应的存在,α0和Ng值也可能比上述值大。总之,α0和Ng值与特定的土体、桩基尺寸与施工方法、地下水埋藏深度等有关,不应也不可能给出一个固定的值。

另外,由锚锭板的极限拉拔强度分析可知,当ρh/Su0=0～1.0时,在地表处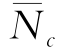=0.28～0.98,并随ρh/Su0值的增加而降低。因此,对于黏性土中侧向受荷桩的LFP,Ng0=0.28～0.98,并随ρ值的增长而降低。该Ng0值比Matlock LFP建议的3小,而R-C LFP建议的0.4接近于ρh/Su0=0.5对应的Ng0值。