土体极限抗力分布与侧向受荷桩性状

表3-1,表3-2和表3-3分别列出了不同研究者提出的砂土、Su-黏性土(土体强度采用不排水抗剪强度Su表征)和c-φ土体的极限抗力分布模式(以下简称LFP,Limiting Force Profile)。上述LFP可分为三类：①基于桩基现场试验资料得出的经验公式,如Broms(1964)和Barton(1982);②基于理论模型,再根据现场桩基载荷试验引入修正系数得到的半经验半理论公式,如Matlock(1970);Reese等(1974)和Reese等(1975);③根据桩周土体破坏模型得到的理论公式,如Hansen(1961)和Gluskov(1977)。

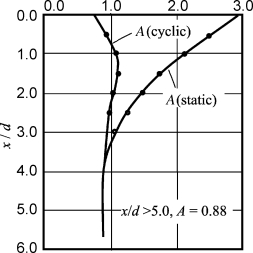
图3-5　R-S LFP极限抗力折减系数A

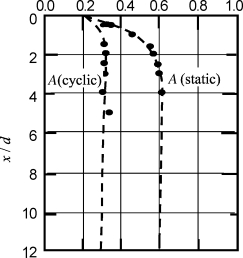
图3-6　R-C LFP极限抗力折减系数A

当砂土的内摩擦角φ分别为25°,30°和40°时,砂土的LFP比较如图3-7所示。由图可见：①归一化极限抗力pu/γsd2随φ的增长而显著增加。因此桩的施工、加密效应对LFP的影响不容忽视;②在2d深度内,Hansen LFP最小,Gluskov LFP最大;③当φ=25°时,在3d深度下,Gluskov最小,Barton LFP次之,Broms和Reese LFP较大;④当φ=30°时,在3d深度下,Gluskov最小,Barton与Barton LFP相同,Reese LFP最大;⑤当φ=40°时,在3d深度下,Broms和Gluskov LFP较小,Reese LFP较大。总体而言,Reese LFP最大,而Gluskov LFP最小。然而值得说明的是,表3-1和表3-2中的经验公式和半经验半理论公式都得到了一定数量的桩基现场试验验证,而Gluskov LFP的应用尚未见诸报道。因此,对于砂土中的LFP,主要对Broms LFP、Barton LFP和Reese LFP进行讨论。对于常见的砂土,内摩擦角φ=30°～40°,在上述三个LFP中,Broms LFP最小,Reese LFP最大。

表3-1　现有砂土的极限抗力

表3-2　现有Su—黏土的极限抗力

表3-3　现有c-φ土体的极限抗力

(www.xing528.com)

表3-4　O-G LFP折减系数(O'Neill&Gazioglu,1984)

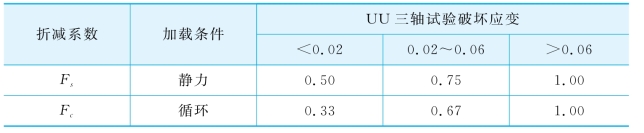
表3-5　Gluskov LFP折减系数(Gluskov,1977)

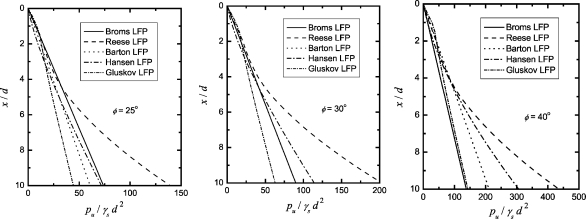
图3-7　砂土LFP的比较(γs=8.0 kN/m3,d=0.36 m)

当土体不排水剪强度Su=25 kPa,50 kPa,100 kPa时,10d深度内Matlock LFP(J=0.5)和R-C LFP的极限抗力分布如图3-8所示。同时,选取合适的土体c和φ值,使Hansen LFP接近Matlock LFP(J=0.5),并采用相同的c和φ值所得Gluskov LFP,也绘于图3-8中。由图可见：①不同的破坏模式确定的极限抗力分布不同;②在2d深度内,各LFP给出的土体极限抗力差别很大。如在地面处,Matlock LFP和R-C LFP给出的pu/Sud值分别为3和0.4,而Hansen和Gluskov LFP给出的pu/Sud值随Su值的不同而发生变化;③R-C LFP的归一化极限抗力pu/Sud几乎不随Su的变化而变化,而其他LFP的pu/Sud值则与Su有关。

图3-8　黏土LFP的比较(d=0.5 m)

无论对于砂土还是黏土,假设不同的破坏模式,将会得到不同的极限抗力分布。由于上部(2～7)d深度内的极限抗力对桩的性状影响显著,采用不同的LFP势必得到不同的桩基性状。这将在第4章中,根据侧向受荷桩的弹塑性解答作进一步分析。

在实际工程中,如下因素将影响极限抗力分布：①分层土体;②表层裂隙硬黏土的存在;③由于地下水的存在,浅层土体发生冲刷效应(Reese& Van Impe,2001);④桩的施工扰动对表层土体的影响(Mayne等,1995);⑤桩身的粗糙程度(Mayne等,1995);⑥循环荷载作用下,桩土界面间裂隙的形成或土体强度的软化(Randolph等,1988),等。然而,现有LFP都是基于相对均质土体、有限数量的小尺寸桩基现场试验结果,因此,在采用任何一种LFP时都应论证现场的土体、桩基和加载条件是否与推导该LFP的现场试验是否一致(Stevens&Audibert,1979;Guo&Zhu,2004)。