土体侧向受荷桩的极限抗力与性状

基于Vlasov双参数模型(Vallabhan & Das,1988,1991a,1991b),Sun(1994)提出了将土体视为各向同性弹性连续体的侧向受荷桩解答。对于长为L,半径为R,抗弯刚度为EI的圆形桩,如图2-12所示,桩周土体假定为理想均质、各向同性、线弹性材料,杨氏模量为Es,泊松比为νs。土体不受桩的影响,并且桩土界面之间不发生滑移。忽略由于侧向荷载引起的土体竖向位移ws,土体的侧向位移us和νs可表达为

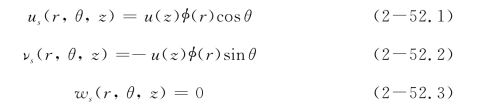
式中,u(z)为桩的侧向变形;φ(r)为无量纲函数,反映土体位移沿径向的变化。

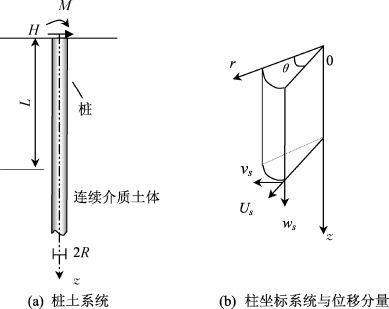
图2-12　桩与位移及应力柱坐标系统(Sun,1994)

以桩土系统作为研究对象,根据虚功原理,可推导得桩的变形控制方程为

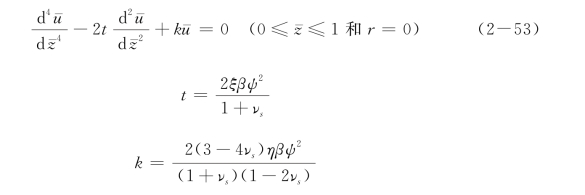
式中,β=Es/Ep;ψ=L/R;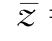=z/L,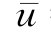=u/L;ξ和η与土体径向位移函数φ(r)有关;φ(r)由求解土体径向位移控制方程(由虚功原理得到)：

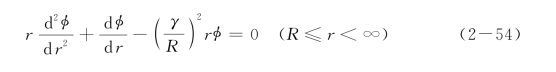(www.xing528.com)

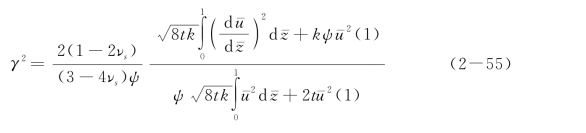
得：

则ξ和η可表达为：

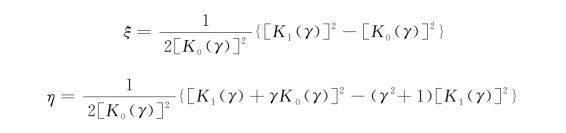
式中,Ki(γ)(i=0,1)为第二类i次Bessel修正函数。

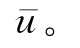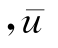结合桩的约束条件(桩头自由或固定,桩端自由或嵌固),Sun(1994)给出了式(2-53)的解不过与参数γ有关。同时由式(2-55)可知,参数γ亦为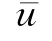的函数。因此,必须通过迭代过程求解参数γ,φ(r)及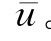。该迭代过程可参见Vallabhan&Das(1988)对双参数弹性地基梁求解方法的讨论。

与弹性地基梁法(将土体描述为离散的弹簧)比较,基于Vlasov模型的双参数法,能够考虑土体的连续性和弹簧间的相互作用。