土体极限抗力与桩性状计算

对于桩的基本微分式(2-13),如果采用弹性地基梁法求解,则解答与地基反力模量相关;如果采用弹性连续体法求解,则其解答与土体的弹性模量有关。通过比较两者的解答,可建立地基反力模量与弹性模量之间的理论关系。

Biot(1937)推导了三维弹性半空间上无限梁在梁中集中荷载作用下的解答。他发现,如果令弹性连续体理论与弹性Winkler地基梁理论产生的最大弯矩相等,得到k和Es如下关系：

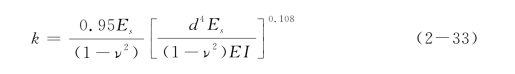
Vesic(1961)将Biot的解答扩展应用于三维弹性半空间上无限梁在梁中受集中荷载和集中弯矩的情况,并令弹性连续体理论与弹性Winkler地基梁理论产生的转角相等,得到k和Es如下关系：

因此,选定的比较标准不同(最大弯矩或转角),将得到不同的k值。另外,由式(2-33)和式(2-34)可以发现,对于圆形或方形桩,k值与桩的尺寸无关(Terzaghi,1955;Watkins&Spangler,1958)。

由式(2-33)和式(2-34)的推导过程可知,弹性Winkler地基梁理论与弹性连续体理论只满足选定的比较标准(最大弯矩或转角),并不能保证土体内的应力和变形相一致。Guo&Lee(2001)假定桩周土体位移场的分布形式与弹性有限元法分析得到的位移场一致,采用变分法推导了均质、各向同性土体的地基反力模量k为

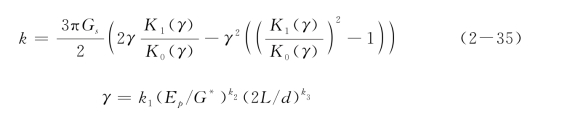
式中,γ为荷载传递系数;Ep为等效实心桩杨氏模量,EI/(πd4/64);G*为等效剪切模量,=(1+0.75νs)Gs;νs,Gs分别为土体泊松比和剪切模量;k1,k2,k3为计算常数,与桩型、桩头荷载、桩头和桩端约束有关,如表2-10所列。

表2-10　荷载传递系数γ的参数(Guo&Lee,2001)

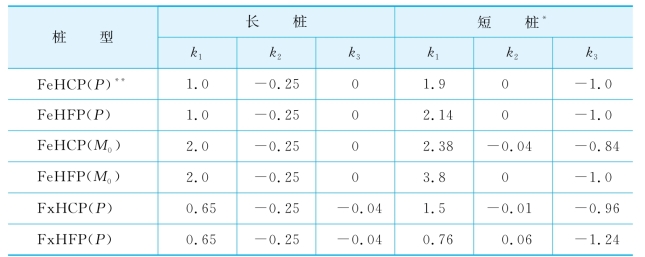
*：如果Ep/G*≤(Ep/G*)c,则为长桩,否则为短桩。对于Fe HCP(M0)和Fx HFP(P),临界刚度(Ep/G*)c应替换为4(Ep/G*)c。
**：Fe H=桩头自由桩,CP(P)或CP(M0)=水平荷载P或弯矩M0作用桩端嵌固桩;FP(P)=水平荷载P或弯矩M0作用摩擦桩;Fx H=桩头固定桩。

式中,Ki(γ)为改进第i次第二类Bessel函数(i=0,1),可近似表达为

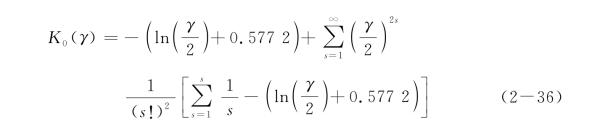
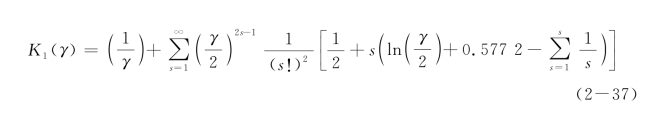
一般的,上式中的前三项就可以给出足够准确的结果。Guo和Lee在推导弹性地基反力模量过程中,不仅满足桩土交界面处的位移条件,而且还满足土体内的应力条件。

另外,通过比较弹性地基梁解答与弹性有限元分析结果,也可得到地基反力模量与土体剪切模量之间的关系。Randolph(1977)采用有限元方法结合傅立叶级数技术,对侧向受荷桩进行了弹性分析。在该方法中,桩土系统离散为轴对称环形单元,而不对称荷载可采用傅立叶级数转化为对称荷载和反对称荷载。具体的分析过程可参见相应的文献。由于该方法能够准确地模拟圆形桩,往往能够得到比偏微分方程积分法更准确的解答(Randolph,1977)。Randolph(1977)采用该方法得到均质弹性土体中柔性桩(包括桩顶自由和桩顶固支)的性状,并得到了偏微分方程积分法(Poulos,1971a)和其他有限元方法(Kuhlemeyer,1979a,1979b)的验证,计算精度在10%以内(Randolph,1981)。根据大量的参数研究,桩顶变形和转角可采用代数表达式拟合如下(Randolph,1981)：

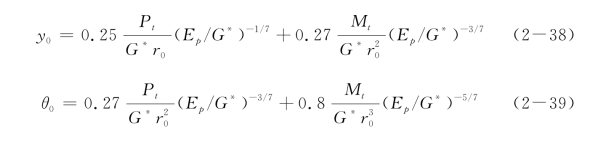
式中,r0为桩半径(对于空心桩,则为外径);并且桩的有效长度可表达为

如果采用弹性地基梁法求解式(2-13),Hetenyi(1946)给出了地面处受侧向荷载Pt和弯矩Mt作用、k为常数的柔性桩桩头位移和转角：

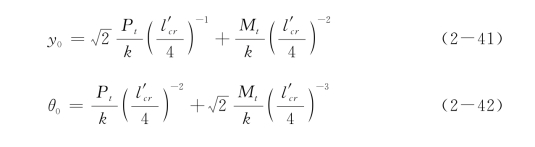
式中,桩的有效长度为(www.xing528.com)

如果令式(2-38)和式(2-41)产生的桩顶位移或式(2-39)和式(2-42)产生的桩顶转角相等,可得到地基反力模量与土体剪切模量之间的关系。分析过程如下：

(1)假定由式(2-40)和式(2-43)得到的有效长度相等,即l′cr=lcr,则可用式(2-40)代替式(2-43),采用式(2-41)计算桩顶位移。在只有水平荷载Pt作用,令式(2-38)和式(2-41)得到的桩顶位移相等,可得到地基反力模量k与土体等效剪切模量G*存在如下关系：

将式(2-44)代入式(2-41),结合式(2-40),可得l′cr=1.026 6lcr。该值与假定的l′cr=lcr不一致。重新假定l′cr=1.026 6lcr,按上述方法可得k=11.02G*(Ep/G*)-1/7和l′cr=1.033 4lcr。该值与假定的l′cr=1.026 6lcr仍有一定的差别。重复上述过程,迭代计算直到假定的和计算的l′cr与lcr关系一致,即有l′cr=1.035 6lcr,此时有：

(2)同样,假定l′cr=lcr,如果只有弯矩Mt作用,令式(2-38)和式(2-41)得到的桩顶位移相等或只有Pt作用,令式(2-39)和式(2-42)得到的桩顶转角相等,可得k=14.815G*(Ep/G*)-1/7,比较式(2-43)和式(2-40)得l′cr=0.96lcr。重复上述过程,迭代计算直到假定的和计算的l′cr与lcr关系一致,即有l′cr=0.921lcr,此时有：

(3)在只有弯矩Mt作用下,比较由式(2-39)和式(2-42)分别得到的桩顶转角,重复上述分析过程,可得

式(2-46)和式(2-47)计算的k值非常接近,分别为式(2-45)所得k值的1.47和1.53倍。考虑只有弯矩Mt作用下k值的唯一性,式(2-46)和式(2-47)得到的k值应该相等,因此在弯矩作用下可取式(2-46)和式(2-47)的平均值,即

因此,只有弯矩作用下的地基反力模量约为只有水平荷载作用下地基模反力模量的1.5倍。在图2-1中,如果只有水平荷载作用在地面高度时,采用式(2-45)计算地基反力模量;当只有弯矩作用时,采用式(2-48)计算地基反力模量;当水平荷载作用在地面上一定高度时,地基反力模量为式(2-45)计算值的1～1.5倍。上述计算k值的方法简称“本文方法”。

对于常见的桩土相对刚度,即Ep/G*=102～105,则由式(2-45)可得到k/Gs=7.4～2.4。相应的,由式(2-48)得到k/Gs=11～3.6。由k/Gs=2.4～11,可进一步得到k/Es≈0.8～4.6。k/Es值基本上覆盖了表2-6给出的α经验值。由于桩土相对刚度越大,k/Gs值越小,表2-6中α较大值适用于桩土相对刚度较小(柔性桩)的情况,反之亦然。同理,对于文献报道的k,kh或nh经验值,较大值可能适用于柔性桩,而较小值适用于相对刚性桩。值得注意的是,尽管上述k值的计算公式由均质土体分析得到,但对于分层土体或土体剪切模量沿深度发生变化的土体,可近似采用各层土体的剪切模量按本文方法计算各层土体的地基反力模量。对于黏性土,刚性系数Ir=16～500(图2-9),则k/Su为38～5 500;对于砂土,Gs≈(0.2～0.64)NSPT(MPa),NSPT为标准贯入击数,可得k≈(0.5～7)NSPT(MPa)。

以桩的长径比为25,土体泊松比为0.5为例,比较式(2-33)、式(2-34)、式(2-35)、式(2-45)和式(2-48)得到的地基反力模量,如图2-11。其中,P表示在地面处只有侧向受荷作用,M表示只有桩头弯矩作用。

根据图2-11,可得到如下结论：

(1)只有弯矩作用时(如Guo(M)或本文(M))的地基反力模量是只有侧向受荷作用时(Guo(P)或本文(P))的地基反力模量的1.1～1.5倍。

(2)对于相对柔性桩,k值较大;对于相对刚性桩,k值较低。k值随桩土相对刚度的增长而不断降低,但降低的幅度逐渐减小,并最终趋于常数。

(3)与Guo&Lee法比较,Biot和Vesic法给出的k值偏低,而本文方法得到的k值偏高。本文方法偏高的原因主要是由于有限元分析过程中采用轴对称环向单元(未考虑桩与桩后土体之间的拉裂),导致土体刚度的增加。

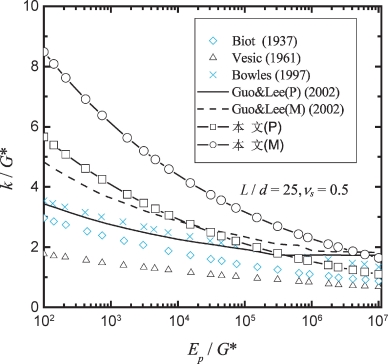
图2-11　不同地基反力模量公式的比较

因此,在侧向受荷桩的分析中,可采用式(2-35)确定地基反力模量。当采用本文方法确定地基反力模量时,应除以系数1～1.5。对于桩土相对刚度较大的侧向受荷桩,除以较小的系数;对于桩土相对刚度较小的桩,则除以较大的系数。这样,上述两种方法将给出非常一致的结果。采用Guo&Lee法比较准确,但采用本文方法可以直接手算,避免采用Bessel函数。对于常见的侧向受荷长桩,即Ep/G*=103～104,可将本文(P)的计算结果除以系数约1.3得到k值。