土体极限抗力与侧向受荷桩性状-kh经验数值与计算式

对于水平或竖直梁,Bowles(1988)给出了计算地基反力模量的统一表达式：

式中,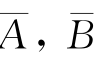为地基反力模量计算常数;x为水平梁埋置深度或竖直梁地面下研究点的深度。因此,对于地面上宽为B的梁,竖向地基反力系数kv由连续基础的极限承载力(qult)得

假定极限承载力对应的梁的变形为y=25.4 mm,则

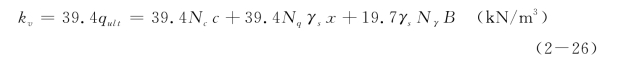
对于无黏性土,c=0,则

比较式(2-24)和式(2-27),可得：

采用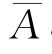,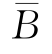和n,可以得到变形为25.4 mm对应的竖向地基反力系数kv。根据Francis(1964)的建议,考虑侧向剪切阻力的影响,侧向地基反力模量可取竖向地基反力模量的两倍,因此：(www.xing528.com)

式中,kh为侧向地基反力系数。

采用与Bowles相似的方法,Audibert& Nyman(1977)建议采用下式计算侧向受荷桩的地基反力系数：

式中,σx为深度x处的上覆压力;Nq为承载力系数,由下式确定：

式中,A为与内摩擦角、给定位移有关的常数;d为桩径。根据试验资料,当内摩擦角为30°时,A值如表2-7所列。在较大变形条件下,Nq趋近于一个极限值。

表2-7　A值(Audibert&Nyman,1977)

以x/d=1为例,由表2-7和式(2-31)可得,kh(y=2.54 mm)=6σx/y和kh(y=25.4 mm)=16σx/y,后者是前者的2.7倍。值得注意的是,kh(y=12.7 mm)并不接近于kh(y=2.54 mm)和kh(y=25.4 mm)的平均值,而是接近于kh(y=25.4 mm)。这说明较小的变形增量将导致地基反力系数(或模量)较大幅度的降低。

因此,当采用弹性地基梁法分析侧向受荷桩时,由于桩的侧向变形沿深度降低,应将桩分为若干部分,每部分将赋予与变形水平相对应的kh值,即上部对应于变形较大值的kh值,而下部对应于较小变形对应的kh值。因此,采用沿深度增长的地基反力模量(Davisson&Gill,1963;Randolph,1977)或与变形相关的地基反力模量(如kubo,1965;Matlock,1970;Reese等,1974)比采用常数k更合理。