土体极限抗力与侧向受力桩特征

根据桩长对侧向受荷桩性状的影响,侧向受荷桩可分为刚性桩(或短桩)和柔性桩(或长桩)。如果桩的埋置深度小于有效桩长,为刚性桩;反之,为柔性桩。有效桩长定义为：超过有效桩长的部分对桩顶的性状不产生或产生可忽略的影响。有效桩长的确定往往根据经验方法或通过数值模拟得到半经验半理论的解答,典型的确定方法如表2-2所示。

表2-2　有效桩长的计算

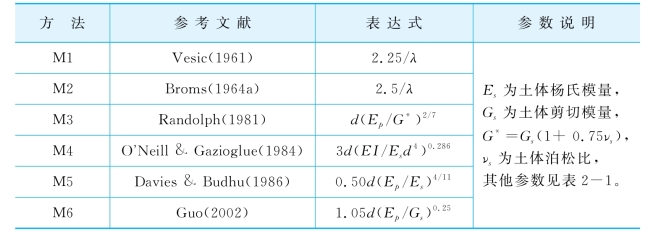
计算分析表明,对于常见的桩基,除了M5确定的有效桩长偏小外,其他方法给出的结果差别不是太大。通常在M1,M2和M6确定的有效桩长以下,桩的变形已可忽略不计而桩身弯矩还存在一定的值;而在M3和M4确定的有效桩长以下,桩的变形和弯矩都可忽略不计。因此,本文采用方法M3计算有效桩长,即

对于常见的侧向受荷桩,桩的等效模量Ep为104～105MPa。土体剪切模量Gs值为1～100 MPa,泊松比为0.2～0.4,则根据式(2-19),Lcr为4～25倍的桩径。黏土越软或砂土越松而桩的刚度越大,Lcr值越大;反之,Lcr值越小。对于一般的岩石,Gs值的数量级为102～104MPa,泊松比为0.1～0.35,则Lcr为1～7倍的桩径。靠近岩面的岩石越软或风化程度越高而桩的刚度越大,Lcr值就越大。

因此,在侧向受荷桩的分析过程中,主要讨论Lcr深度内的土体参数。当然,Lcr值又与选取的土体模量有关。这可通过简单地试算确定,即先选取一定深度内(如对于土体取10d,对于岩石取6d)的平均Gs值,计算Lcr值;若Lcr值与选取的深度相差较大,可再选取该步所得Lcr深度内的平均Gs值,重新计算新的Lcr值;重复该过程直至平均Gs值对应的深度与计算得到的Lcr值接近为止。

柔性桩和刚性桩往往表现出不同的破坏模式(Fleming等,1992;Broms,1964a,1964b)。对于桩头自由的刚性短桩,如图2-5所示,桩的破坏将以地面下桩身某点为中心,整体发生转动,转动中心离地面的高度一般为70%～80%的桩基嵌入长度(Fleming等,1992)。对于桩头自由的柔性长桩,如图2-6所示,其破坏模式主要表现为土体破坏或在最大弯矩发生深度(或剪力为零)xmax处出现塑性铰破坏(如果桩截面沿深度不变)。对于桩头固定的侧向受荷桩,如图2-7所示,随桩长的不同,主要表现为三种破坏模式,即短桩整体平移,长桩双塑性铰(分别发生在桩头最大负弯矩和桩身最大正弯矩处)破坏,以及介于二者之间的中间破坏模式,即桩头首先出现塑性铰,随后桩绕某深度处发生整体转动。(www.xing528.com)

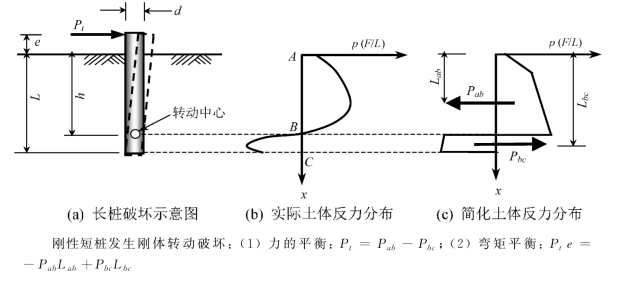
图2-5　桩头自由刚性短桩破坏机理(Fleming等,1992;Broms,1964a,1964b)

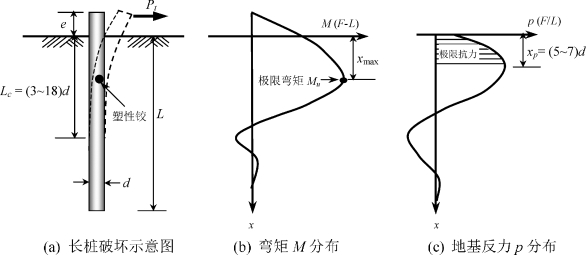
图2-6　桩头自由柔性长桩的破坏机理(修改自Fleming等,1992;Broms,1964a,1964b)

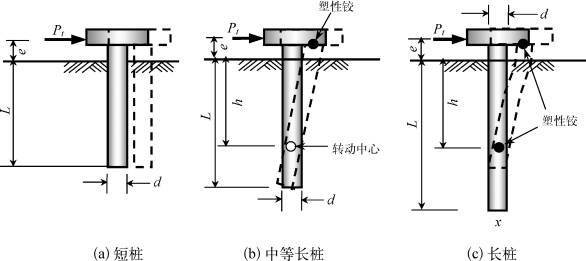
图2-7　桩头固定桩的破坏机理(Fleming等,1992;Broms,1964a,1964b)

对于刚性桩的设计,主要采用传统的极限荷载法(如Broms,1964a,1964b;桩基工程手册,1995)确定极限承载力。如图2-5所示,假定土体极限抗力的分布,根据力和弯矩的平衡,即可确定桩顶的极限荷载。对于柔性长桩极限承载力的计算,一般假定塑性铰以上的土体抗力(塑性铰以下的土体抗力自相平衡),根据力和弯矩的平衡确定桩顶的极限荷载。然而,目前常用的土体抗力分布模式(Broms,1964a,1964b)并没有得到理论和实践的论证。并且,除了允许大变形桩或相对短桩外,侧向受荷桩的设计往往由桩的侧向变形控制(Poulos&Hull,1989)。通常情况下,在水平荷载还没有达到极限承载力时,桩的变形可能已超过了允许变形。因此,桩的极限承载力通常定义为一定的桩顶变形(如10%d或20%d)对应的侧向荷载,而不是真正达到塑性破坏时的荷载大小。另外,对于柔性长桩,极限承载力也只有通过考虑土体的荷载传递规律,才能准确地确定最大弯矩的发生位置以及该深度内的土体抗力分布,进而确定相应的最大弯矩。

因此,变形分析和极限荷载设计本质上是统一的,后者只是前者的“塑性极限”状态。然而,现有的设计方法往往将二者分开考虑(如Fleming等,1992),前者大多采用弹性Winkler地基梁法,而后者基于假定的土体极限抗力分布,由力的平衡法确定。因此,有必要发展侧向受荷桩的弹塑性解答,不仅要准确预测变形,而且能够准确确定桩的最大弯矩和极限承载力。