行星轮系传动比变化对转向有巨大影响

图8-46a所示为一平面行星轮系，由于轮系中行星轮的轴线不固定，其传动比不能直接用定轴轮系传动比的计算公式来计算。可应用转化轮系法，即根据相对运动的原理，假想对整个行星轮系加上一个绕主轴线O-O转动的公共转速-n_H。显然轮系中各构件的相对运动关系并没有改变，但此时行星架H的转速变为了n_H-n_H＝0，即相对静止不动，它支撑的行星轮也变为轴线不动的定轴齿轮。于是原来的行星轮系便转化成为一个假想的定轴轮系，如图8-46b所示，这个转化所得的假想定轴轮系称为原行星轮系的转化轮系。轮系中各构件转化前后的转速如表8-6所示。

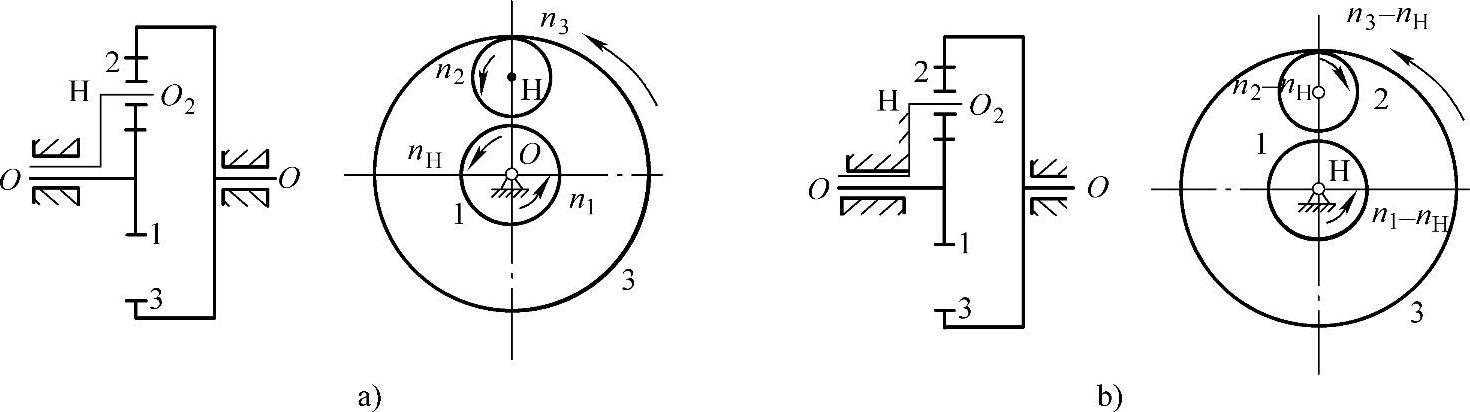
图8-46 行星轮系及转化轮系

表8-6 转化轮系前后转速对比

既然转化轮系是一个定轴轮系，就可以应用定理轴轮系传动比的计算公式求其中任意两个齿轮的传动比。转化轮系中齿轮1和齿轮3的传动比为

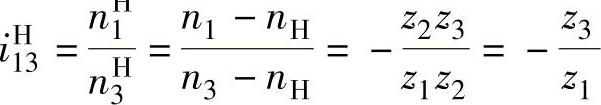
符号中右上角标“H”，表示转化轮系传动比或转速相对行星架H的值。推广至一般情况

式中，下标1为首轮，k为末轮。

使用式（8-39）时应特别注意：

1）齿轮1、齿轮K与行星架H三个构件的轴线必须相互平行，否则不能应用该式。

2）将n₁、n_k、n_H的值代入上式计算时，必须带正负号。对差动轮系，如两构件转向相反时，将其中一构件的转速用正值代入，另一构件的转速则用负值代入，第三个构件的转速用所求得的正负号来确定。

3）i_1k≠i^H_1k，i_1k是行星轮系中齿轮1和齿轮K的传动比，而i^H_1k是该行星轮系的转化轮系传动比。

例8-4 图8-47所示为一行星减速器中的轮系，已知各齿轮齿数为z₁＝100，z₂＝101，z₂′＝100，z₃＝99，试求传动比i_H1。(www.xing528.com)

解：图示行星轮系中齿轮1为活动太阳轮，齿轮3为固定太阳轮（即n₃＝0），双联齿轮2-2′为行星轮，H为行星架。其传动比的计算可由式（8-39）得

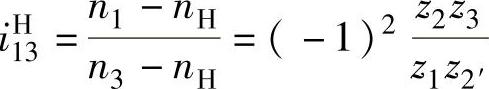
将n₃＝0代入上式，得

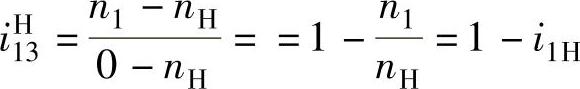
则

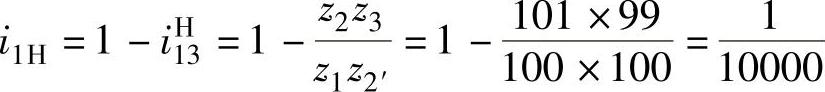
即

i_H1＝10000

这说明当行星架H转10000转，齿轮1才转1转，且两构件转向相同。本例说明行星轮系只用少数几个齿轮就能获得很大的传动比。

若将z₃的齿数由99改为100，则

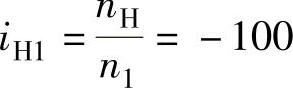
若将z₂的齿数由101改为100，则

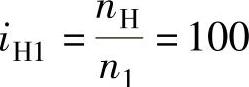
由此可见，同一种结构形式的行星轮系，由于某一齿轮的齿数略有变化，其传动比就会发生巨大的变化，同时转向也会改变。