凸轮机构从动件的运动规律

凸轮机构能否按预期的运动规律正常工作，主要取决于凸轮的轮廓曲线，加工凸轮的依据就是确定凸轮的轮廓曲线。

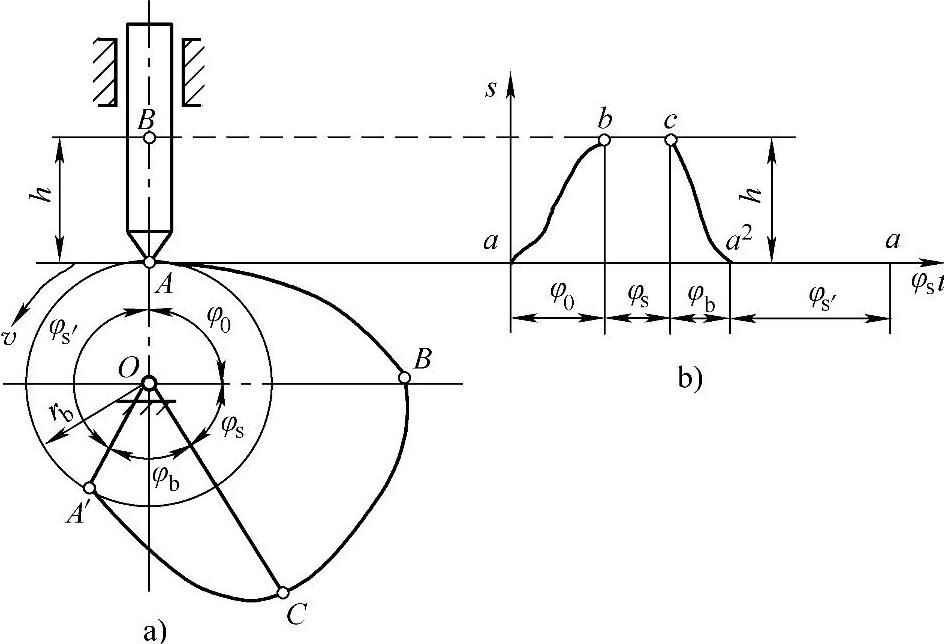
图7-35 凸轮与从动件的关系

1.凸轮轮廓曲线与从动杆运动的关系

通常，主动凸轮等速转动，从动杆做往复移动或摆动。从动杆的运动直接与凸轮轮廓曲线上各点向径的变化有关，而轮廓曲线上各点向径大小又是随凸轮的转角而变化，这种关系称为从动杆的运动规律。根据运动方程或运动线图，即可绘制出凸轮的轮廓曲线。

在如图7-35所示的尖顶移动从动杆盘形凸轮机构中，以凸轮轮廓最小半径r_b为半径的圆称为基圆，r_b称为基圆半径。设计凸轮轮廓曲线时，应首先确定凸轮的基准圆（基圆）。在图示位置，尖顶与凸轮轮廓上的A点（基圆与轮廓AB的连接点）相接触，此时为从动杆上升的起始位置。当凸轮以ω逆时针方向回转一个角度φ₀时，从动杆被凸轮轮廓推动，以一定的规律，由起始位置A到达最高位置B，这个过程称为从动杆的升程，它所移动的距离称为行程，而与升程对应的转角φ₀称为升程角。凸轮继续回转φ_s时，以O为中心的圆弧BC与尖顶接触，从动杆在最高位置停歇不动，称为远停程，角φ_s称为远停程角。凸轮继续回转φ_h时，从动杆以一定的规律回到起始位置，这个过程称为回程，角φ_h称为回程角。凸轮再回转φ_s′时，从动杆在最近位置停歇不动，称为近停程，角φ_s′称为近停程角。当凸轮继续回转时，从动杆重复上述运动。

如图7-35b所示，将凸轮的转角φ与从动件的位移s的关系用曲线表示，此曲线称为从动件的位移曲线，即s-φ曲线。从图7-35b中看出，从动件的位移s是随凸轮转角φ_s′变化的，也是随时间变化的。因此当凸轮以等角速ω转动时，从动件的位移s、速度v和加速度α的变化规律，都是由凸轮轮廓决定的。

2.等速运动规律（直线运动规律）

当凸轮以等角速度回转时，从动杆在升程或回程的速度为一常数，这种运动规律称为等速运动规律。

如图7-36所示，分别以从动杆的位移s、速度v和加速度a为纵坐标，以凸轮转角φ（或时间t）为横坐标，作s-φ、v-φ及a-φ线图。由于速度v为常数，所以速度曲线为平行于横坐标轴的直线。位移曲线为斜直线，故这种运动规律又称为直线运动规律。因速度为常数，故加速度为零。然而，在行程开始位置，速度由0突变为v，其加速度为无穷大。同样，在行程终止位置，速度由v突变为0，其加速度也为无穷大。在这两个位置，由加速度产生的惯性力在理论上也突变为无穷大，致使机构发生强烈的冲击，称为刚性冲击（实际上由于材料的弹性变形，加速度和惯性力不会达到无穷大），所以，等速运动规律只能用于低速、轻载和特殊要求的凸轮机构中。

3.等加速等减速运动规律（抛物线运动规律）

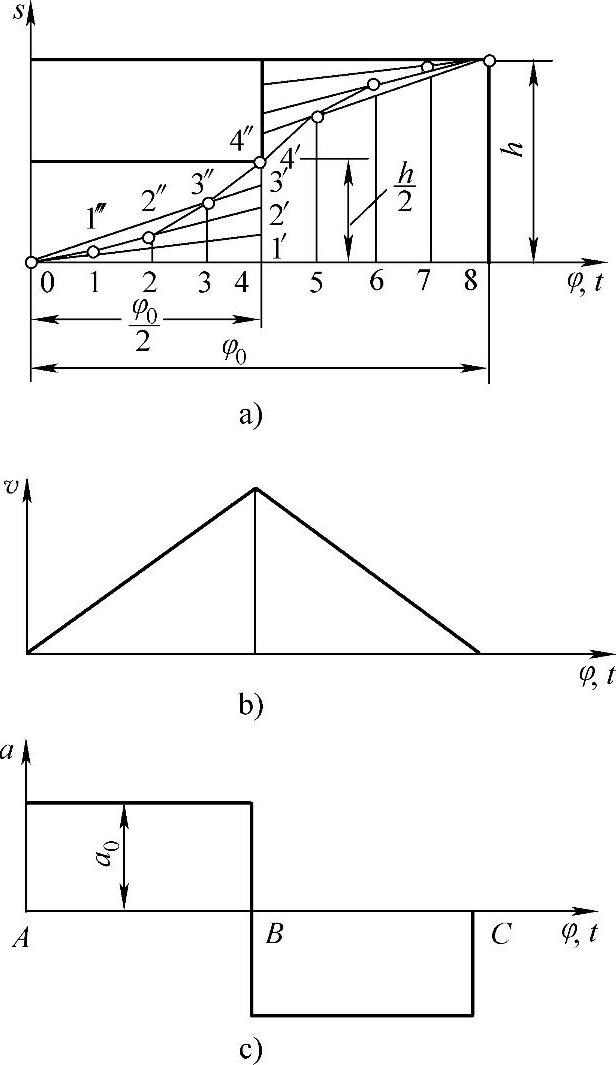
这种运动规律是从动杆在一个升程或回程中，前半段做等加速运动，后半段做等减速运动，通常加速度和减速度的绝对值相等。

如图7-37所示，这种运动规律的位移曲线由两段光滑相连的抛物线所组成，故这种运动规律又称为抛物线运动规律。由图可见，等加速等减速运动规律当有远停程和近停程时，在升程和回程的两端及中点，其加速度仍存在有限突变，惯性力将为有限值，由此而产生的冲击称为柔性冲击。因此，等加速等减速运动规律只适用于中速、轻载的场合。

4.余弦加速度运动规律（简谐运动规律）

如图7-38所示，这种运动规律的加速度是按余弦曲线变化的。加速度曲线是余弦曲线，速度曲线是正弦曲线，而位移曲线是简谐运动曲线，故这种运动规律又称为简谐运动规律（质点在圆周上做等速运动，它在这个圆的直径上的投影所构成的运动为变速运动，称为简谐运动）。由加速度曲线可见，这种运动规律在升程或回程的始点和终点，从动杆有停歇时（停程角不为零），该点才有柔性冲击。如果从动杆做无停歇的往复运动（停程角为零），加速度曲线变成连续的余弦曲线，运动中可以消除柔性冲击，在这种情况下，可用于高速的场合。

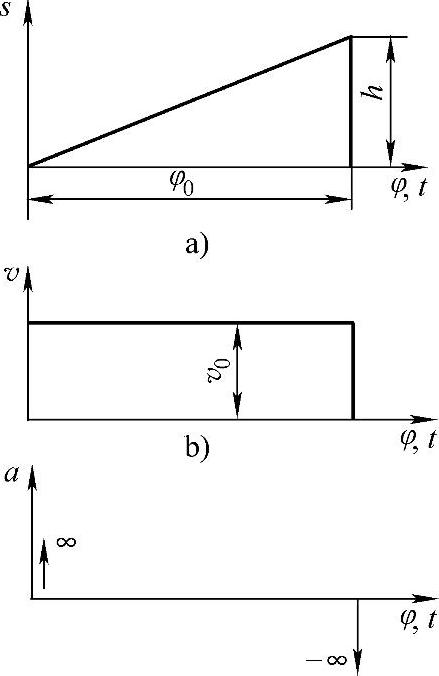
图7-36 等速运动规律

(www.xing528.com)

图7-37 等加速等减速运动规律

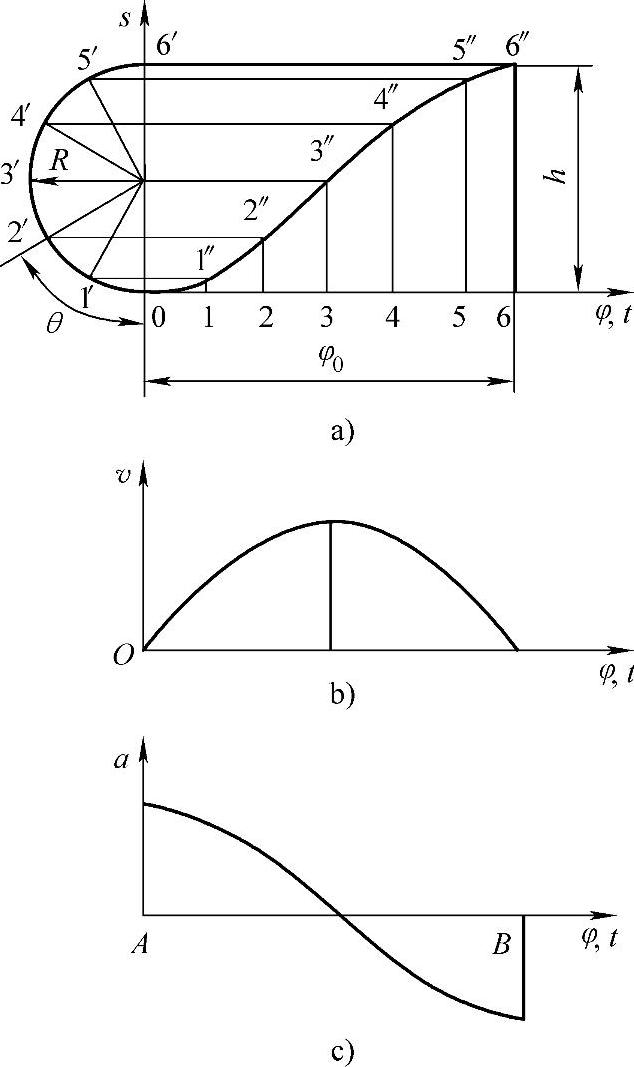
图7-38 余弦加速运动规律

5.凸轮轮廓曲线的几个参数

（1）压力角的概念 如图7-39所示，凸轮机构在升程的某个位置，不计摩擦时，凸轮作用于从动杆上的推力F_n将沿接触点B的法线方向。作用力F_n与从动杆速度v所夹的锐角称为凸轮机构在图示位置的压力角。显然，压力角α越大，推动从动杆运动的有效分力F_y＝F_ncosα越小，分力F_x＝F_nsinα越大，由此引起导路中的摩擦力阻力越大。当压力角α达到某一数值时，有效分力F_y已不能克服由F_x所引起的摩擦阻力，于是无论力F_n多大，也不能使从动杆运动，从而出现自锁。为了保证凸轮机构正常工作，并具有较高的传动效率，必须限制凸轮的最大压力角不得超过许用值[α]。对于移动从动杆凸轮机构，升程中，[α]＝30°；回程中，[α]＝70°～80°。

（2）凸轮机构的压力角与凸轮基圆半径的关系 在图7-40中，凸轮与从动杆在任意点B接触时，设从动杆的速度为v₂，凸轮B点的速度为v₁，则

v₂＝v₁tanα＝rωtanα（7-4）

而凸轮在B点的向径r＝r_b+s。凸轮机构的最大压力角发生在从动杆速度最大的位置，此时的基圆半径为最小值。所以设计时的最小基圆半径（mm）为

为保证凸轮机构正常工作，应取凸轮基圆半径（mm）为

式中，s为从动杆在最大速度时对应的位移，单位为mm。

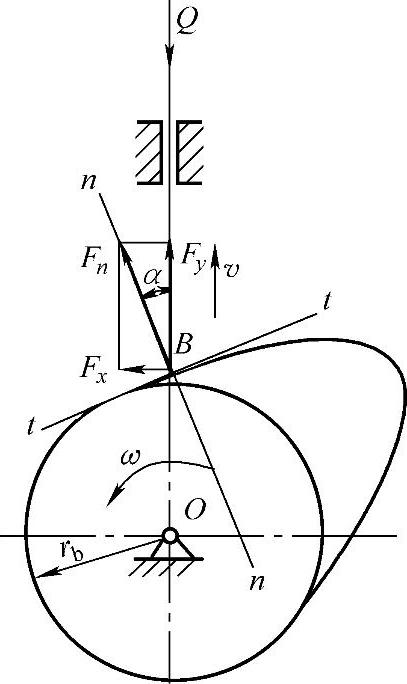
图7-39 凸轮机构的压力角

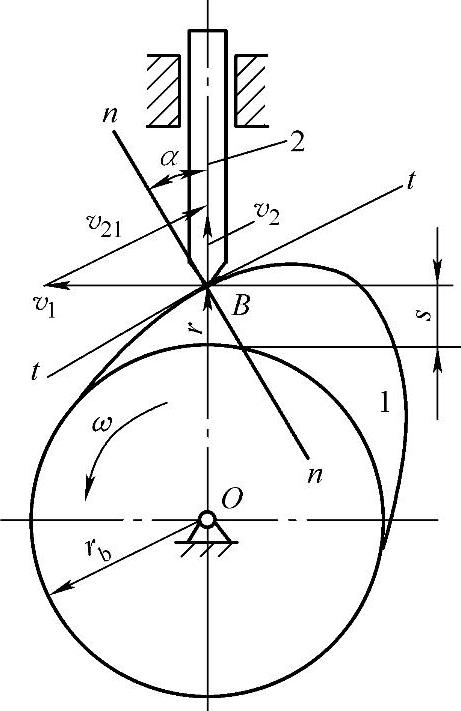
图7-40 压力角与基圆半径的关系