汽车机械基础：转矩计算方法

扭转是杆件变形的另一种基本形式，其受力表现为在垂直于杆件轴线的两个平面内，分别作用有大小相等、方向相反的两个力偶矩，变形表现为任意两个横截面发生绕轴线的相对转动。工程中通常把以扭转为主要变形形式的杆件称为轴。

使杆件产生扭转变形的外力偶矩用m表示。它一般可通过力的平移并利用平衡条件确定，也可由轴所传递的功率P（单位：kW）和轴的转速n（单位：r/min）计算，其计算公式为

现以受两外力偶矩m作用下的圆轴为例，如图2-4a所示，分析扭转时的内力。由截面法，在n-n处假想地将轴分为两部分，取左段Ⅰ为研究对象，如图2-4b所示。根据平衡条件，可知截面上存在一个与外力偶矩m大小相等、方向相反的力偶矩，这个力偶矩就是杆件受扭转时横截面的内力，称为转矩，用T表示，即

T＝m （2-6）

如考察右段Ⅱ的平衡，如图2-4c所示，仍可得到T＝m的结果，但T的方向与由左段Ⅰ求出的相反。为使不管取轴段Ⅰ或Ⅱ为研究对象所得的同一截面上的转矩不仅数值相等而且符号相同，将转矩T的符号规定如下：若按右手螺旋法则把T表示为矢量，当矢量方向与截面的外法线方向一致时，T为正；反之为负。按照这一规定，在图2-4中，无论对轴段Ⅰ或Ⅱ，截面n-n上的转矩都是正的。

当作用于轴上的外力偶多于两个时，可用图线表示沿轴线各截面上转矩的变化情况，这种图线称为转矩图。下面举例说明转矩图的画法。

例2-2 传动轴如图2-5a所示。主动轮A输入功率P_A＝36kW，从动轮B、C、D输出功率分别为P_B＝P_C＝11kW，P_D＝14kW，轴的转速为n＝300r/min，试作轴的转矩图。

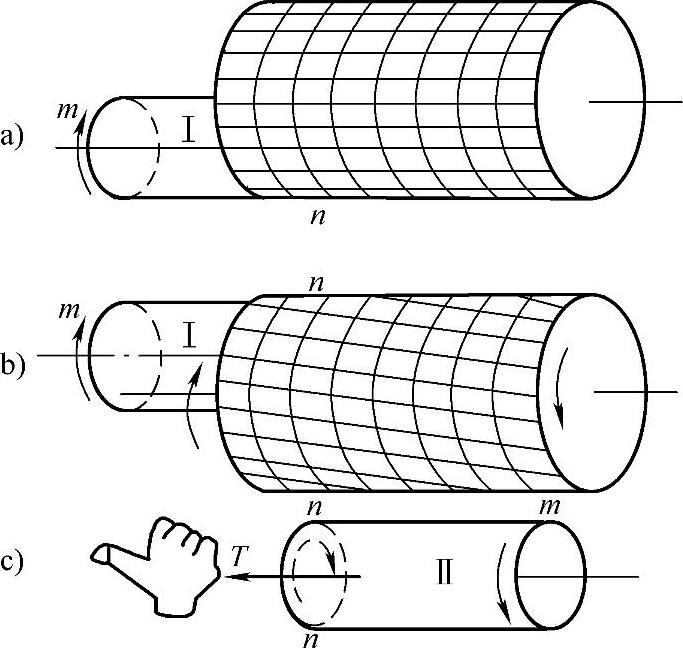
图2-4 圆轴扭转时转矩计算简图(www.xing528.com)

图2-5 传动轴的转矩计算

解：由式（2-5）算出作用于各轮上的外力偶矩分别为

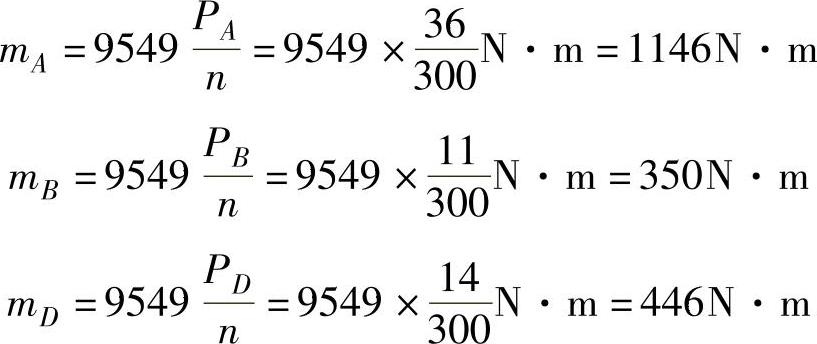
由截面法，在图2-5b中，由∑m＝0知

T₁＋m_B＝0，即T₁＝-m_B＝-350N·m在图2-5c中，由∑m＝0知

T₂＋m_B＋m_C＝0，即T₂＝-m_C-m_B＝-700N·m在图2-5d中，由∑m＝0知

T₃＝m_D＝446N·m

轴的转矩图如图2-5e所示。