在中国古代,虽然早就有“两小儿辩日”之争,以及时而见于记载的个别学者对此现象的探索,但基本都局限在对太阳大小的解释上。从整体上看古人作的目视观天的尺度记录,看不出古人自觉认识到这种视错觉的普遍存在,就更不知道在记录中有意校正之了。也就是说,古人的那些记录应该都是包含着扁平天穹视错觉数据在内的,这就需要我们对这些数据进行校正和重新归算,这应是一项很有意义的工作。
那么对“扁平天穹”理论,下一步要做的就是从“量”的方面探讨这个错觉的天穹到底扁平到什么程度,因为有了定量的标准,才可以对古代记录的相关视错觉进行校正和归算。
关于人们感觉到的天穹究竟扁平到什么程度,前人做过不少实验观测,也建立过非常简单的量化模型。测试数据表明,天穹的扁平程度是可以度量的,而且随着昼夜的不同、晴阴的不同,天穹的扁平程度也有着不同的大小。一般来说,目视天穹阴天比晴天扁平,白昼比夜晚扁平,有月的夜晚比无月的黑夜扁平——这说明,“大气消光效应”说也是不能完全排除的,至少它可以造成天穹扁平度的变化。
为了定量表示天穹的扁平程度,如图4.4.1所示,我们作出半个天穹,O 为观测点。当天穹为半球形时,天顶到地平的弧线为ZH0;当天穹为扁平弧形时,天顶到地平的弧线为ZH1、ZH2等等。
我们把这些弧线的中点M0、M1、M2找出来,把它们分别与O 点相连,连线与水平线的夹角分别为α0、α1、α2,显然,随着天穹扁平程度的不同,α0>α1>α2。
由于这个角α 可以作为衡量天穹扁平程度的一个醒目量值,本书称它为“视扁度角”。从图中可知,天穹为半圆形时,α=α0=45°,天穹愈扁,α 角愈小。
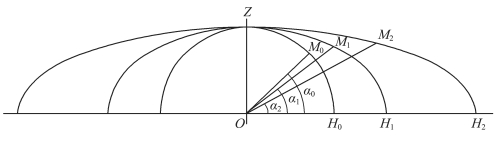
图4.4.1 天穹的视扁度角
由许多学者在不同地区、不同时间、不同天空亮度下的观测统计结果得知,α 角介于20°到40°之间。笔者综合这些结果,选定无月晴夜、有月晴夜、曙暮薄明、白昼晴天、白昼昙天5种情况的视扁度角如下:
无月晴夜 α=40°
有月晴夜 α=36°
曙暮薄明 α=34°
白昼晴天 α=32°
白昼昙天 α=26°
这5种情况不但可以涵盖所有天文观测记录,亦可用于气象及其它天空现象记录的数据校正。关于“昙天”,从天空多云难见阳光到阴云密布都可以看作昙天。至于“阴夜”的情形,有月、无月效果一样,更看不到其它天象,其它大气光象以及不明飞行物也很难看到,所以这里不予讨论。
有了具体的度数,我们再来解释一下视扁度角α 在目视观测中的含义:当我们用肉眼估计好距地平45°的高度角的位置后,再用仪器测量该点,发现此角比我们估计的要小得多,在无月晴夜,它为40°,有月晴夜为36°,等等。
我们以太阳为例:太阳的视大小从地平到天顶是连续变化的,那么必定有一个高度,太阳的“视大小”与“真大小”相同。我们可以把这个高度的太阳当作“标准大小”,以此为标准,对其它高度的太阳“视大小”进行量化分析。
按照这种方案,笔者建立了一个合理的校正归算模型,用内插法得出一系列不同高度太阳“视大小”的值,惊奇地发现这个不发生畸变的位置并不是视扁度角高度,而是另一个角度,笔者为它取名为“标准高度”,用β 表示。在上述5种天空情况下,通过计算可求出对应的标准高度如下:
无月晴夜 α=40° 标准高度β=43°
有月晴夜 α=36° 标准高度β=41°
曙暮薄明 α=34° 标准高度β=40°
白昼晴天 α=32° 标准高度β=39°
白昼昙天 α=26° 标准高度β=37°
我们可以举白昼晴天的情形为例说明。如图4.4.2所示,半圆弧为目视天球,它仍为半球状,扁弧形为发生错觉时的视天穹,它与目视天球相交于真高度39°处(由于目视观测的复杂性,这个图仅是示意说明)。也就是说,当太阳真高度为39°时,太阳光盘的视直径等于其“真”角直径;真高度低于39°时,我们估计的太阳光盘的角直径就会过大,越近地平线越大;高于39°时,对太阳光盘视直径的估计就会过小。按古人的说法,高度39°处的太阳被形容为“大如碗”(古代碗的平均大小约为古尺半尺,恰为半度),而天顶的太阳被形容为“大如盏”,地平线上的太阳则“大如盘”。这个模型与古人的说法相符。
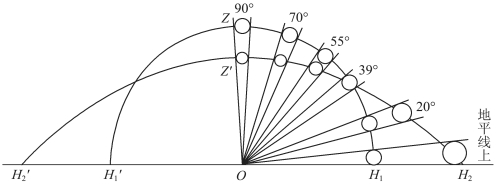
图4.4.2 晴昼时在扁平天穹上估计太阳大小的错觉(数字为真高度)
我们再看一下扁平天穹视错觉误差对天体视地平高度的影响。举晴朗月夜为例,如图4.4.3所示,从观测者O 出发,在目视天球上每5°作一小扇形(数字沿圆弧连续标出),它们表示每增加5°的高度在观测者眼中张开的视角。这每5°角本来是相等的,但它们与扁平天穹所交截的视弧却大不相同,在近天顶的部分与天穹截交的视弧很小(3°左右),而在近地平的部分与天穹所截交的视弧则很大(7°左右)。扁平天穹上的视地平高度数字沿扁弧分两段标出。(https://www.xing528.com)
这样我们就可以直观地得出,在晴朗月夜时,地平高度10°的星体,人们会估测为15°左右;地平高度45°的天象,则会估为54°,等等。
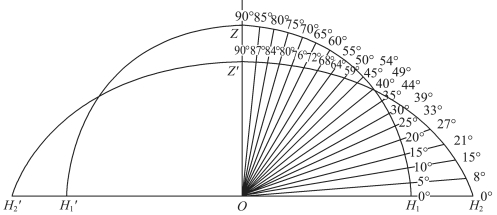
图4.4.3 晴朗月夜时人们在扁平天穹上估计地平高度的错觉示意图
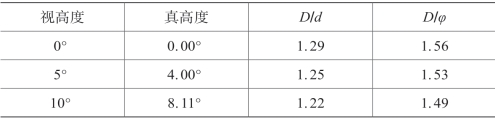
以前述5种情况的视扁度角α 为基本参数,用内插法,可以得出各种情形下的一系列校正表,见下面的表4.4.1~表4.4.5,表中D 为有视面天体(如日、月)在某高度的视角直径,d 为有视面天体在“标准高度”的视角直径(可称为“标准直径”),φ 为有视面天体在天顶的视角直径。这些表格将5种天空情况下人们目视天空时的错觉以精确量化的方式表示出来,在使用古代有关的天象记录时,天体的视大小、角距、长度都要按这些表格进行校正归算。5 种天空情况的具体含义如下:
①无月晴夜:即所谓“月黑夜”,很多夜间天象记录都是在这种情形下观测的,均需用表4.4.1。晚上、黎明前有亮度很小的新月或残月时也要用此表。月全食时,照度非常低,也可认为是无月晴夜。②有月晴夜:除新月和残月外,只要是能引起“月明星稀”效果的晴夜,均需用表4.4.2。天上(全天或部分)有薄云,可见月晕、月华时,亦用此表。另外,处理大火流星的记录时,因天空亮度较高,也要用此表。③曙暮薄明:白天黑夜间的晨昏曚影阶段用表4.4.3。④白昼晴天:日出和日落之间的晴日白昼(含日出、日落过程)用表4.4.4。天空半阴半晴的情形也用此表。天空布满薄云,但有较明显的日光时,按气象惯例仍视为晴天,故日晕等现象仍用此表。⑤白昼昙天:天空多云难见阳光直到阴云密布时都可用表4.4.5。用于一些特殊天气现象、云下空中现象的观测。
有的读者可能会怀疑,本书第一部分重复刘次沅的工作,统计对照史书中的行星掩、犯、合的记录值与推算值,得出1尺=1°的结论时,并没有考虑扁平天穹的视错觉啊!实际上我们是考虑过天象的地平高度的,试图发现随着天象地平高度的减低其估测尺度增加的情况,但最后发现二者没有明显的相关性。其原因可能是:记录行星掩、犯、合是一种很特殊的观测活动,多数情况下只注意角距很近的情况,所选恒星为固定的几十颗,观测时与某些恒星间的角距直接比较即可较客观地估出相对距离;至于月亮与行星恒星的掩、犯、合,更可以用月亮的直径(半尺)为标尺作出准确估计,这样扁平天穹的视错觉就不起主要作用了。另外,无月的夜间天穹扁平程度较小,错觉也较小,很近角距的估测可能会被随机误差掩盖。也幸而这类记录避免了明显的视错觉,才使前辈学者直接统计即得出了1尺=1°的结论。
表4.4.1 无月晴夜时(α=40°)天穹天体高度与大小校正表
(续表)

表4.4.2 有月晴夜时(α=36°)天穹天体高度与大小校正表
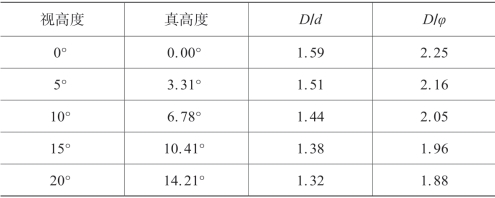
(续表)
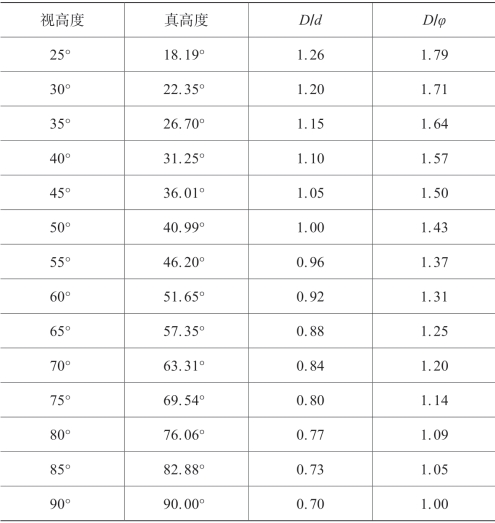
表4.4.3 曙暮薄明时(α=34°)天穹天体高度与大小校正表
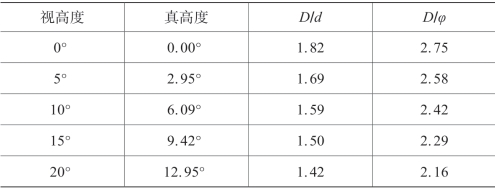
(续表)
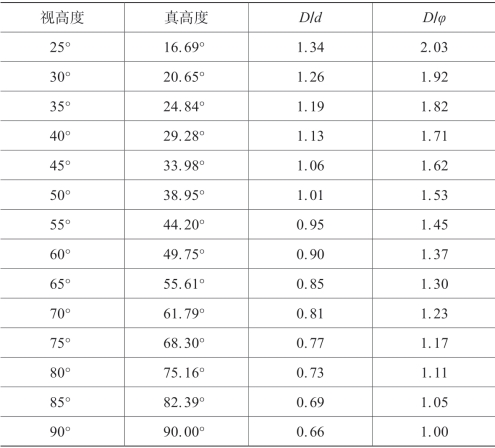
表4.4.4 白昼晴天时(α=32°)天穹天体高度与大小校正表
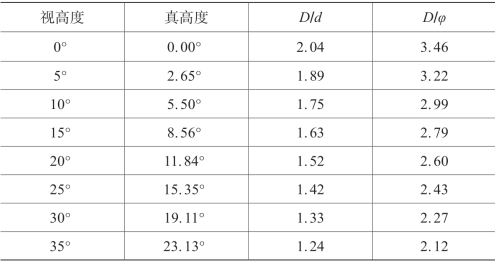
(续表)
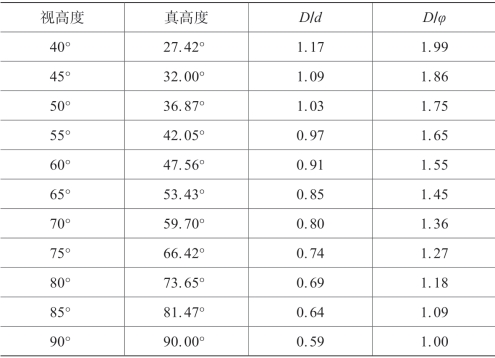
表4.4.5 白昼昙天时(α=26°)天穹天体高度与大小校正表
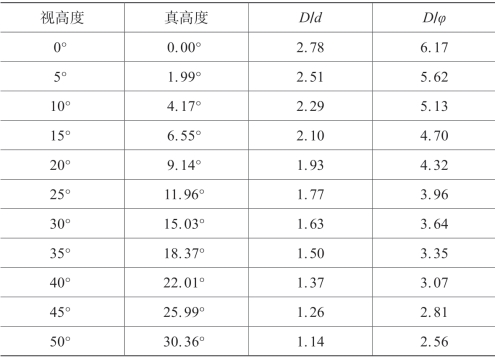
(续表)
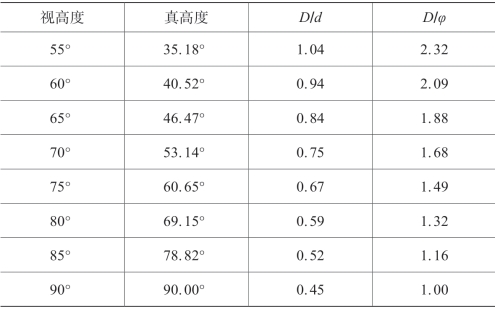
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




