古代天文观测：目视尺度与心理渊源

前面曾多次提到“立体视觉”，那么立体视觉到底在尺度记录体系里扮演的是什么角色？下面我们专门探讨这个话题。

前面，我们早就得出了“1尺=1度”的换算关系，这个关系是那么简洁、完美、顺理成章，但它在古人那里究竟是怎么得来的，我们还需要探索一番。前文我们曾举出《周髀算经》中记载的测二十八宿距度的方法来说明，那么古人测天尺度体系标准的设立，就是为了这种测度术的划分方便而偶然选定“1尺=1度”的吗？不是的。《周髀算经》中的事例只是一条说明古代人把尺与度联系起来的证据，并不是尺度体系参照系建立的源头，尺度体系参照系的建立是有着更为深刻而复杂的原因的。

我们在前文还提到，古人在进行目视天象观测时，是不会同时作着“1尺=1度”换算的。但建立了尺度体系的13米半径的天球模型后，是不是可以说，古人（也包括今人）观天时，他们都时刻自觉地想到五六丈开外有一层水晶壳般的天球面，然后把所有的天体现象都换算成这个球面上的投影来估测度量呢？也不能这样说，因为我们查遍元、明时代以前的典籍，连1尺=1度的换算关系都找不到，更何况什么“目视天球”“投影”之类的痕迹了。看来实际情况是这样的：古人虽然是在这种天球模型的意义上做着具有一定精度的天文测量工作，但他们大抵并无明确的自觉，更不会有58尺半径的“天球”和换算成“投影”这类概念，对他们来说估测过程包含的都是些“意会知识”或“未说出的知识”。观测者很可能是凭借他们代代相传的经验、共识、个人的悟性以及本能，在下意识的层面来直接估算的。

笔者之所以说古人是在下意识的层面“选定”目视观天时假想天球的大小来估算，是因为这个过程可以归结到一种人本行为的模式，其中人的进化本能、立体视觉、生活经验和心理习惯起到了决定性的作用。

这里简单介绍一下在天文观测中目视观测的特殊性。目视观测不需要借助任何设备，只需无近视、散光等视力缺陷的人站在观星台上或任意视线不受遮挡的地方用肉眼直接观看天象并估测即可。其优点是视野开阔^[1]、响应灵敏、估算迅速、使用方便，所以直到今日，在流星和极光观测时，目视手段也是不可缺少的。它的不足之处是估测时误差较大，精度难以保证，有视错觉现象，观测者的心理状态不佳与训练水平不高还会使误差进一步加大。

单从心理状态上看，肉眼直接观测与仪器观测也是很不同的。用仪器观测时，哪怕是用很简单的观测仪器如窥筒，人的观测行为也会机械地归结为一套客观被动的记录程序；而目视观测时，人需要调动整个视知觉参与，视知觉统率观测的全部，因此目视观测就不简单地是一个被动的记录过程了。首先，在目视观测天象时，视野中星体的亮度、颜色、相互（角）距离、长度、大小、运动等，其状况的确定很大程度上要依赖于观测者的生活经验，体现出观测者的主体性；其次，由于视野异常宽广，观测对象与参照物之间对比的影响就变得十分突出；第三，目视观测时，观测者的大脑还会以其知识背景为基础，对所看到的天象进行概括和联想，因此会导致一些特有的观测结果；第四，有时观测者心中的预期也起着作用，甚至观测者能感知到一个熟悉的对象的另一种不同的面貌；最后，目视观测时几乎总是双眼共用，而双眼是会产生立体视觉效果的，虽然人观看遥远的天体时不可能出现立体视觉，但日常生活中的立体视觉习惯会不知不觉地左右着人们的目视天象观测。

人总把“天”想象为覆盖在头顶上的“天穹”，而古人作天象投影估测的“天幕”半径是13米。这个13米半径的投影天幕不可能就是人们想象的那个“天穹”，因为地面上的景物，我们常常一望就能望出去几百米、几千米甚至更远（如几万米外的远山），笼罩大地这些景物的天穹当然也是同样巨大的。所以，这13米半径的天幕一定有另外来源。

人类确立半径13米的假想天球，在视知觉的种种因素中，人的立体视觉起着至关重要的作用。

某些哺乳动物如马、羊、兔子等，它们的双眼长在头的两侧，双眼的视野完全不重叠，这类动物仅有单眼视觉。而人的双眼则都在头部的前方，相距约65毫米，大部分视野是相互重叠的，重叠视野范围内的任何物体都能同时被两眼看见，这时两眼视网膜上各形成一个完整的物像。由于眼外肌的精细协调运动，可在主观上产生单一物体的视觉，并产生被视物体的厚度以及深度或距离等感觉，这称为立体视觉。虽然借助单个眼球运动、生活经验、物体光照也能产生一些立体视觉，但立体视觉主要还是由这种双目视差产生的。

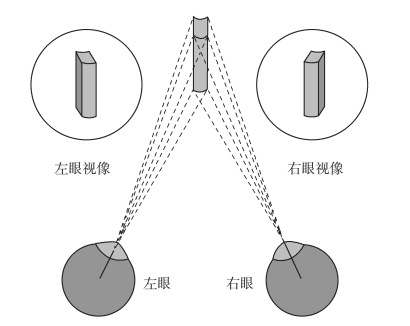
图3.1.1　双眼视差产生立体视觉示意图(www.xing528.com)

人为什么具有立体视觉？人类学家认为，人的立体视觉是灵长类动物为适应树栖而进化形成的。灵长类动物大多数生活在树上，需要不断在丛林树枝间跨来跨去，而跳出去抓握住几米、十几米外的树枝是必须要有良好的立体视觉的，这样才能精确地估算出树枝的距离以便抓握。食肉动物像猫、虎的眼睛也在前面，有很强的立体视觉，这也是为了便于准确捕食而进化的结果。而食草动物如马、羊、兔子等，只需要警惕敌害出现而迅速逃跑，所以眼睛为两侧分布，视野极宽但几乎无立体视觉（称为立体盲）。

与食草动物相比，立体视觉使人的视野变窄，但使视觉质量大大提高。靠立体视觉，在日常活动中我们可以准确地判断身边物体的距离；再远一些时，我们也可以凭借双眼视差大致判断两个物体的相对远近；在有大量参照物可资对比时，这种判断相对远近的能力可延伸到很远的距离。

但是，据视觉生理学家的研究，在均一的背景下（如观察天空时），立体视觉的距离则是非常有限的。实验证明，在均一的背景下，当一个物体离开人10米以上时，如果没有相邻事物作参照，对于一个形状简单、颜色单一的物体，受试者往往讲不出它们的确切距离是多少。

既然人的立体视觉来自树栖祖先估测距离的需要，那么从“精确地估测距离”的意义上来说，树梢的高度以及在树间可跳越的最大距离就应是树栖祖先精确估测距离的极限。人类显然也保留了这个能力，十余米正是人们日常生活中所遇树梢的平均高度，所以13米可看作目视时不会引起显著的双眼视觉的最小距离，于是人在下意识中把这个距离选作观天、测天的最佳参照距离。

所以，目视观测天球尺度的选定，可以说根据的是以人的本能、经验为标准的选择原理，可称为“天穹估测的人择原理”。从某种意义上说，这是一种“集体无意识”，其最佳值为约13米。

视觉生理学有一术语为“明视距离”，指在合适的照度下，人眼近看目的物时的最佳距离。实验早已证明，人眼的明视距离为25厘米，也就是说，正常的人眼在合适照度下观看此距离处的物体时十分舒适，最不费力。当人用放大镜、显微镜观察物体时，由于看物清晰，眼球不必刻意调节，在这种舒适状态下，人总把物体想象为是在25厘米之外的“明视距离”处。

通过上面的分析可以得出结论，人眼远看目的物时也有一种“明视距离”，其距离值是13米。人们目视观天时，这种“明视”效果更为明显，因为这时光线来自极远处，眼球更不必去刻意调节，感觉很舒适，所以人的本能总把天象（包括大气光象）想象为是在13米外的“明视距离”处，然后按日常经验来估测其大小和角距。为此我们可以得到一个新概念：人眼的远距明视距离——13米。

关于这个问题，德国心理学家威廉·冯特有一段论述可以参考：

如果我们通过一根管子窥视月亮，或者从手指合拢的缝隙间观看月亮，我们只见到月亮所在的那部分天空，月亮的大小不会超过半个克朗（crown，英国旧制5先令硬币——译注），可是一般看来月亮大约有盘子那么大。对这一事实的简单解释是，我们现在并没有把月亮定位在树林背后的某个地方（树林占据了我们正常视野的前景部分），而是把月亮定位在管子后面的某个地方，或者手指合拢后面的某个地方。同样，当我们用普通望远镜观察月亮时，月亮看上去较小，不比通常见到的更大，尽管望远镜把东西放大了，而且我们可以在望远镜的帮助下看到月亮表面上的一些东西，这些东西是肉眼看不见的。这也是因为月亮并未被定位在某个距离上，而是被定位在望远镜的另一端。

有了13米半径目视天球，我们可以进一步解释：人们抬头看到的月亮如“盘子那么大”，是因为人看到的是整体的天穹；当通过管子、指缝、望远镜观看月亮时，就没了整体目视天穹的知觉，所以“13米半径目视天球”就不起作用了。

总括而言，尺度体系中的13米半径假想天球主要来自人类视知觉的行为和心理因素。在中国古代目视观天的尺度体系中，目视天球才是本原的东西，是尺度体系的真正支柱，而1尺=1度的换算关系仅仅是表层的现象，是13米半径假想天球推出的一个结果。而且，一尺恰好等于一度只是一种巧合。