数据文件流-基于风压谱的大跨度屋盖主体结构抗风设计理论

在抗风设计软件中，不论是与风荷载数据库发生大量的数据交换，还是在有限元分析时调用的质量、刚度矩阵及风荷载文件，都需要大量的数据传递。在数据传递过程中，如果格式不统一会造成程序无法正常运行，无法得到正确的结果。因此，有必要对数据格式进行统一约定。

7.2.2.1　风压统计量及频谱参数数据WLdata

风压统计量及频谱参数数据是软件中最为重要的数据，不仅是风荷载数据库中存储的数据，还是数据挖掘、风荷载随机模拟、风振响应分析、结果后处理模块中的风荷载输入参数，也是数据分析、预测分析模块的输出文件。风荷载统计量及频谱参数数据一般为32列，具体内容如表7-2所示。值得说明的是，该数据文件将尽可能全面的参数化统计信息和频谱参数纳入其中，考虑到主体结构、围护结构、疲劳分析涉及的参数，试图避免数据的重复分析。

表7-2　风压统计量及频谱参数数据文件格式

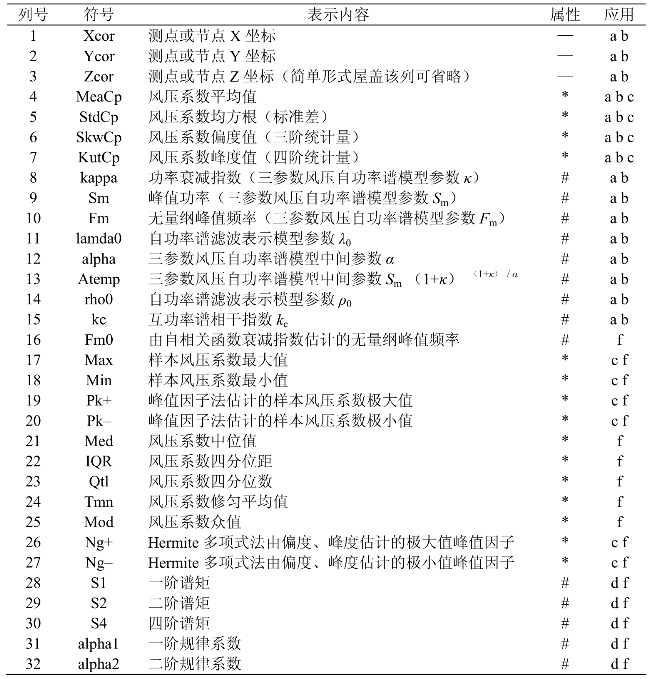
注：属性一栏中，*表示统计量，#表示频谱参数；应用一栏中，a表示风振响应分析，b表示随机模拟，c表示极值风压估计，d表示疲劳分析，f表示数据校验及其他分析。

表中1～3款为测点位置坐标；4～7款为风压系数的矩统计参数，按式（7-1）至式（7-4）对风压系数文件进行统计分析，得到屋盖上各点的风压系数平均值Cpmean、均方根CpRMS、偏度系数CpSkw和峰度系数CpKut。

表7-2中的8～16款为风压谱模型参数，按本书第3～4章的方法计算。表7-2中的17～18款为风压系数的最大值与最小值按式（7-5）和式（7-6）计算，

按式（7-7）和式（7-8）计算风压系数的极大值与极小值（峰值因法子）分别为表7-2中的19～20款，非高斯峰值因子为表7-2中的第26～27款，

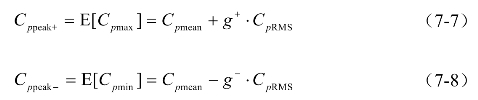
根据Hermite展开，非高斯峰值因子g表示为高斯峰值因子g0（±3.5）的多项式

按照屋盖结构风荷载规范[4]，

（1）当偏度系数CpSkw≥0，且峰度系数CpKut≥3时，取

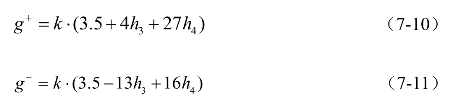
（2）当偏度系数CpSkw＜0，且峰度系数CpKut≥3时，取

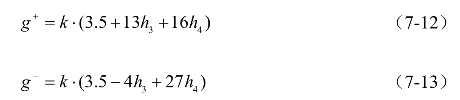
（3）当峰度系数CpKut＜3时，取

其中，

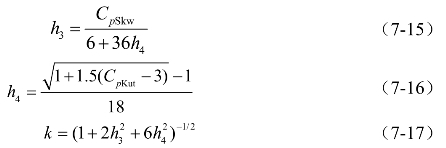
随着极值分析理论的发展，对于非高斯风压场极值估计更精细化的估计，陈新中等[81，208]提出了根据概率密度曲线（CDF）的转换函数估计方法，刘敏等[83，209-212]提出了分段Hermite函数（moment-based piecewise hermite polynomial model，PHPM）的转换函数估计方法，并改进了矩统计参数以适应强非高斯性；马兴亮等[213-214]提出了基于Johnson变换的方法，具体可参见相关文献。

表7-2中的21～25款为基于分位数的统计量。分位数的概念对于随机变量X，其容量为N的样本集{xi，i=1，2，…N}的p分位数xp定义为：

(www.xing528.com)

当p值为1/4的整数倍时，xp称为四分位数。

图7-3给出了基于分位数的盒装图，盒状图是数据分布特征的一种的统计图，通过数据的各四分位数直观反映出数据的分布状态（集中分散状态，分布的对称性），是一种“简易的”概率密度曲线。此外，盒状图能直观显示出“离群值”，即图中上下规格限以外的数据点，剔除了局部坏数据的干扰，更便于发现数据的整体规律。

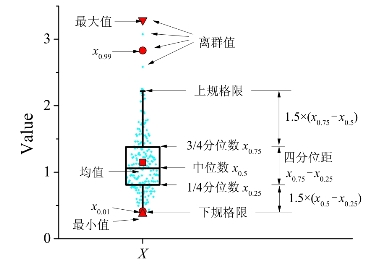
图7-3　盒状图示意图

上图给出了盒状图上特征点的概念示意图，后文盒状图采用与该图相同的标志。图中散点为某参数X的样本数据点，数据为服从参数为(0，0.4)的对数正态分布的200个随机数，本节后面内容以该组随机数为算例展开。为去除局部离群值的影响，去除上下1%的样本点，本文探讨参数的取值范围定义为x0.01～x0.99。四分位距IQR定义为，

频率直方图和概率密度曲线（PDF）是能够更加精细化反映数据分布特征的统计图，对于参数（或变量）X的样本集，首先进行分段，分段区间长度称为组距，经过统计计数得到各区间上的频数，以各区间中点值为横坐标，以频数÷样本容量÷组距为纵坐标的条形图称为频率直方图，频率直方图与横轴包围的面积为1。

理论上，若样本容量无限大，频率直方图的区间无限细分，频率直方图将收敛于概率密度曲线。但在样本容量有限的情况下，无法采用该方法获得概率密度曲线。在这种情况下，一般采用数值算法估计未知的概率密度，最常用的算法是核密度估计法。基本思想是对样本数据xi（i=1，2，…N）构造核函数K[（x-xi）/h]加权平均，得到较为光滑的概率密度曲线，见式（7-20）。

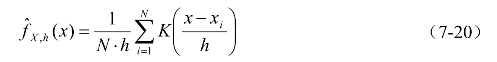
式中，对于核函数K（u）可取高斯函数，即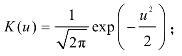h为核函数的带宽，根据拇指法则，由式（7-21）确定。

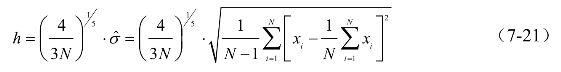
式中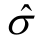，为样本集方差估计值。

参数（变量）X的众值Xmode定义为式，

众值表征样本集中出现最为频繁的值，即概率密度曲线最大值对应的数值，认为在样本数据集中最具代表性。本文在对参数进行分区值提取时，采用分区数据集的众值。当数据的概率密度中出现多个峰值（驻点）时，可根据实际情况对局部峰值进行提取。

图7-4中给出了对数正态样本X的盒状图、频率直方图，以及概率密度曲线、众值的理论与估计值。从盒状图中可以明显看出数据的分布状态明显呈现非对称分布状态，且数值大多数在1附近。通过频率直方图可看出各部分数值分布的情况，由于受到区间宽度的限制，只能得出众值的区间，采用本节方法计算的概率密度估计值与频率直方图分布接近，曲线更光滑，能够得到众值的估计值。虽然概率密度的估计值与理论值存在一定差距，但其与频率直方图更为接近，更能真实反映数据的实际分布特征，众值的估计值与理论值误差仅5.9%，说明纵使实际数据存在一定的离散性、与理论分布有一定差异，但通过本节方法分析数据的特征能够排除这种不确定性的干扰，得到数据的普遍规律。

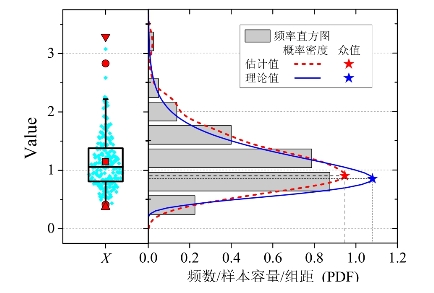
图7-4　盒状图、频率直方图、概率密度曲线与众值

此外，表7-2中的28～32款中的谱矩和规律系数可按公式（2-47）至式（2-49）进行求解。

7.2.2.2　有限元模型数据FEdata

在对结构进行风振响应分析时，需要将结构有限元模型中的信息提取，并将数据的格式进行统一，见表7-3。

表7-3　结构有限元模型数据文件列表

续表

注：*表示可由结构阻尼比计算，因此为备选项；#表示可由模态分析得到，或者直接输入，代替质量、刚度矩阵；ND为自由度数，NL为加载节点数，NN为节点总数，NRA为考察的轴力响应数量，NRR为考察的支座反力数。