背景和共振效应系数范围

基于上一节的背景、共振效应系数（μc、μd）的影响因素分析结果，本节将针对其主要影响因素综合对比，考察不同屋盖形式的背景、共振效应系数（μc、μd）取值范围。其中，共振效应系数μd为了排除阻尼比ζn的影响，主要考察共振能量因子SE随频率比fn/fm的曲线。

6.2.3.1　背景效应系数μc

对于背景效应系数μc，主要考察屋盖矢跨比、结构形式的影响，对全部工况的背景效应系数μc范围统计如图6-12所示。由图可以发现，单层网壳结构的背景效应系数μc绝大多数情况均大于1，远超过同矢跨比的双层网壳结构。对于单层网壳结构，随着矢跨比的减小，网壳趋于扁平，背景效应系数呈现明显的增大趋势；而多数双层网壳结构的背景效应系数μc小于1，尤其是当矢跨比变小时，双层网壳有趋向平板网架的趋势。总体看来，双层网壳结构背景效应系数μc随矢跨比并不是单调变化，而是以先增大后减小的趋势在1/4矢跨比附近达到峰值。当上一节按照屋盖形式分析时，矢跨比的影响被屋盖形式的影响掩盖，尤其是当矢跨比较小时，单层网壳和双层网壳的趋势可能相反，互相抵消。

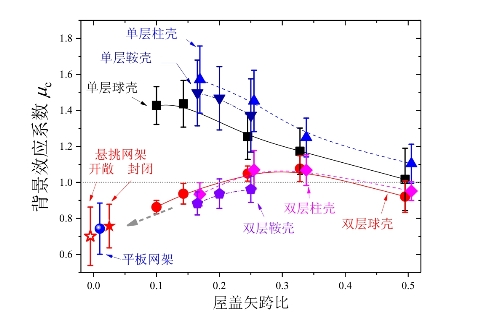
图6-12　全部计算工况背景效应系数随屋盖矢跨比的变化

从网壳形状看来，对于单层网壳结构，背景效应从大到小依次为柱面网壳＞鞍形网壳＞球面网壳；对于双层网壳结构，即柱面网壳≈球面网壳＞鞍形网壳。此外，还发现平板网架与悬挑网架的背景效应系数取值较为接近，虽然悬挑网架看台开敞情况对背景效应系数有一定影响，看台封闭屋盖略大于看台开敞的情况，经统计分析发现与平板网架无显著性差异，可进行统一。

总体看来，背景效应系数μc取值范围可归纳为：平板网架及悬挑网架结构(0.55，0.90)；对于双层网壳结构，小矢跨比（小于1/4）为(0.80，1.00)，中等矢跨比（1/4～1/3）为(0.90，1.15)，大矢跨比（1/3～1/2）为(0.85，1.05)；对于双层网壳结构，小矢跨比（小于1/4）为(1.30，1.70)，大矢跨比（1/3～1/2）为(0.90，1.30)，中等矢跨比介于其间，且柱面屋盖偏向上限值，球面屋盖偏向下限值，鞍形屋盖介于其间。(www.xing528.com)

6.2.3.2　共振能量因子SE

为综合考虑阻尼比ζn的影响，将共振效应系数μd转化为共振能量因子SE，给出全部工况下共振能量因子μd随频率比fn/fm的变化曲线如图6-13所示。由图可以发现，针对每种屋盖形式，共振能量因子SE随频率比fn/fm在对数坐标下均接近直线，印证了参数分析中二者Spearman秩相关系数极高的结果，也说明可以用幂函数的形式拟合该曲线。

图6-13　全部计算工况共振能量因子随频率比的变化

针对不同结构形式还可以发现，共振能量因子SE总体趋势为单层网壳＞双层网壳＞网架结构。对比各类结构的风振特性可以发现，这个顺序与结构高阶模态参与振动的程度极为接近，单层网壳结构的高阶模态贡献最为显著，模态耦合效应也极为明显，使得结构对风荷载的动力效应较为敏感，共振能量由多阶模态共同提供。其次是双层网壳结构，虽然没有特高阶模态的参与，但结构的前十几到几十阶模态作用较大。最后是平板网架及悬挑网架结构，这类结构的风致振动最多由前三到五阶模态主导，共振能量因子SE较低。

将各类结构形式的共振能量因子SE按式（5-27）进行幂函数拟合，首先通过统计双对数坐标下曲线的斜率发现其指数参数η2均接近2.0，与结构形式无关。在此基础上对系数项参数进行η1拟合并统计。统计结果显示，η1的取值范围为：对于网架结构，取(0.38，1.06)；对于双层网壳结构，取(0.94，2.08)；对于单层网壳结构，取(2.04 5.12)。