本节将第4章的算例进行拓展,采用阵风响应包络法分别对不同自振频率、阻尼比的大跨度悬挑网架及单层球面网壳进行等效风荷载分析,并将分析结果与前文简化模型理论推导的概念性规律进行对比,验证方法的有效性。
为了探讨背景及共振效应系数在实际三维大跨度屋盖结构中的意义及分布规律。本节选取的两种典型大跨度屋盖结构形式,一种是“同号”模态占主导地位的悬挑网架,另一种是“变号”模态占主导地位的单层球面网壳,根据5.3.1和5.3.2节的概念分析可知,这两种结构形式将产生不同形式的背景效应。此外,本节将4.4节的算例进行拓展,考察了不同的结构频率和阻尼比,旨在考察共振效应的变化规律,为第6章中的参数化分析奠定基础。
有限元模型的几何尺寸和结构形式与4.4节一致,通过调整杆件截面尺寸和屋盖表面的等效质量,得到不同自振频率的结构,每个结构都采用瑞利(Reyleigh)比例阻尼,阻尼比考察0.01、0.02、0.05三种。荷载工况采用3.1.1节表3-2的相应工况信息。计算模型信息见表5-1。
表5-1 计算模型信息

按照第4章的风振响应计算方法对上述大跨度屋盖结构进行风振响应频域分析,得到动力风振响应均方根(下文简称动力响应)。采用5.2.1节中的方法对结构进行准静力分析和静力分析,得到结构的背景效应和基准响应。图5-8给出了典型工况的动力响应、背景响应和基准响应。其中,悬挑网架为看台封闭的最不利工况,风向为30°。图5-8a、b分别是不同自振频率下的结果,由图可以看出,基准响应、背景响应和动力响应的分布规律基本一致,且背景响应小于基准响应,这是由于悬挑网架的一阶模态为“同号”模态(图4-11b),风荷载的部分相关性对结构响应是折减作用;随着结构频率的增大,动力响应与背景响应的相对比值降低,使得动力响应趋于背景响应。对于图5-8c、d的1/3矢跨比、1/2高跨比单层球面网壳来说,基准响应则略小于背景响应,这是由于该结构的一阶模态为“变号”模态(图4-11c),部分相关荷载对结构有一种放大效应。
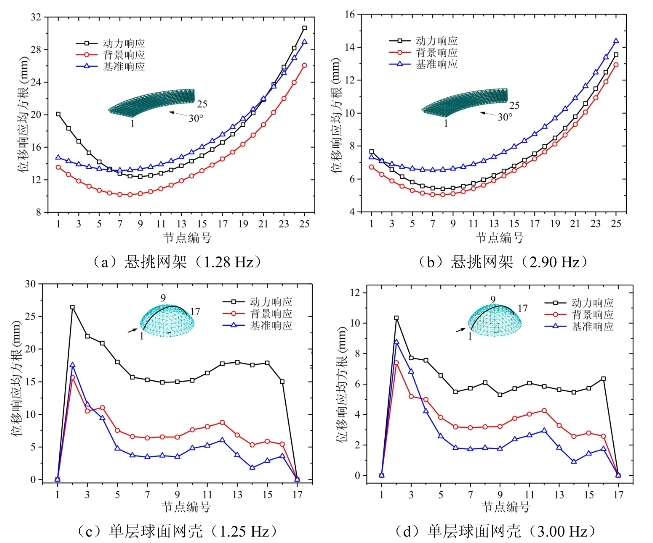
图5-8 典型工况位移响应均方根值(ζn=0.02)
基于背景、共振效应系数的定义式(5-7),得到各工况下μc、μd随自振频率和阻尼比的变化如图5-9所示。由图可以发现,对于相同类型结构,在同一种风荷载工况作用下,背景效应系数μc并不随结构频率、阻尼比变化而改变,理论上背景效应系数μc仅反映了风荷载在结构上的准静力效应,与结构动力效应参数——结构频率及阻尼比无关。但结构形式和风荷载工况对背景效应系数μc影响较为明显,尤其是结构形式主要决定了部分相关性风荷载的放大或折减效应,而风荷载自功率谱特征参数——峰值频率fm、互功率谱特征参数——相干指数kc的取值主要取决于风荷载工况。(https://www.xing528.com)
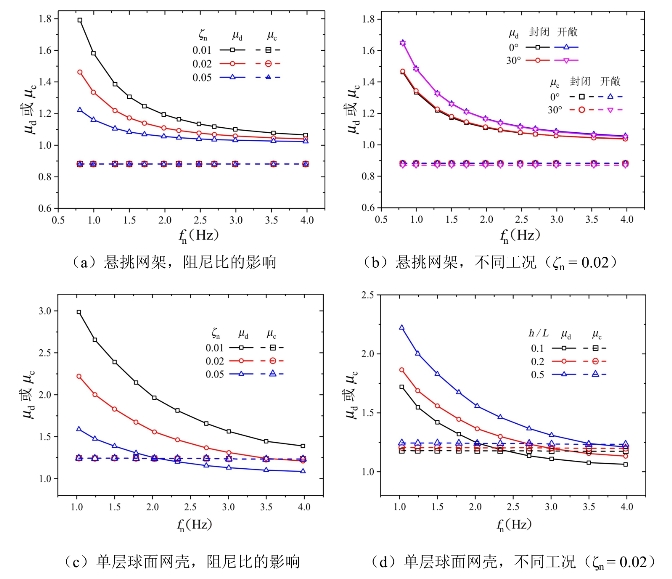
图5-9 各工况背景、共振效应系数计算结果
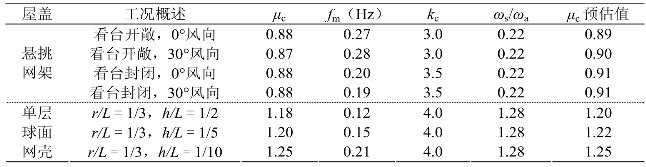
表5-2给出了各工况背景效应系数μc及其相关参数,并给出了按式(5-20)的预估值,可见预估值与计算值吻合较好,验证了前文的概念分析的正确性。至于共振效应系数μd,不言自明地受结构频率、阻尼比影响较为明显。此外,风荷载工况也对结果具有影响,一方面在于不同风荷载工况下的风荷载峰值频率不同,使得不同工况共振效应系数曲线随自振频率的衰减有所差异;另一方面,多自由度结构的风振响应主要体现在模态力上,互功率谱往往对模态力谱在高频衰减的影响较为显著,针对复杂的大跨度屋盖结构还需要考虑模态耦合的影响,情况更为复杂,主要体现在不同结构形式的风致共振特性差异较大。
表5-2 各工况背景效应系数及其预估值
考虑阻尼比的影响,将共振效应系数μd采用式(5-27)转化为共振能量因子SE,再将结构频率与各工况风荷载峰值频率的比值作为横坐标,得到SE-fn/fm曲线如图5-10所示。在双对数坐标下可以看出,在相同的结构形式下,SE仅与频率比相关,阻尼比基本无影响,且SE与fn/fm基本呈直线,说明采用式(5-27)的指数函数形式近似该曲线是一种合理的简化。本章算例结果拟合曲线见图5-10,由图还可以看出,两种屋盖结构SE-fn/fm曲线的衰减斜率(指数η2)较为接近,单层球面网壳的共振能量因子整体高于悬挑网架结构,这种现象将在第6章中的参数分析中具体讨论。
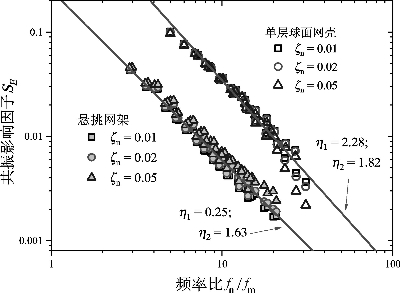
图5-10 各共振能量因子计算及拟合结果
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




